拉普拉斯定理及证明？

Posted 2023-03-18

麻烦详细点。。

设B是一个

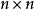
 的矩阵，

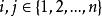
 为了明确起见，将

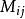
 的系数记为

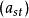
 其中

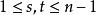
考虑B的行列式|B|中的每个含有

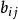
 的项，它的形式为：

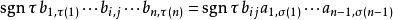
其中的置换τ ∈Sn使得τ(i) =j，而σ ∈Sn-1是唯一的将除了i以外的其他元素都映射到与τ相同的像上去的置换。显然，每个τ都对应着唯一的σ，每一个σ也对应着唯一的τ。因此我们创建了Sn−1与τ∈Sn:τ(i)=j之间的一个双射。置换τ可以经过如下方式从σ得到：

定义σ' ∈Sn使得对于1 ≤k≤n−1，σ'(k) = σ(k)并且σ'(n) =n，于是sgnσ' = sgn σ。然后

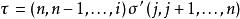
由于两个轮换分别可以被写成

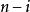
 和

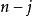
 个对换，因此

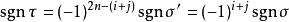
因此映射σ ↔ τ是双射。由此：

 

 

 

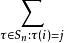
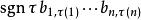
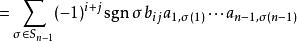
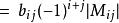
从而拉普拉斯展开成立。

扩展资料：

拉普拉斯定理

拉普拉斯在1772年的论文中给出了行列式展开的一般形式，称为拉普拉斯定理。拉普拉斯定理建立在子式和余子式的基础上，说明了如果将B关于某k行的每一个子式和对应的代数余子式的乘积加起来，那么得到的仍然是B的行列式。

定理的证明与按一行（一列）展开的情况一样，都是通过建立置换间的双射来证明两者相等。

参考技术A 第八章 拉普拉斯变换
基本要求：
1. 掌握拉普拉斯变换的基本概念以及常见函数的拉普拉斯正变换；
2. 利用拉普拉斯变换的基本定理，拉普拉斯变换表以及部分分式展开法对常见函数进行拉普拉斯反变换；
3. 利用拉普拉斯正反变换求解线性动态电路的常微分方程。

引言：所谓复频域分析，是指线性动态电路的一种分析方法，这种方法不是在时间域里直接进行分析和求解，而是变换到复频域的范围内求解。所使用的教学工具就是拉普拉斯变换.拉普拉斯变换是一种积分变换，是解线性常微分方程，研究线性系统的一个重要工具。下面回顾“变换”的概念。

1、对数与指数的变换
为求乘积ab
可先取对数 ln(ab)= lna+lnb
再取指数运算
2、相量与正弦量的变换
为了计算正弦稳态响应，可将激励源变为相量，然后在频率域里求相量（即相量法），然后再变回时域得到正弦时间函数响应。

其中 此复数的模 就是正弦量u(t)的振幅值，幅角就是u(t)的初相角。这种对应关系就是一种变换。

§8-1 拉普拉斯变换
讲述要点：1. 拉普拉斯变换的定义
2.常见函数的拉普拉斯变换

一．拉普拉斯变换
定义式：设有一时间函数f(t) [0,∞] 或 0≤t≤∞单边函数

其中，S=σ+jω 是复参变量，称为复频率。
左端的定积分称为拉普拉斯积分，又称为f(t)的拉普拉斯变换；
右端的F(S)是拉普拉斯积分的结果，此积分把时域中的单边函数f(t)变换为以复频率S为自变量的复频域函数F(S)，称为f(t)的拉普拉斯象函数。
以上的拉普拉斯变换是对单边函数的拉普拉斯变换，称为单边拉普拉斯变换。
如f(t)是定义在整个时间轴上的函数，可将其乘以单位阶跃函数，即变为f(t)ε（t），则拉普拉斯变换为

其中积分下标取0-而不是0或0+ ，是为了将冲激函数δ(t)及其导函数纳入拉普拉斯变换的范围。

二．拉普拉斯反变换

这是复变函数的积分
拉氏变换和拉氏反变换可简记如下
F(S)=L[f(t)] ； f(t)=L-1[F(s)]

三．拉氏变换的收敛域：
例8-1-1 单边指数函数 （其中a为复常数）

当 ＞0时，结果为有限值即

具体的说,即Re[s]- Re[a]=σ- Re[a] > 0 有σ> Re[a]这时eatε(t)的拉氏变换存在。我们称σ> Re[a]的s=σ+jω的范围为该函数的拉氏变换的收敛域，一般而言，对一个具体的单边函数f(t)，并非所有的σ值都能使f(t)eσt绝对可积，即把能使用f(t)eσt绝对可积的s的范围称为单边函数f(t)的拉氏变换的收敛域。
收敛域可以在s平面上表示出来，如下图。

如前例变换的收敛域为:σ> Re[a]=σO

例8-1-2， 单位冲激函数δ(t)的象函数

收敛域为整个s平面

例8-1-3 单位阶跃函数ε（t）的象函数

收敛域σ>0 , 右半s平面

§8-2 拉普拉斯变换的基本性质
讲述要点：微分定理，积分定理， 时域卷积定理

假定以下需进行拉氏变换的函数，其拉氏变换都存在
1、线性组合定理
L[af1(t)±bf2(t)]=aL[f1(t)]±b[f2(t)]
若干个原函数的线性组合的象函数，等于各个原函数的象函数的线性组合。
例8-2-1 求sinωtε(t)的象函数

同理可得L[cosω(t)]=
此二函数的拉氏变换收敛域为 参考技术B 德莫弗-拉普拉斯定理

设在独立试验重复序列中，事件A在各次试验中发生的概率为p(0<p<1),随机变量ηn表示事件A在n次试验中发生的次数，则有.

其中z为任意实数，q=1-p.

证： 设随机变量ξi表示事件A在第i次试验中发生的次数(i=1,2,…,n,…)，则ξi服从“0-1”分布， 相互独立，且有

直接由列维定理就得此定理.

近似公式

在上述定理条件下，当n充分大时，ηn落在m1与m2之间的概率

（5.19）

注：此定理实际上说明了当n充分大时，二项分布B(n,p)逼近正态分布N(np,npq)，这是因为ηn是服从二项分布B(n,p)的. 参考技术C dF=-P1dVl-P0dVg+γdA=0
dVl=-dVg Pl-P0=γdA/dVl
△P=γd(4paiR平方)/三分之四πR立方=2γ/R