卷积神经网络学习笔记

Posted 2023-02-23 Maggie张张

一、理解卷积
首先，卷积是一种数学运算，从二维离散的卷积操作来理解这种运算的意义。摆出二维离散卷积公式：

$$C(x,y)=\\sum_-\\infty ^\\infty \\sum_-\\infty^\\inftyF(s,t)*C(x-s,y-t)$$
C(x,y)表示一个二维矩阵的函数值，C(x-s,y-t)是距离中心点(x,y)的函数值，F(s,t)是一个加权矩阵，对于中心点周围所有的点乘以一个加权值然后求和，就是该点新的函数值。举个例子：

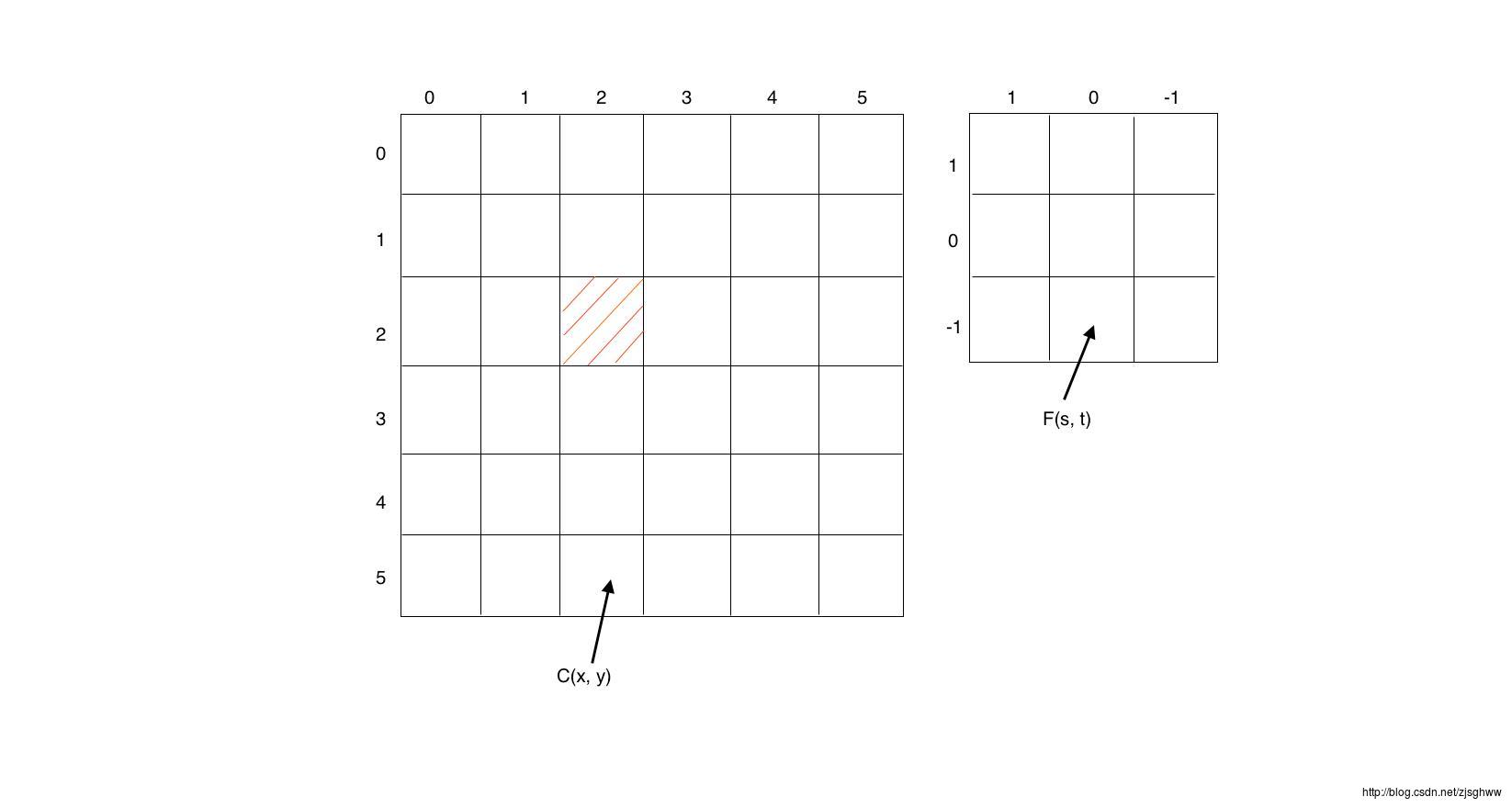
要求C(2, 2)新的值，对于F(s, t)函数， $t\\in \\left \\ -1,0,1 \\right \\$, 所以C(2,2)=F(-1,-1)C(3,3)+F(-1,0)C(3,2)+F(-1,1)C(3,1)+F(0,-1)C(2,3)+F(0,0)C(2,2)+F(0,1)C(2,1)+F(1,-1)C(1,3)+F(1,0)C(1,2)+F(1,1)C(1,1)， 对每个C(x,y)都进行这样的操作，可以把F矩阵看作一个概率密度函数，C函数的值进过F函数变换之后，又得到了一个新的C函数。
比如现在C函数值是一张图片(lena)组成的二维矩阵(512*512)，把它经过”suanzi”这个卷积核处理之后可以得到一个新的图像

from PIL import Image
import numpy as np
import matplotlib.pyplot as plt

def imconv(image_array, suanzi):
    image = image_array.copy()
    dim1, dim2 = image.shape
    for i in range(1, dim1-1):
        for j in range(1, dim2-1):
            image[i,j] = (image_array[(i-1):(i+2),(j-1):(j+2)]*suanzi).sum()
    #归一化
    image = image * (255.0/np.amax(image))
    return image

suanzi = np.array([[-1, 0, 1],
                     [-2, 0, 2],
                     [-1, 0, 1]])

image = Image.open("lena_std.tif").convert("L")
image_array = np.array(image)
image2 = imconv(image_array, suanzi)
plt.subplot(2,1,1)
plt.imshow(image_array,cmap="gray")
plt.axis("off")
plt.subplot(2,1,2)
plt.imshow(image2,cmap="gray")
plt.axis("off")
plt.show()

可以看到经过卷积之后的图片相当于做了一个滤波，适当的卷积核可以得到不同的信息，比如边缘信息等等。
引用一种比较简单的定义描述卷积：

卷积的目的就是将卷积核（滤波器）应用到某个矩阵的所有点上，并通过将卷积核在输入矩阵上滑动而产生经过滤波处理的矩阵。

二、从传统的神经网络到卷积神经网络
现在，理解一下为什么要用卷积神经网络处理图像。
（1）局部感知减少参数数量
比如一个传统的全连接神经网络拿这张lena图作为输入，相当于输入是512*512的一个二维向量，这个网络没有隐层，输出也是512*512的二维向量。那么他需要的参数数量是512*512*512*512。但是实际上，作为一张图片，相邻的像素点的信息十分相近，并不需要对网络进行全联接。而卷积操作就可以明显的对连接稀疏化，减少参数的数量。在输入层和输出层之间加一个卷积层，用一个3*3的卷积核跟输入层的每一个神经元连接（局部感知），可以得到的参数数量是512*512*3*3，明显地降低了参数的数目。
（2）参数共享
之前说用一个3*3的卷积核去作用于512*512个神经元，此时可能每个3*3的核的值都是不一样的，即他们依赖于不同的神经元，但是如果对每个神经元用一样的3*3的核，那参数的数量就只有3*3啦！这样做为什么可以呢？卷积相当于一个滤波，对每个神经元进行同样的过滤我们就可以只得到我们想要的信息（根据卷积核的自身特性）。这个信息就表达了图像的一个方面的特征，那么用不同的卷积核去作用于各个神经元，就可以提取到很多个不同的特征了。
（3）池化
依然对于我们这个512*512的输入，定义卷积核的大小是3*3，一个卷积之后得到一个（512-3+1)*(512-3+1)=260100维的特征，10个卷积核得到2601000维的特征。这me庞大的特征集合放到一个分类器里面去容易造成过拟合。另外，图片本身只有局部性的，相邻像素比较相近，那么可以把学习到的特征一块一块地聚合一下（求平均或者求最大值等），这样得到的特征集合又进行了一次稀疏化。这个过程就叫做池化。

基于卷积给神经网络带来的这些好处，尤其是在处理图像的场合，所以卷积神经网络在图像处理领域才能发展的这么好吧。

三、卷积神经网络——把卷积操作加到神经网络里面去
以经典的LeNet5结构来理解：

（1）输入层：32*32的矩阵
（2）C1卷积层：选取6个3*3的卷积核学习6个特征，每个特征(32-3+1)*(32-3+1)维，特征集合6@28*28
（3）S2池化层：每个特征slice池化的块的大小为15*15，对块中的数值进行聚合（求平均或取最大），特征slice变成(28-15+1)*(28-15+1)， 特征集合变成6@14*14
（4）C3卷积层：选取16个5*5的卷积核，特征集合变成16@10*10
（5）S4池化层：池化块大小6*6，特征集合变成16@5*5
（6）C5隐层：120个神经元，与S4中的16@5*5个神经元全联接
（7）F6隐层：84个神经元，与C5中的所有神经元全联接
（8）输出层，10个神经元，与F6的神经元高斯连接，实际上这一步有一个分类器。

那么，CNN的结构通常就是这样：输入层+卷积层+修正层+池化层+全联接层+分类层。

通常实际问题中，卷积层和池化层（成对出现）的数目和结构（即卷积核和池化块的大小）按照需求设定，所有参数按照前向传播算法（FP）和后向传播算法（BP）来学习。