车间调度基于matlab候鸟算法MBO求解柔性作业车间调度问题含Matlab源码 2354期

Posted 2023-02-22 海神之光

⛄一、车间调度简介

1 柔性作业车间调度问题
FJSP问题可描述为:车间内n个工件在m台机器上加工.各工件均包含一道或多道工序,同工件各工序间存在固定的加工顺序.工序可在多于一台的机器上加工,其加工时间与所在机器有关.FJSP问题优化的目标是为工序分配适当的机器,排列各机器上工序间的加工顺序并计算其开始/完工时间,最终使系统某个或某些性能达到最优[1].

对于这样的系统,存在一些基本的假设条件:
1)初始零时刻所有工件和机器都是可用的.
2)一台机器在某一时刻只允许加工一个工件.
3)各工序的加工过程一旦开始不允许被中断.
4)同工件工序间具有先后加工的约束关系,不同工件工序间则相互独立.
5)各工件具有相同的加工优先级.
6)忽略机器加工工序前所需的调整时间.
高效快速完成生产任务仍然是大多数企业追求的首要目标.因此,本文以最大完工时间Cmax作为优化目标,则目标函数可表示为

其中,Ci表示工件i的完工时间.

2 混合型候鸟迁徙优化算法
候鸟迁徙优化算法是一种新兴的邻域搜索技术,它通过模拟候鸟的自然迁徙行为来实现对目标的优化[10].整个算法分为算法初始化,领飞鸟进化,跟飞鸟进化和领飞鸟替换四个阶段.种群中所有个体构成V字形编队,由领飞鸟开始向队列两端通过搜索个体的邻域解进行进化,最终实现目标的优化.种群中的个体除了搜索自身邻域解进行更新外,还可以搜索其所在队列中前一个个体的邻域解(领飞鸟除外,只搜索自身邻域解).这种搜索机制能够提高算法找到更优解的概率,使算法能够快速地获得最优解,体现了算法的集中搜索能力[13].MBO算法比较适用于求解离散组合优化问题[13],因此,本文针对FJSP问题的特点采取一系列改进措施,使MBO算法能够更好地用于FJSP问题的求解.

2.1 编码/解码方案
由于求解FJSP问题主要是解决机器分配和工序排序两个子问题,因此种群中每个个体可分为两段表示,长度均为车间内的工序总数.前半段表示机器分配方案,后半段表示工序间排序方案,如图1所示.前半段中元素值为工序所在机器的编号,按固定顺序存储,如图1(a)所示;后半段中相同的元素值表示同一工件的不同工序,元素间的先后顺序表示工序间的加工顺序,如图1(b)所示.

解码时结合前后两段编码进行操作,从左到右依次读取后半段元素代表的工序,然后在前半段找到其对应的机器,并计算工序的开始和完工时间.

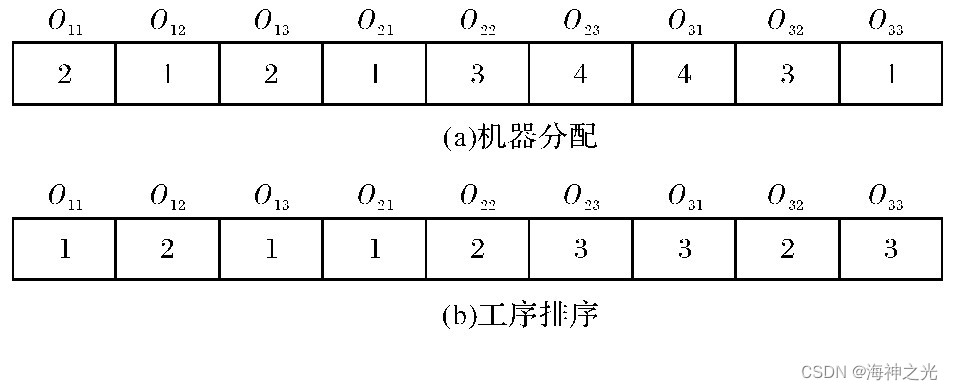
图1 编码方案

2.2 种群初始化方案
与其他群智能优化算法(如遗传算法和粒子群算法等)相同,候鸟迁徙优化算法的性能也在一定程度上受到种群初始解的影响.因此,设计一个好的种群初始化方案是必须要解决的问题.根据个体编码方式,初始种群可分两个阶段进行初始化,即机器分配阶段和工序排序阶段.

对于机器分配阶段,采用以下3种方法:
1)随机生成法:在每道工序可加工机器集内随机选择一台机器填入初始解的前半段.
2)全局搜索法:采用文献[2]中的全局搜索方法确定初始解前半段机器分配方案,使机器的工作负载平衡,提高机器的使用率,并同时考虑最小化最大完工时间.
3)局部搜索法:采用文献[2]中的局部搜索方法确定初始解前半段机器分配方案,其目的和全局搜索方法一样.
对于工序排序阶段,目前很多文献均采用随机生成法或根据调度规则生成初始排序方案[14,15].本文采用基于搜索的方法得到初始解的后半段.针对每一个已生成的机器分配方案,均采取以下操作:首先随机生成若干个工序排序方案,然后评估每个排序方案结合该机器分配方案后各自对应的目标值,选择其中最优的一组作为初始解.

2.3 邻域结构
候鸟迁徙优化算法中个体通过搜索自身以及排前一个个体的邻域解对问题的解空间进行搜索,以获取优化目标的最优值.因此,邻域解的构造直接影响着算法的求解质量和收敛速度.本文采用以下3种邻域结构,具体构造过程如下:
1)邻域结构N1:在调度解的工序排序部分任意选择两个位置,并将两位置间元素逆序排列.
2)邻域结构N2:在调度解的工序排序部分任意选择两道不同工件的工序,并互换两工序所在的位置.
3)邻域结构N3:在调度解的机器分配部分任意选择一道工序,并将其分配至可选机器集合中(不包括当前机器)加工时间最短的机器上.

2.4 重置机制
在算法中引入一种重置机制,以避免算法陷入局部最优解.具体做法为,首先为种群中每个个体均设置一个解龄.对于新产生的个体,其解龄为1,若经过一次进化后计算结果未发生变化的个体,其解龄加1.若某个个体的解龄超过了预定的上限limit,则对该个体进行重置操作,即采用上述全局搜索法和基于搜索的方法重新生成一个新个体替代原来的个体.

2.5 变邻域搜索
基于上述3种邻域结构设计一种变邻域搜索算法嵌入到候鸟迁徙优化算法中,并作用于当前最优个体,以加强算法的局部搜索能力.
变邻域搜索算法的具体步骤如下:
步骤1:算法初始化.将候鸟迁徙优化算法得到的当前最优解作为变邻域搜索算法的初始解 π,设置qmax←3,it←1及最大循环次数itmax.
步骤2:设置q←1.
步骤3:振动环节.若q=1,则按邻域结构N1和N3对π进行变换得到新解π′;若q=2,则按邻域结构N2和N3对π进行变换得到新解π′;若q=3,则按邻域结构N3对π进行变换得到新解π′.
步骤4:局部搜索.以振动环节得到的π′ 作为局部搜索的初始解,找到局部最优解π″.
步骤5:若π″优于π,则π←π″,并设置q←1;否则,设置q←q+1.
步骤6:判断q>qmax是否成立.若是,设置it←it+1,执行步骤7;否则,转到步骤3.
步骤7:判断it>itmax是否成立.若是,执行步骤8;否则,转到步骤2.
步骤8:变邻域搜索结束.

变邻域搜索算法中局部搜索的具体步骤如下:
步骤1:获取初始解π′,并设置lmax← 3,λ←1和最大循环次数λmax.
步骤2:设置πL.

⛄二、部分源代码

clc;clear
%% 下载数据
% 加工数据包括加工时间，加工机器，机器数，各机器权重，工件数，各工件对应的工序数
load data operation_time operation_machine num_machine machine_weight num_job num_op

%% 基本参数
MAXGEN=200; % 最大迭代次数
sizepop=201; % 种群规模
e=0.5; % 目标值权重
N_size=30; % 邻域解数量
S_size=15; % 共享解数量
G=5; % 巡回次数
G1=20; % 竞争机制1参数
G2=10; % 竞争机制2参数
trace=zeros(2,MAXGEN);
chrom_best=[];

%% =种群初始化==
total_op_num=sum(num_op);
chroms=initialization(num_op,num_job,total_op_num,sizepop,operation_machine,operation_time);
[Z,_,,_,]=fitness(chroms,num_machine,e,num_job,num_op);
% 将最好的解划分为领飞鸟
[Z_leader,ind]=min(Z);
leader=chroms(ind,:);
% 从chroms中移出领飞鸟，然后划分左右两个跟飞鸟种群
chroms(ind,:)=[];
Z(ind)=[];
sp=(sizepop-1)/2;
lefts=chroms(1:sp,:);
Z_left=Z(1:sp);
rights=chroms(sp+1:end,:);
Z_right=Z(sp+1:end);

%% 迭代过程=
for gen=1:MAXGEN
fprintf(‘当前迭代次数：’),disp(gen)
%% 巡回阶段
for i=1:G
%% 领飞鸟进化
[leader,Z_leader,share,Z_share]=bird_evolution(leader,Z_leader,[],[],…
N_size,S_size,total_op_num,num_machine,e,num_job,num_op);
%% 跟飞鸟进化
% 初始化左右队列的共享解集
share_left=share;
Z_share_left=Z_share;
share_right=share;
Z_share_right=Z_share;
for j=1:sp
% 左队列
[lefts(j,:),Z_left(j),share_left,Z_share_left]=bird_evolution(lefts(j,:),Z_left(j),share_left,Z_share_left,…
N_size-S_size,S_size,total_op_num,num_machine,e,num_job,num_op);
% 右队列
[rights(j,:),Z_right(j),share_right,Z_share_right]=bird_evolution(rights(j,:),Z_right(j),share_right,Z_share_right,…
N_size-S_size,S_size,total_op_num,num_machine,e,num_job,num_op);
end
%% 竞争机制2：队间交叉
% 随机产生G2对位置相同的个体
ind=randperm(sp,G2);
[rights(ind,:),Z_right(ind),lefts(ind,:),Z_left(ind)]= crossover(lefts(ind,:),rights(ind,:),…
Z_left(ind),Z_right(ind),total_op_num,num_machine,e,num_job,num_op);
end
%% 竞争机制1：队内竞争
ind=randperm(sp,G1);
% 左队列
[~,ind1]=sort(Z_left(ind));
lefts(ind,:)=lefts(ind(ind1)😅;
Z_left(ind)=Z_left(ind(ind1));
% 右队列
[~,ind2]=sort(Z_right(ind));
rights(ind,:)=rights(ind(ind2)😅;
Z_right(ind)=Z_right(ind(ind2));
%% 领飞鸟替换
if rand<0.5
% 选择左队列首只跟飞鸟
[leader,Z_leader,lefts,Z_left]=update_leader(leader,Z_leader,lefts,Z_left);
else
% 选择右队列首只跟飞鸟
[leader,Z_leader,rights,Z_right]=update_leader(leader,Z_leader,rights,Z_right);
end

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]姚妮.混合候鸟迁徙优化算法求解柔性作业车间调度问题[J].华中师范大学学报(自然科学版). 2016,50(01)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除