配送路径规划基于matlab遗传算法连锁超市配送路线规划含Matlab源码 2347期

Posted 2023-02-22 海神之光

⛄一、基于计算机视觉的图像拼接技术研究简介

配送是连锁超市经营中的一个重要环节,配送包括“配”和“送”2个内容,“配”即对货物进行合理分配,将其置于不同车辆,“送”即对配送路线进行合理规划,从而提高车辆的载重和空间利用率,进而节约配送成本,换言之即货物配载问题和车辆路径问题[1]。

车辆路径问题(VRP,vehicle routing problem)于1959年由Dantzig等[2]提出,它主要研究在满足约束条件下最佳的车辆行驶路线方案。货物配载问题的研究始于国外,自1939年(Kantorovich),1940年(Brook)开始[3],解决最大化载重和容积利用率使得配送成本降低的问题。将这2个问题之间的相关性考虑在内,同时进行优化,建立模型并设计算法进行求解,无论从理论上还是实际上都有一定的意义。从理论上而言,可以丰富配送路线规划理论,从实际上而言,能够优化配送过程中资源利用不合理的问题[4,5,6,7,8]。

1 模型描述
研究配送路线优化问题的范围是:单个配送中心、多辆车辆、多品种货物、路网非对称、路线闭合型货物配装与车辆路径优化问题。

该模型可描述为从配送中心出发,由n辆车辆完成对多个客户点的配送,配送中心与客户的距离以及任意2个客户之间的路网距离已知,客户所需求的货物品种规格数量已知,所用车辆的载重和容积已知,车辆有最大行驶距离限制,在多个约束条件下,要确定车辆载重和容积利用率最大、投入使用车辆最少以及车辆总行驶距离最短的配送方案。

1.1 模型假设
综合优化模型在以下假设下建立:①配送为闭合的,且货物单向流动;②车辆为一对多个客户,每辆车1条线路;③各个客户的需求已知,货物为纸箱式包装;④货物在车厢内可以任意摆放。

1.2 模型参数及变量定义
对模型中的参数和变量定义如下:k表示车辆编号(k=1,2,…,n);i,j表示客户编号(i,j=0,1,2,…,n),i,j=0表示配送中心;p表示货物编号(p=1,2,…,m);uij表示客户点i,j之间的距离;Gk表示车辆k的额定载重量;vk表示车辆k的额定容积;gip表示客户i的货物p的重量;vip表示客户i的货物p的体积。

模型中涉及到的变量定义如下:

1.3 模型构建
结合模型描述、模型假设以及参数和变量定义,建立配送路线优化模型为



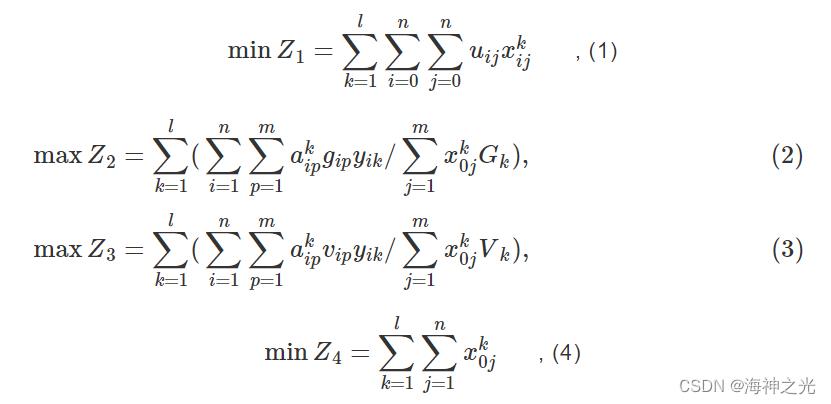
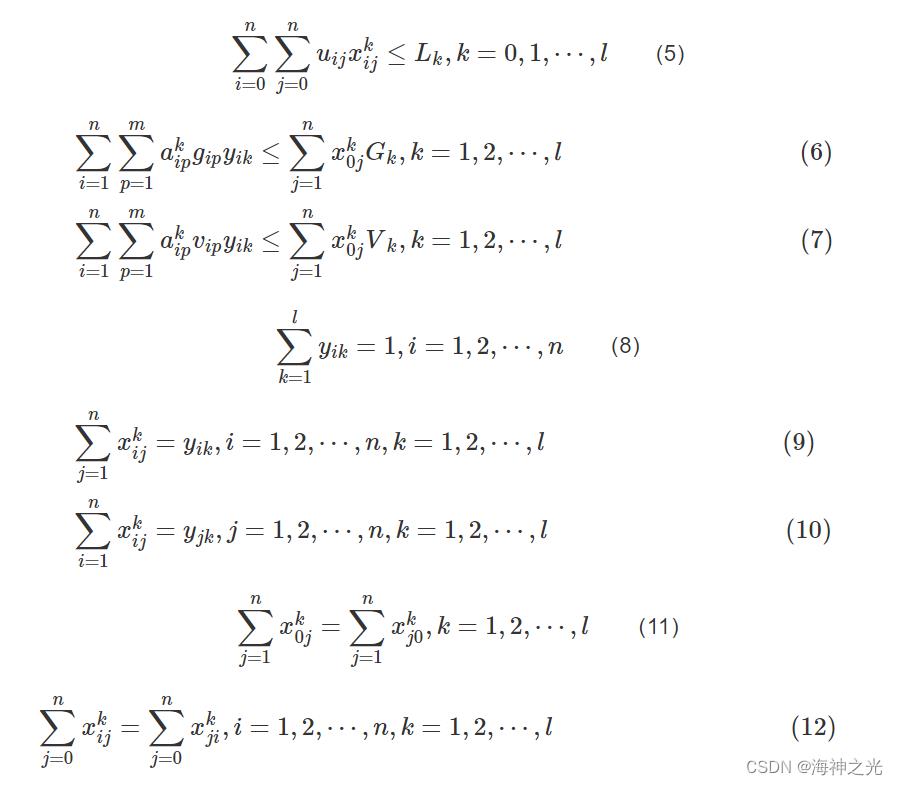
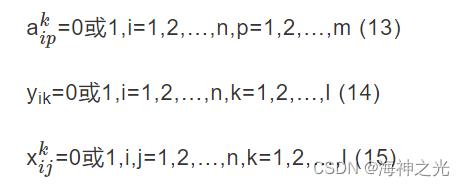
对模型目标函数解释如下:式(1)表示车辆总行驶里程最短;式(2)表示最大化载重利用率;式(3)表示最大化容积利用率;式(4)表示车辆使用数量最少;式(5)表示车辆最大行驶距离限制;式(6)表示车辆载重量限制;式(7)表示车辆装载容积限制;式(8)表示单个客户点货物应装载在同一辆车上;式(9)、式(10)表示每个客户只能由1辆车提供服务;式(11)表示车辆从配送中心出发最后返回配送中心;式(12)表示到达客户点i的车辆数与从客户点i开出的车辆数一致。式(13)～(15)为决策变量的0、1约束。

1.4 目标函数处理
上述模型存在多个目标函数,考虑到求解的复杂度,将多目标函数经过统一量纲处理转换成单目标函数,各个目标转换成成本函数后再进行相加,使得模型的求解结果以配送成本进行更为直观的反应。目标函数与成本的转换如图1所示。

2 改进遗传算法求解
基于基本的遗传算法[3,4,5,6]改进求解上述模型,具体的步骤如下。

2.1 整数编码
上述配送线路规划问题是带有车辆运行和货物装载访问次序的问题,0-1编码无法反映这一特征,因此考虑采用整数编码。编码思路如下:把所有客户点当作染色体中的各个基因,基因的排列顺序即代表车辆访问客户点和客户点货物装载的顺序。以某配送中心配送路线规划为例,假设该配送中心安排3辆车出发对10个客户点进行配送,共规划了3条配送路线:路径1:0-5-2-9-0,路径2:0-4-3-6-1-0,路径3:0-7-8-10-0。那么对于第1条配送路线而言,车辆配送客户的顺序即访问顺序为5,2,9,而对应的货物装载顺序为9,2,5。

2.2 产生初始化种群
在编码中随机生成了1×10染色体,并重复N次(N为初始种群的规模),把中间第i次生成的染色体放到一个规模为N×L种群的第i行,那么结果能带到含有N个个体规模的初始种群。

2.3 解码方案及适应值函数确定
采用对染色体从第1列开始进行累加求和的方式,计算对应客户点货物体积和重量的累加和,若到某个位置重量或容积累加和超过车辆额定载重或额定容积,则在该点后面插入0,若容积和载重累加和都未超过,那么计算出从配送中心到该列对应客户点,再从该点返回配送中心这条路线的总距离,判断是否超过车辆总行驶距离限制,若超过则在该位置插入0,再将货物总体积和总重量置为0,重复上述步骤,直至进行到最后一列染色体。

研究将目标函数的倒数定义为适应度函数,即fτ=1/f(pi)。

2.4 确定选择算子
采用轮盘赌和最优串选择相结合的方法选择算子,这种方法既能满足最优遗传,也能满足较优个体大概率遗传到下一代。

2.5 交叉算子
基于两点交叉算子对其进行改进,生成两点交叉变异算子,假设某个体有5个变量:设个体P1=1|24|53|,P2=3|51|24|,|为交叉点,子个体分别为C1和C2,取P2处2个交叉点中的基因放在子代C1对应位置处,而P2中交叉点[5,1]的补集[3,2,4]随机排列在C1其他位置,同理取P1交叉点中间的基因放在子代C2对应位置处,而P1中交叉点[2,4]的补集[1,5,3]则随机排列在子代C2其他位置。

2.6 变异算子
研究选取互换变异,将染色体其中2个地方的基因当作互换变异的点。

⛄二、部分源代码

clear
clc
%close all
%% 输入信息
data=load(‘data1.txt’);
% 配送中心位置
center_pos=data(1,2:3);
% 客户点信息
demand0=data(2:end,:);
demand=creat_demand(demand0);
para.vehicle_fix_cost=100;%车辆派遣费
para.vehicle_vel=60/60;%车辆行驶速度 单位km/min
para.vehicle_max_amount=100;%车辆最大服务能力
para.oil_fee_per_kilo=0.7;%配送车每公里油费
para.vehicle_maxnum=14;%车辆最大使用数目
%% 计算配送中心到客户点的距离
vertexs=[center_pos;demand.pos]; %所有点的坐标x和y
h=pdist(vertexs);
dist=squareform(h); %距离矩阵，满足三角关系，暂用距离表示花费c[i][j]=dist[i][j]
%% 遗传算法参数设置
NIND=300; %种群大小
MAXGEN=150; %迭代次数
Pc=0.9; %交叉概率
Pm=0.05; %变异概率
GGAP=0.9; %代沟(Generation gap)
N=demand.num+para.vehicle_maxnum-1; %染色体长度=需求点数目+备选中心数目-1
%% 初始化种群
rand(‘seed’,1);
Chrom=InitPopCW(NIND,N); %构造初始解
%% 遗传算法优化
gen=1;
figure;set(gcf,‘position’,[480 92 560 686]);
hold on;box on
xlim([0,MAXGEN])
ObjV=calObj1(Chrom,demand,para,dist); %计算种群目标函数值
preObjV=min(ObjV);
while gen<=MAXGEN
%% 计算适应度
ObjV=calObj1(Chrom,demand,para,dist);%计算种群目标函数值
subplot 211;
line([gen-1,gen],[preObjV,min(ObjV)]);drawnow;
title(‘优化过程’);
xlabel(‘代数’);
ylabel(‘最优值’);
preObjV=min(ObjV);
FitnV=Fitness(ObjV);
%% 选择
SelCh=Select(Chrom,FitnV,GGAP);
%% OX交叉操作
SelCh=Recombin(SelCh,Pc);
%% 变异
SelCh=Mutate(SelCh,Pm);
%% 重插入子代的新种群
Chrom=Reins(Chrom,SelCh,ObjV);
%% 删除种群中重复个体，并补齐删除的个体
Chrom=deal_Repeat(Chrom);
%% 打印当前最优解
ObjV=calObj1(Chrom,demand,para,dist); %计算种群目标函数值
[minObjV,minInd]=min(ObjV);
disp([‘第’,num2str(gen),‘代最优化值:’,num2str(minObjV)])
[bestVC,bestNV]=decode1(Chrom(minInd(1)😅,demand);
subplot 212;
draw_Best_iter(bestVC,bestNV,center_pos,demand,vertexs);
drawnow;
%% 更新迭代次数
gen=gen+1 ;
end

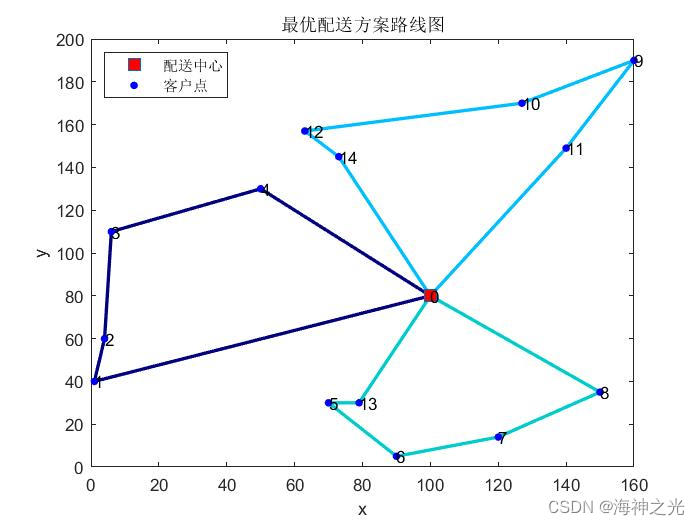
⛄三、运行结果

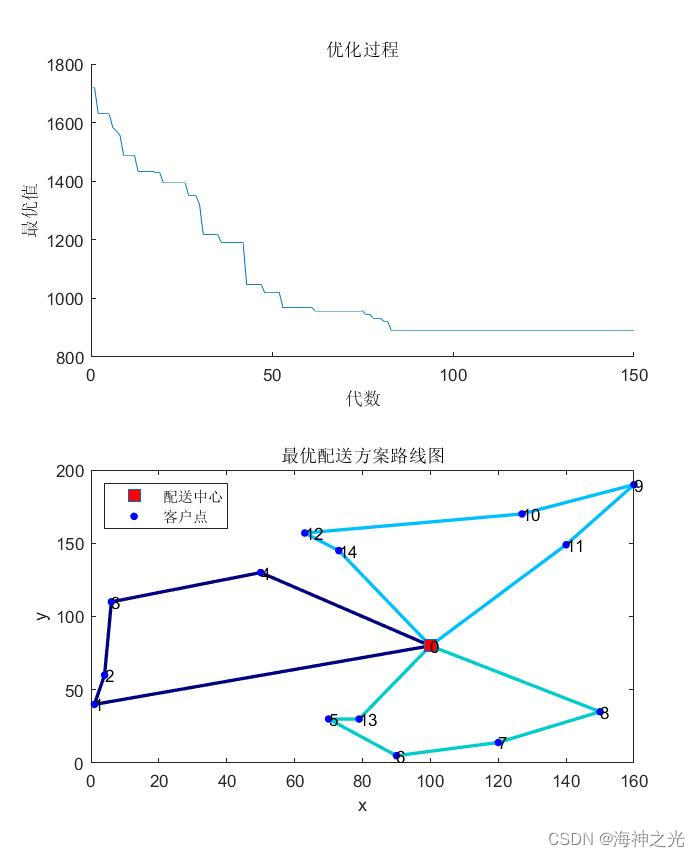
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]李小玲.基于改进遗传算法的连锁超市配送路线优化研究[J].甘肃科学学报. 2020,32(06)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除