12. 归纳偏好

Posted 2023-02-21 starrow

2.3 归纳偏好

 2.2节的成果令人振奋，因为回归和分类预测函数的表达式不仅精确，而且普适。然而，条件期望值或条件概率最大的类别仅有理论意义，而无法用于实际模型。以回归为例，在输出关于输入的条件概率分布未知的状况下，只能根据训练数据集来求输出条件期望的近似值，即对于某个待预测的输入值，在训练数据中找出所有具有同样输入的实例，取它们输出的平均值：

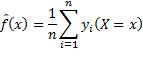
该方法的问题在于：首先，在训练数据中能找到多少输入相同的实例。这些实例的数目越大，其输出的平均值就越接近该输入处的输出期望值。可是训练数据不能保证在某个输入值处会有多少实例，若数量很少，其输出的平均值就可能和输出期望值相差甚远。其次，更严重的是，该方法只适用于训练数据所包含的输入值。对于训练数据未包含的输入值，无法求输出的平均值，而预测这些未知的输出，才是监督学习的目的和价值。总而言之，用输入相同实例输出的平均值作为预测，是一种吊诡的做法。在训练数据集内输入相同的实例越多处，预测越准确，而在该处已知的输出越多；在输入相同的实例越少处，预测越不准确，而在该处已知的输出越少；在训练数据集内无实例处，无法进行预测，而此处正是输出未知需要预测之处。对于分类，问题类似。

为了在训练数据未包含的输入处预测输出，需要更多信息，这样的信息只可能来自对模型所做的特定假设，即1.1.3节介绍的归纳偏好。有了某种偏好，f(x)的选择范围从所有函数缩小至某类型的、具有某特征的函数，虽然这些函数失去了通用性，只适用于解决特定问题，但能依据训练数据被求出。这种从一般到偏好，或通过特殊化或近似处理的方式解决实际问题的思路，在许多学科中都能见到。例如，古典经济学建立在理性人假设上，虽然现代经济学发现人的很多活动和决策是非理性的，但这并不妨碍在一定范围内由理性人假设推导出结论的有效性。再比如古典动力学对固体运动的研究建立在刚体概念的基础上，虽然现实世界并不存在真正的刚体，但古典动力学的结论在相当范围内，都可以作为足够好的近似应用于现实。某种意义上，在接触实际时带有某种偏好也可以作为人总是带着偏见看世界的隐喻（在英文中，归纳偏好中的偏好和偏见是同一单词Bias）。下面就循此思路，通过归纳偏好获取一个实用的模型。