matlab 矩阵内含未知数的计算问题
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了matlab 矩阵内含未知数的计算问题相关的知识,希望对你有一定的参考价值。
例如:K=[1 2 3;1 2 3;1 2 3] , Q=[0 q1 q2] ,F=[f1 0 0]
然后已知矩阵计算关系为 K*Q=F 怎么在matlab里面解q1 q2 f1。
谢谢
1、题目有点小问题——Q和F应该是列向量。
2、可以用fsolve求解:
>> K=[1 2 3;1 2 3;1 2 3];>> x=fsolve(@(x)K*[0 x(1) x(2)].'-[x(3) 0 0].',rand(1,3))
Optimization terminated: first-order optimality is less than options.TolFun.
x =
0.3051 -0.2034 0.0000
得到的x=[f1 q1 q2]。
3、上面求解方程组的初值随机生成,得到的结果也不一样,但可以检验:
>> K*[0 x(1) x(2)].'-[x(3) 0 0].'ans =
1.0e-006 *
-0.2258
0.1155
0.1155
在精度允许的范围内,都是满足方程的。由此可以判断,方程组属于欠定的,也就是说,方程组存在自由变量。
4、求解欠定方程组的通解有两种方法:
(1)把方程整理成Ax=b的形式,然后用null函数求零空间。
(2)使用符号运算
>> syms q1 q2 f1>> eqx = K*[0 q1 q2].'-[f1 0 0].';
>> [f1,q1,q2]=solve(eqx(1),eqx(2),eqx(3),q1,q2,f1)
f1 =
0
q1 =
-3/2*q2
q2 =
q2
也就是说,f1=0,q2任意取值,q1=-3/2*q2。
求矩阵方程
1、初等变换法:有固定方法,设方程的系数矩阵为A,未知数矩阵为X,常数矩阵为B,即AX=B,要求X,则等式两端同时左乘A^(-1),有X=A^(-1)B。又因为(A,E)~(E,A^(-1)),所以可用初等行变换求A^(-1),从而所有未知数都求出来了。
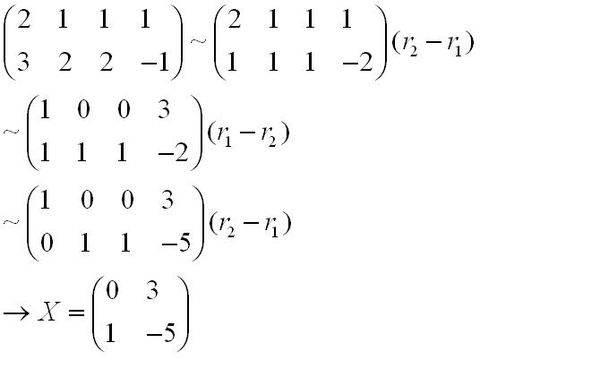
2、逆矩阵求解法:求解方法:容易算出已知矩阵的行列式等于-1。然后计算伴随阵,具体方法是对于编号为mn的元素,划去原阵的第m行和第n列,原阵退化为n-1阶矩阵,求出这个n-1阶阵的行列式,然后填入伴随阵的第n行第m列位置,最后乘以-1的m+n次幂。下面是做法:
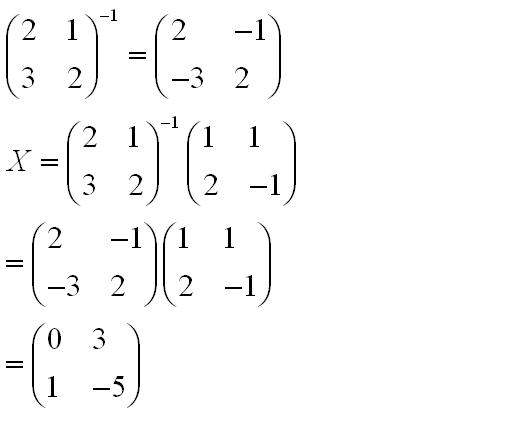
拓展资料:初等变换。
一般采用消元法来解线性方程组,而消元法实际上是反复对方程进行变换,而所做的变换也只是以下三种基本的变换所构成:
(1)用一非零的数乘以某一方程
(2)把一个方程的倍数加到另一个方程
(3)互换两个方程的位置
于是,将变换(1)、(2)、(3)称为线性方程组的初等变换。
参考技术A考察的是矩阵的逆,可以看一下
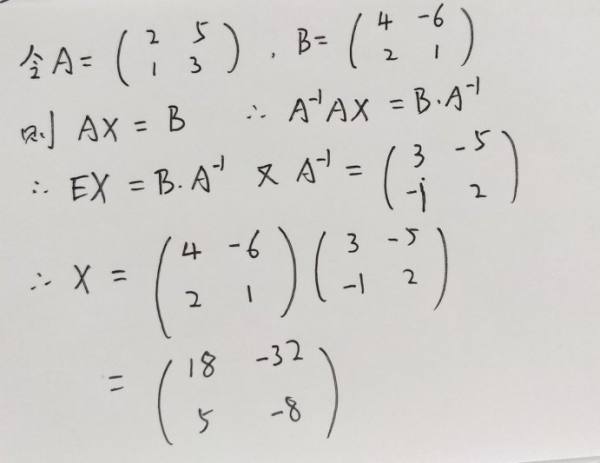
以上是关于matlab 矩阵内含未知数的计算问题的主要内容,如果未能解决你的问题,请参考以下文章