YOLOv5全面解析教程③:更快更好的边界框回归损失
Posted OneFlow深度学习框架
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了YOLOv5全面解析教程③:更快更好的边界框回归损失相关的知识,希望对你有一定的参考价值。

作者|Fengwen、BBuf
边界框回归是目标检测的关键步骤,在现有方法中,虽然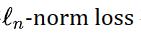 被广泛用于边界框回归,但它不是针对评估指标量身定制的,即 Intersection over Union (IoU)。
被广泛用于边界框回归,但它不是针对评估指标量身定制的,即 Intersection over Union (IoU)。
最近,已经提出了 IoU 损失和 generalized IoU (GIoU) Loss 作为评估 IoU 的指标 ,但仍然存在收敛速度慢和回归不准确的问题。在本文中,我们通过结合预测框和目标框之间的归一化距离来提出距离 -IoU (DIoU) Loss,它在训练中的收敛速度比 IoU 和 GIoU Loss 快得多。
此外,本文总结了边界框回归中的三个几何因素,即重叠面积(overlap area)、中心点距离(central point distance)和高宽比(aspect ratio),在此基础上提出了完全IoU(CIoU)损失,从而促进了更快的收敛和更优的性能。
通过将 DIoU 和 CIoU 损失结合到最先进的目标检测算法中,例如 YOLO v3、SSD 和 Faster RCNN,我们不仅在 IoU 指标方面而且在 GIoU 指标方面都获得了显着的性能提升。此外,DIoU 可以很容易地用于非最大抑制(NMS)作为标准,进一步促进性能提升。(注释:这里IoU指标方面和GIoU指标方面指的是在目标检测精度测量(mAP值 ),IoU损失计算稳定性等一些方面。)
目标检测是计算机视觉任务中的关键问题之一,几十年来一直受到了广泛的研究关注(Redmon et al. 2016; Redmon and Farhadi 2018; Ren et al. 2015; He et al. 2017; Yang et al. 2018; Wang et al. 2019; 2018). 通常,现有的目标检测方法可以分为:
-
单阶段-检测,如YOLO系列 (Redmon et al. 2016; Red- mon and Farhadi 2017; 2018) 和SSD (Liu et al. 2016; Fu et al. 2017),
-
两阶段检测,如 R-CNN系列检测 (Girshick et al. 2014; Girshick 2015; Ren et al. 2015; He et al. 2017),
甚至是多阶段的检测, 像Cascade R-CNN (Cai and Vasconcelos 2018). 尽管存在这些不 同的检测框架,但边界框回归预测一个矩形框来定位目标对象仍然是其中关键步骤。
代码仓库地址:
https://github.com/Oneflow-Inc/one-yolov5
1
前言
本文主要是结合论文Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression(https://arxiv.org/pdf/1911.08287.pdf) 对 IoU 的解析学习。
IoU
IoU介绍
Intersection over Union (IoU)
在指标评估概述的小节有介绍过IoU,已经对IoU有了初步认识(其实在yolov5项目中并不是简单的使用,而是用的后面介绍的CIoU )
计算公式:
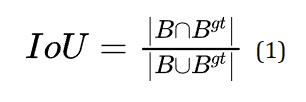
-
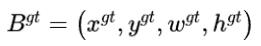 是真实回归框(gt:ground-truth),
是真实回归框(gt:ground-truth), -
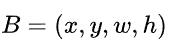 是预测回归框。
是预测回归框。
IoU loss
计算公式:
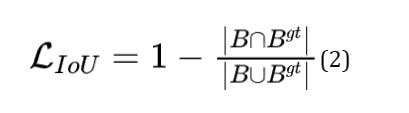
IoU Loss 优缺点分析
有明显的缺陷 IoU loss只在边界框有重叠时才能工作, 对于不重叠的情况不会提供任何移动梯度 (移动代表预测框朝着目标框重叠的方向移动) 。移动梯度表示无法衡量完全不相交的两个框所产生的的损失(iou固定为0),和两个不同形状的预测框可能产生相同的loss(相同的iou)分别如下图的左边和右边所示。
GIoU
GIoU介绍
GIoU的设计初衷就是想解决IoU Loss存在的问题(预测框与真实框不相交时iou恒定为0),设计了一套Generalized Intersection over Union Loss。在IoU的基础上,GIoU还需要找到预测框和真实框的最小外接矩形,然后求出最小外接矩形减去两个预测框union的面积,具体算法流程如下:

GIoU loss
计算公式 :
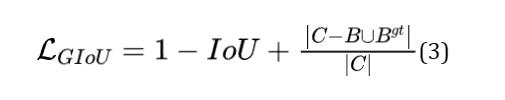
其中C是覆盖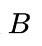 和
和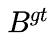 的最小方框,由于引入了C,在不重叠的情况下,预测框也会向目标框移动。
的最小方框,由于引入了C,在不重叠的情况下,预测框也会向目标框移动。
GIoU 优缺点分析
GIoU Loss解决了IoU Loss在不相交情况的问题,在所有性能指标中都可以作为IoU的适当替代品,在目标检测任务中能够得到更高的准确率。
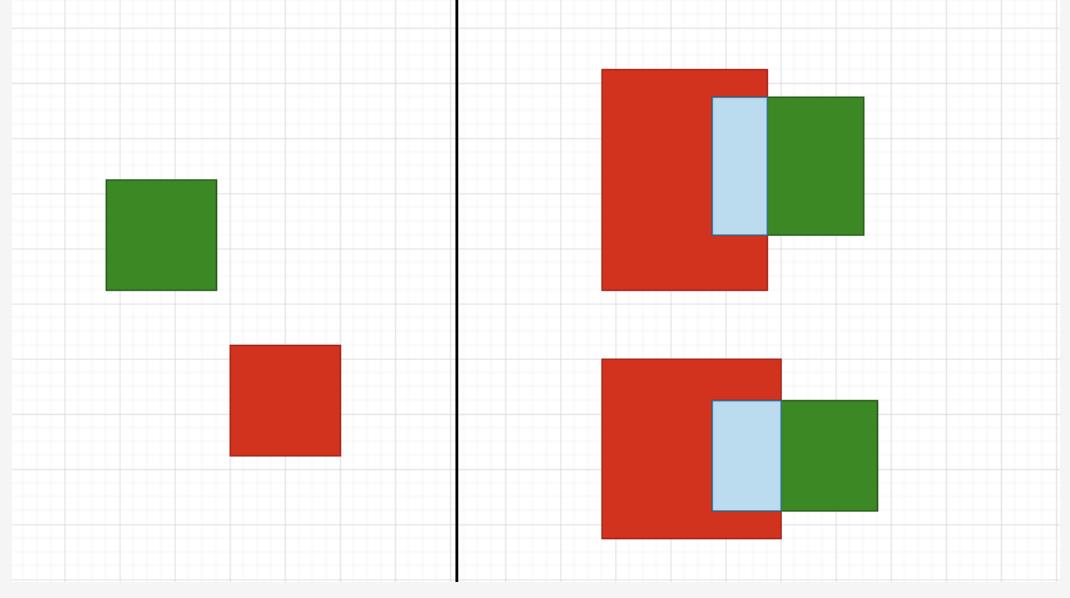
缺点:虽然GIoU可以缓解重叠情况下的梯度消失问题,但它仍有一些局限性。即无法衡量有包含关系时的框回归损失,如下图,三个回归框具有相同的GIoU Loss,但是显然第三个框的回归效果更好。
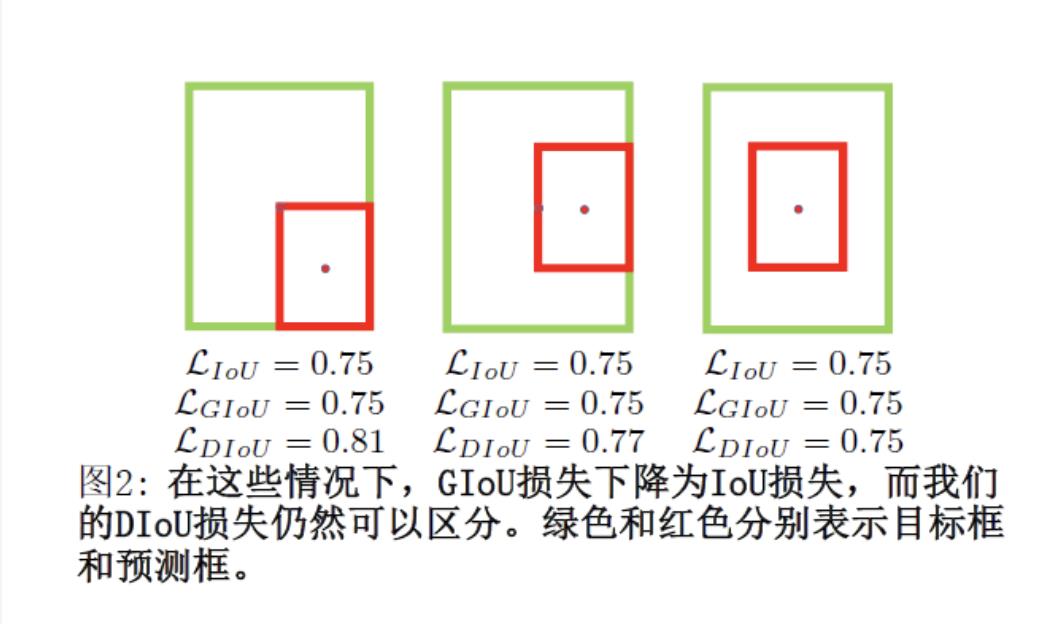
IoU & GIoU 分析
首先,在本文上部分我们分析了关于原始的IoU损失和GIoU 损失的局限性。下面将通过模拟实验结果对边界框回归的过程进行进一步解析。
(补充说明: 为什么要进行模型实验?因为仅仅从检测结果来分析边界框回归的过程很难,因为在不受控制的基准中的回归情况往往不全面比如:不同的距离(distances),不同的尺度(scales)和不同的长宽比(aspect ratios)。相反,进行模拟实验,在实验中综合考虑回归情况,然后就可以很容易地分析给定损失函数的问题。)
模拟实验
在模拟实验中, 我们试图通过距离(distances), 尺度 (scales)和长宽比(aspect ratios)来覆盖边界框之间的大部分关系,如图3(a).所示。特别是, 我们选择7个单位框 (即每个框的面积为 1) ,具有不同的长宽比 (即 1:4、1:3、1:2、1:1、2:1、3:1 和 4:1) 作为目标框。在不失一般性的情况下,7个目标框的中心点被固定在(10,10)。锚框均匀地分散在5000个点上。
1. 距离: 在以半径为 3 的(10,10)为中心的圆形区域内,均匀选择5000个点, 放置7个尺度、7个长宽比的锚框。在这些情况下,重叠和不重叠的方框都被包括。
2. 尺度:对于每个点, 锚框的面积分别设置为0.5、0.67、0.75、1、1.33、1.5 和 2。
3. 长宽比: 对于给定的点和尺度,采用 7 个长宽比,即与目标框遵循相同的设置 (即 1:4、1:3、1:2、1:1、2:1、3:1 和 4:1)。所有 锚箱都对应在每个目标框。综上所述,总共有 个回归案例。
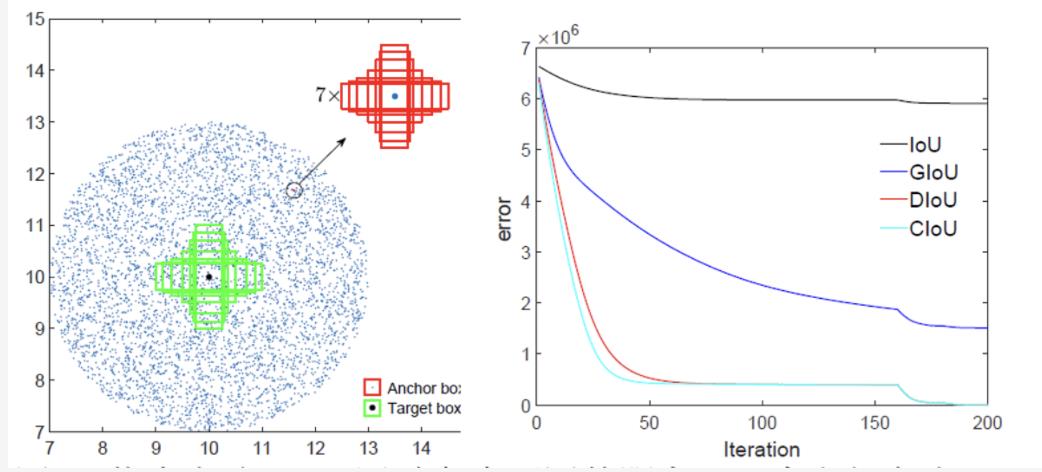
图3: 仿真实验: (a) 通过考虑不同的距离、尺度和长宽比, 采用了171.5万个回归案例。(b)回归误差和(即: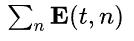 ) 迭代次数为t时不同损失函数的曲线。
) 迭代次数为t时不同损失函数的曲线。
然后通过给定损失函数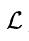 我们可以用梯度下降算法来模拟每种情况下的边界框回归过程
我们可以用梯度下降算法来模拟每种情况下的边界框回归过程 ,对于预测框,当前的预测可以通过:
,对于预测框,当前的预测可以通过:
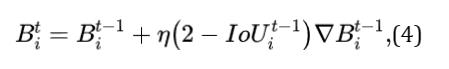
其中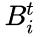 是迭代
是迭代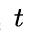 时的预测框,
时的预测框,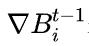 表示损失的梯度。
表示损失的梯度。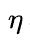 感觉可以理解为学习率。值得注意的是,在我们的实现中,梯度乘
感觉可以理解为学习率。值得注意的是,在我们的实现中,梯度乘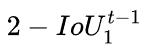 以去加速收敛。边界框回归的性能评估通过使用
以去加速收敛。边界框回归的性能评估通过使用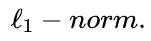 对于每个损失函数, 仿真模拟实验当达到迭代
对于每个损失函数, 仿真模拟实验当达到迭代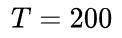 时, 误差曲线如图
时, 误差曲线如图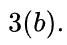 所示。
所示。
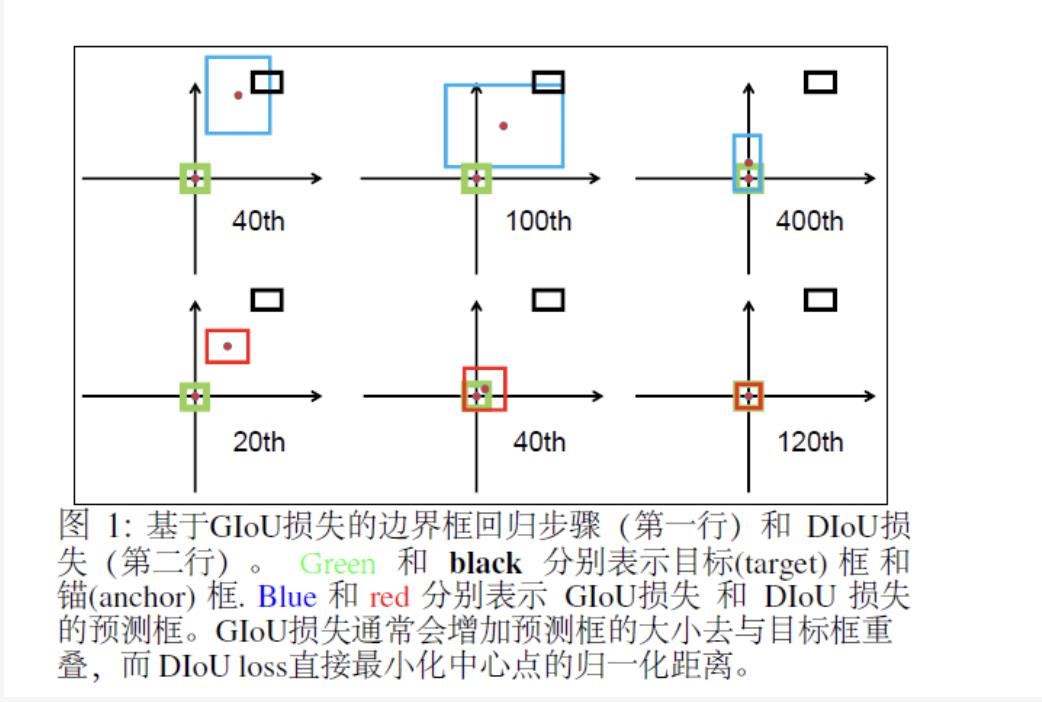
IoU 和 GIoU 损失的限制
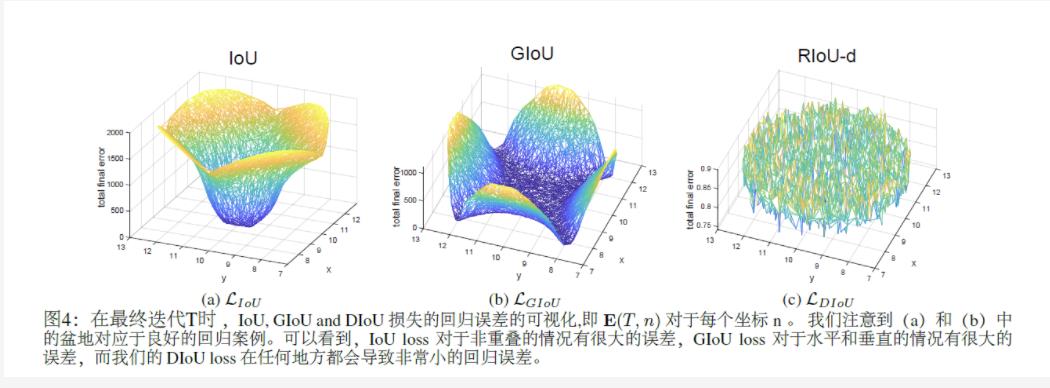
在图4中,我们可视化迭代T时对5000个分散点的最终回归误差。
-
从图4(a)中很容易看出,IoU损失只适用于与目标框重叠的情况。由于∇B总是0,没有重叠的锚框将不会移动。通过添加一个惩罚项见公式(3),
-
GIoU 损失能够更好地缓解非重叠案例的问题,如图所示4(b), 但GIoU的损失显著扩大了盆地,即GIoU的工作面积。但是,在水平方向和垂直方向的情况下,仍然很可能有很大的误差。这是因为GIoU损失中的惩罚项是用来最小化|C−A∪B|,但是C−A∪B的面积通常很小或为0(当两个盒子有包含关系时),然后GIoU几乎退化为IoU损失。只要以适当地学习速率运行足够的迭代GIoU 损失能收敛到很好的解决方案,但收敛速度却是非常慢。从几何上来说,从如图1所示的回归步骤来看,GIoU实际上增大了预测的框大小,用来和目标框重叠,然后IoU项用于预测框与目标框匹配,产生非常缓慢的收敛。
综上所述,在非重叠情况下,IoU损失收敛是糟糕的解决方式,而GIoU损失收敛速度较慢,特别是对于水平和垂直方向的框。在目标检测流程中,IoU和GIoU的损失都不能保证回归的准确性。
DIoU & CIoU
通过前面的IoU和GIoU的分析我们很自然会问以下问题:
-
第一,是否可以直接最小化预测框和目标框之间的归一化距离,以实现更快的收敛?
-
第二,当与目标框有重叠甚至包含时,如何使回归更准确、更快?
DIoU loss
Distance-IoU 损失:更快更好的边界框回归损失,一般来说,IoU-based损失可以定义为:
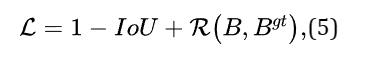
其中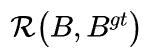 是预测框 B 和目标框
是预测框 B 和目标框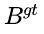 的惩罚项。通过设计适当的惩罚项, 在本节中, 我们提出了 DIoU 损失和 CIoU 损失来解答上述两个问题。
的惩罚项。通过设计适当的惩罚项, 在本节中, 我们提出了 DIoU 损失和 CIoU 损失来解答上述两个问题。
为了回答第一个问题,我们提出将两个边界框的中心点之间的标准化距离最小化,惩罚项可以定义为:
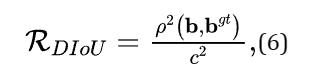
其中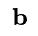 和
和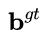 分别代表 B 和
分别代表 B 和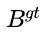 的中心点。
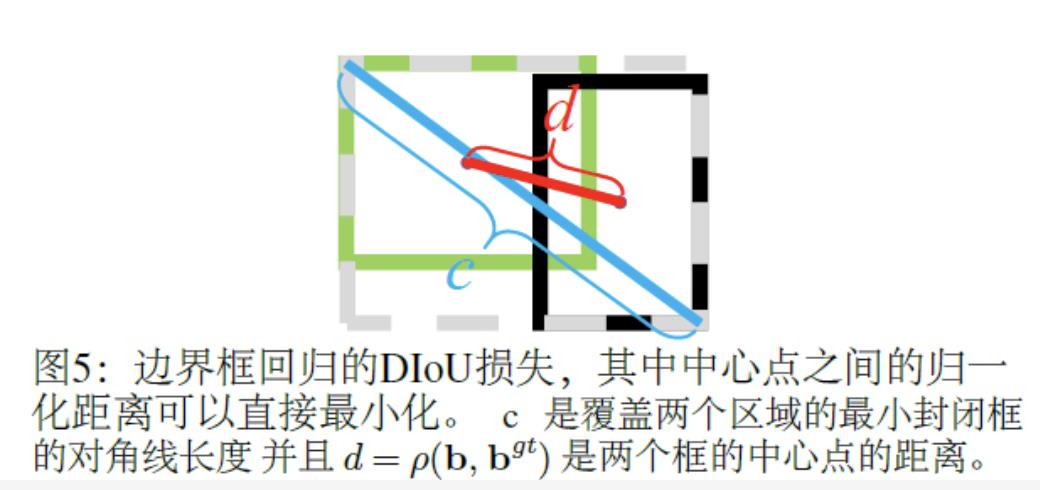
的中心点。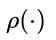 为欧氏距离,C是覆盖两个盒框的最小封闭框的对角线长度。DIoU损失函数可以定义为:
为欧氏距离,C是覆盖两个盒框的最小封闭框的对角线长度。DIoU损失函数可以定义为:
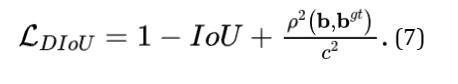
如图5所示,DIoU损失的惩罚项直接使两个中心点之间的距离最小化, 而GIoU损失的目的是减少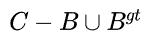 的面积。
的面积。
DIoU 和 IoU/GIoU 损失比较
新提出的DIoU损失继承IoU和GIoU损失的一些属性:
-
DIoU损失对回归问题的尺度仍然是不变的
-
与GIoU损失类似, DIoU损失可以在与目标框不重叠时为边界框提供移动方向。
-
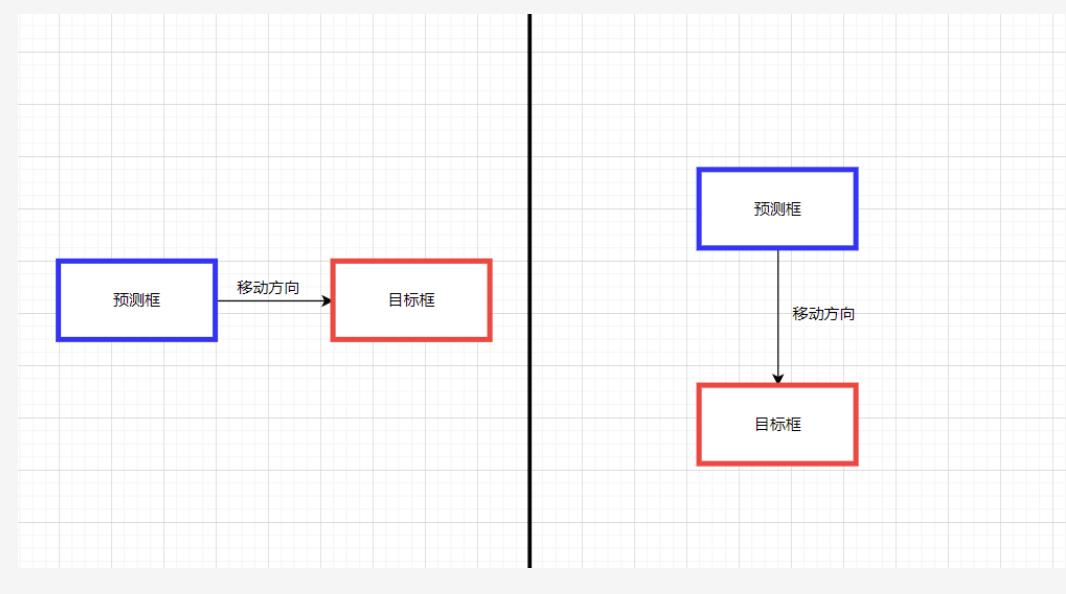
当两个边界框完美匹配时,
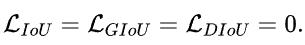 当两个框都很远时,
当两个框都很远时, 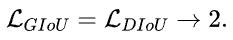
DIoU损失比IoU损失和GIoU损失有几个优点,可以通过仿真实验进行评估。
-
如图1和图3所示,DIoU损失可以直接最小化两个框的距离, 因此收敛速度比GIoU损失要快得多。
-
对于两个框是包含关系的情况(图2),或在水平和垂直方向的情况(图6)下,DIoU损失可以回归非常快,而GIoU损失几乎退化为IoU损失,即
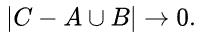
Complete IoU Loss
接着我们回答了第二个问题,提出了边界框回归的良好损失应该要考虑三个重要的几何因素,即重叠面积、中心点距离和长宽比。通过统一坐标IoU损失考虑了重叠区域,而GIoU损失严重依赖于IoU损失。我们提出的DIoU损失旨在同时考虑边界框的重叠面积和中心点距离。然而,边界框的长宽比的一致性也是一个重要的几何因素。因此,基于DIoU损失,通过添加长宽比的一致性来提出CIoU损失:
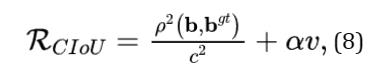
其中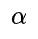 是一个正的权衡参数,
是一个正的权衡参数,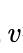 衡量长宽比的一致性。
衡量长宽比的一致性。
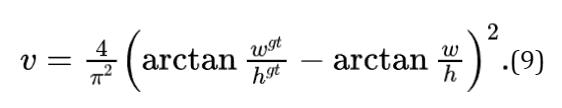
则损失函数可以定义为:
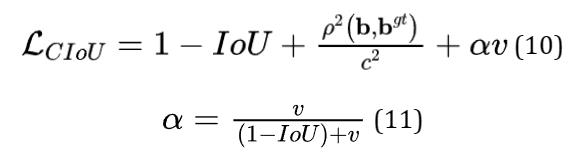
通过重叠面积因子给予更高的优先回归,特别是对于非重叠情况。最终DIoU损失的优化与CIoU损失的优化相同, 除了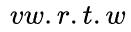 的梯度应该指定W和h。
的梯度应该指定W和h。

主导器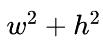 通常是一个很小的值对于
通常是一个很小的值对于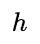 和
和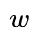 的范围在 [0,1],这很可能会产生梯度爆炸。因此在我们的实现, 主导器
的范围在 [0,1],这很可能会产生梯度爆炸。因此在我们的实现, 主导器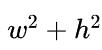 被移除,将步长
被移除,将步长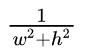 替换为 1,梯度方向仍然与公式(12)一致。
替换为 1,梯度方向仍然与公式(12)一致。
NMS(Non-Maximum Suppression)
2
介绍
NMS是大多数目标检测算法的最后一步,其中删除了冗余的检测框当它与最高分框的重叠超过一个阈值。Soft-NMS (Bodla et al. 2017) 用连续函数w.r.t.惩罚相邻框的检测分数IoU,产生比原始NMS产生更柔和大和更强大的抑制。
IoU-Net (Jiang et al. 2018) 提出了一个新的网络分支来预测定位置信度来指导NMS。最近,自适应NMS(Liu,Huang,和Wang 2019)和 Softer-NMS(He et al. 2019)被提出分别研究适当的阈值策略和加权平均策略。在本工作中,简单将DIoU作为原始NMS的标准,在抑制冗余框时,同时考虑边界框的重叠面积和两个中心点之间的距离。
DioU-NMS
Non-Maximum Suppression using DIoU
在原始的NMS中,IoU指标用于抑制吕余的检测框, 其中重叠区域是唯一的因素, 对于有遮挡的情况,往往会产生错误的抑制。我们在这项工作中建议DIoU是NMS的更好标准,因为在抑制标准中不仅应考虑重叠DIoU-NMS被正式定义为:
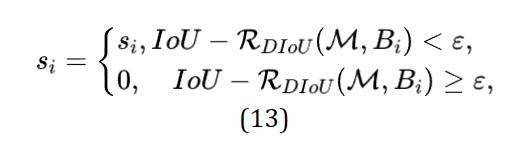
其中框Bi被去除通过同时到考虑IoU和两个框中心点的距离。Si是分类得分和 是NMS阈值。我们认为两个中心点较远的框可能会定位不同的物体,而不应该被删除。此外DIoU-NMS是非常灵活,仅仅是几行的代码就可以集成到任何目标检测管道中。
是NMS阈值。我们认为两个中心点较远的框可能会定位不同的物体,而不应该被删除。此外DIoU-NMS是非常灵活,仅仅是几行的代码就可以集成到任何目标检测管道中。
3
小结
本文主要介绍用于边界框回归的DIoU损失和CIoU损失,以及用于抑制冗余检测框的DIoU-NMS。通过直接最小化两个中心点的归一化的距离,DIoU损失可以比GIoU损失实现更快的收敛。此外CIoU损失考虑了三个几何属性(即重叠区域、中心点距离和长宽比),促进了更快的收敛和更优的性能。
参考文章
-
https://github.com/Zzh-tju/DIoU/blob/master/README.md#introduction
-
https://github.com/Zzh-tju/DIoU/blob/master/README.md#introduction
-
IoU: https://arxiv.org/pdf/1608.01471.pdf
-
GIoU: https://giou.stanford.edu/GIoU.pdf
-
DIoU: https://arxiv.org/pdf/1911.08287.pdf
其他人都在看
欢迎Star、试用OneFlow最新版本:
以上是关于YOLOv5全面解析教程③:更快更好的边界框回归损失的主要内容,如果未能解决你的问题,请参考以下文章