用Matlab实现黄金分割法，优化目标函数minf(x)=2x^2-x-1，初始区间为[-1,1],e=0.001

Posted 2023-05-07

求高手帮忙！急！急！急！

首先在matlab新建文件保存为goldmin.m

function[x,y] = goldmin(f,xa,xb,s)

% 黄金分割法求解函数最小值

% 输入

% f 待优化函数

g = (sqrt(5)-1)/2; % 黄金分割比，0.618

a = xa;

b = xb;

x2 = a + g*(b-a);

x1 = a + b - x2;

y1 = f(x1);

y2 = f(x2);

while abs(b-a) > s

if y1<y2

b = x2;

x2 = x1;

x1 = a + b - x2;

end

>> f = @(x) 2*x^2-x-1;

>> [x,y]=goldmin(f,-1,1,0.001)

x =

0.2497

y =

-1.1250

>>

即当x=0.2497时取最小值-1.125

菲波那契数列

经研究发现，相邻两个菲波那契数的比值是随序号的增加而逐渐趋于黄金分割比的。即f(n-1)/f(n)→0.618…。由于菲波那契数都是整数，两个整数相除之商是有理数，所以只是逐渐逼近黄金分割比这个无理数。但是当我们继续计算出后面更大的菲波那契数时，就会发现相邻两数之比确实是非常接近黄金分割比的。

参考技术A

窗口命令

gold_mean(-1,1,0.001)

ans =

.2499143985

代码见附件

文件1，gold_fun.m    目标函数

文件2，gold_mean.m   黄金分割法函数

参考技术B 首先在matlab新建文件保存为goldmin.m
function[x,y] = goldmin(f,xa,xb,s)
% 黄金分割法求解函数最小值
% 输入
% f 待优化函数
% a,b 区间
% s 精度
% 输出
% x 最优解
% y 最优解对应的最小值
%%
g = (sqrt(5)-1)/2; % 黄金分割比，0.618
a = xa;
b = xb;
x2 = a + g*(b-a);
x1 = a + b - x2;
y1 = f(x1);
y2 = f(x2);
while abs(b-a) > s
if y1<y2
b = x2;
x2 = x1;
x1 = a + b - x2;
end
if y1>=y2
a = x1;
x1 = x2;
x2 = a + b - x1;
end
y1=f(x1);
y2 = f(x2);
end
x = x1;
y = f(x);
然后在命令区输入
>> f = @(x) 2*x^2-x-1;
>> [x,y]=goldmin(f,-1,1,0.001)

x =

0.2497

y =

-1.1250

>>
即当x=0.2497时取最小值-1.125本回答被提问者和网友采纳

第九章 罚函数法

内容来自马昌凤编著的《最优化方法及其Matlab程序设计》，文章仅为个人的学习笔记，感兴趣的朋友详见原书。

罚函数法的基本思想：根据约束条件的特点，将其转化为某种惩罚函数加到目标函数中去，从而将约束优化问题转化为一系列的无约束优化问题来求解。

1.外罚函数法

算法

示例

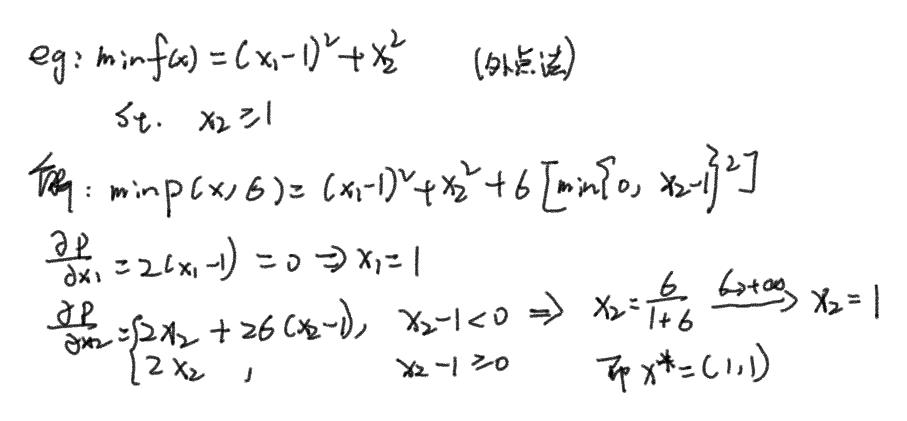
2.内点法

内点法仅适用于不等式约束的优化问题
$minf(x),x\in R^n$
$s.t.g_i(x)\ge 0,i=1,...,m$

基本思想：保持每一个迭代点$x_k$都是可行域$D$的内点，可行域的边界被筑起一道很高的“围墙”作为障碍，当迭代点靠近边界时，增广目标函数值骤然增大，以示“惩罚”，并阻止迭代点穿越边界。

算法

示例

故对一般约束问题的内点法，等式约束利用“外罚函数”的思想，而不等式约束则利用“障碍函数”的思想构造出混合增广目标函数。

3.乘子法

基本思想：从原问题的拉格朗日函数出发，再加上适当的罚函数，从而将原问题转化为求解一系列的无约束优化子问题

等式约束问题的乘子法

不等式约束问题的乘子法

为等式约束的推广，即先引进辅助变量把不等式约束化为等式约束，再利用最优性条件消去辅助变量。

程序

增广拉格朗日函数

function psi=mpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma)
f=feval(fun,x);  he=feval(hf,x);  gi=feval(gf,x);
l=length(he); m=length(gi);
psi=f;  s1=0.0;
for(i=1:l)
    psi=psi-he(i)*mu(i);
    s1=s1+he(i)^2;
end
psi=psi+0.5*sigma*s1;
s2=0.0;
for(i=1:m)
    s3=max(0.0, lambda(i) - sigma*gi(i));
    s2=s2+s3^2-lambda(i)^2;
end
psi=psi+s2/(2.0*sigma);

增广拉格朗日函数的梯度

function dpsi=dmpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma)
dpsi=feval(dfun,x);
he=feval(hf,x);  gi=feval(gf,x);
dhe=feval(dhf,x);  dgi=feval(dgf,x);
l=length(he); m=length(gi);
for(i=1:l)
    dpsi=dpsi+(sigma*he(i)-mu(i))*dhe(:,i);
end
for(i=1:m)
    dpsi=dpsi+(sigma*gi(i)-lambda(i))*dgi(:,i);
end

乘子法程序

function [x,mu,lambda,output]=multphr(fun,hf,gf,dfun,dhf,dgf,x0)
% 功能: 用乘子法解一般约束问题:  min f(x), s.t. h(x)=0, g(x)>=0
%输入:  x0是初始点, fun, dfun分别是目标函数及其梯度；
%   hf, dhf分别是等式约束（向量）函数及其Jacobi矩阵的转置；
%   gf, dgf分别是不等式约束（向量）函数及其Jacobi矩阵的转置；
%输出:  x是近似最优点，mu, lambda分别是相应于等式约束和不
%   等式约束的乘子向量；output是结构变量，输出近似极小值f, 迭
%   代次数
maxk=500;   %最大迭代次数
sigma=2.0;  %罚因子
eta=2.0;  theta=0.8;  %PHR算法中的实参数
k=0; ink=0;  %k, ink分别是外迭代和内迭代次数
epsilon=1e-5;  %终止误差值
x=x0;  he=feval(hf,x); gi=feval(gf,x);
n=length(x); l=length(he); m=length(gi);
%选取乘子向量的初始值
mu=0.1*ones(l,1);  lambda=0.1*ones(m,1);
btak=10;  btaold=10;  %用来检验终止条件的两个值
while(btak>epsilon & k<maxk)
    %调用BFGS算法程序求解无约束子问题
    [x,ival,ik]=bfgs('mpsi','dmpsi',x0,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma);
    ink=ink+ik; 
    he=feval(hf,x); gi=feval(gf,x);
    btak=0.0;
    for (i=1:l), btak=btak+he(i)^2;   end
    for i=1:m
        temp=min(gi(i),lambda(i)/sigma);
        btak=btak+temp^2;
    end
    btak=sqrt(btak);   
    if btak>epsilon
        if(k>=2 & btak > theta*btaold)
            sigma=eta*sigma;
        end
        %更新乘子向量
        for (i=1:l),  mu(i)=mu(i)-sigma*he(i);  end
        for (i=1:m)
            lambda(i)=max(0.0,lambda(i)-sigma*gi(i));
        end
    end
    k=k+1;
    btaold=btak;
    x0=x;
end
f=feval(fun,x);
output.fval=f;
output.iter=k;
output.inner_iter=ink;
output.bta=btak;
%xstar=[0.5*(sqrt(7)-1);0.25*(sqrt(7)+1)];
%err1=norm(x-xstar)