游戏开发答疑马里奥派对选面积大作战玩法的功能实现（Unity | 算法 | 四邻域 | 连通块 | 面积比例分割）

Posted 2023-02-05 林新发

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了游戏开发答疑马里奥派对选面积大作战玩法的功能实现（Unity | 算法 | 四邻域 | 连通块 | 面积比例分割）相关的知识，希望对你有一定的参考价值。

本文运行效果如下

文章目录

一、前言

嗨，大家好，我是新发。
有同学私信问了我一个问题，如下

游戏视频如下

【超级马力欧派对】（四十六）选面积大作战

我以第一回合为例，也就是把5*9的方格分成9:11:12:13的面积，并且确保面积是四邻域连通的，什么是四邻域呢？一个格子的上下左右紧邻的格子就是它的四邻域。

好了，下面讲一下实现方案。

二、实现方案

1、构造二维数组

为了演示，我先做了一个简单的UI界面，如下，下面是一个5*9的方格阵列，

如果对应成代码，它就是一个二维数组，像这样子

/// <summary>
/// 行数
/// </summary>
private const int ROW_CNT = 5;
/// <summary>
/// 列数
/// </summary>
private const int COL_CNT = 9;

/// <summary>
/// 格子二维数组
/// </summary>
public Image[,] grid = new Image[ROW_CNT, COL_CNT];

2、顺序填充颜色

我们定义四种颜色，

把格子按9:11:12:13的比例顺序填充不同的颜色，像这样子

对应成代码就是这样子：

// 划分成4种颜色，9个color1, 11个color2, 12个color3, 13个color4
for (int i = 0; i < ROW_CNT; ++i)
  
      for (int j = 0; j < COL_CNT; ++j)
      
          var index = i * COL_CNT + j;
          if (index < 9)
          
              grid[i, j].color = color1;
          
          else if (index < 9 + 11)
          
              grid[i, j].color = color2;
          
          else if (index < 9 + 11 + 12)
          
              grid[i, j].color = color3;
          
          else
          
              grid[i, j].color = color4;

3、交换格子颜色

对某两个格子进行交换，写成代码是这样子，

int i1 = Random.Range(0, ROW_CNT);
int j1 = Random.Range(0, COL_CNT);

int i2 = Random.Range(0, ROW_CNT);
int j2 = Random.Range(0, COL_CNT);

var tmpColor = grid[i1, j1].color;
grid[i1, j1].color = grid[i2, j2].color;
grid[i2, j2].color = tmpColor;

交换后有两种结果：
情况1： 没有破坏连通性，依然是4个大的连通块：

情况2： 破坏了原有的连通性，像这样子，出现了7个连通块：

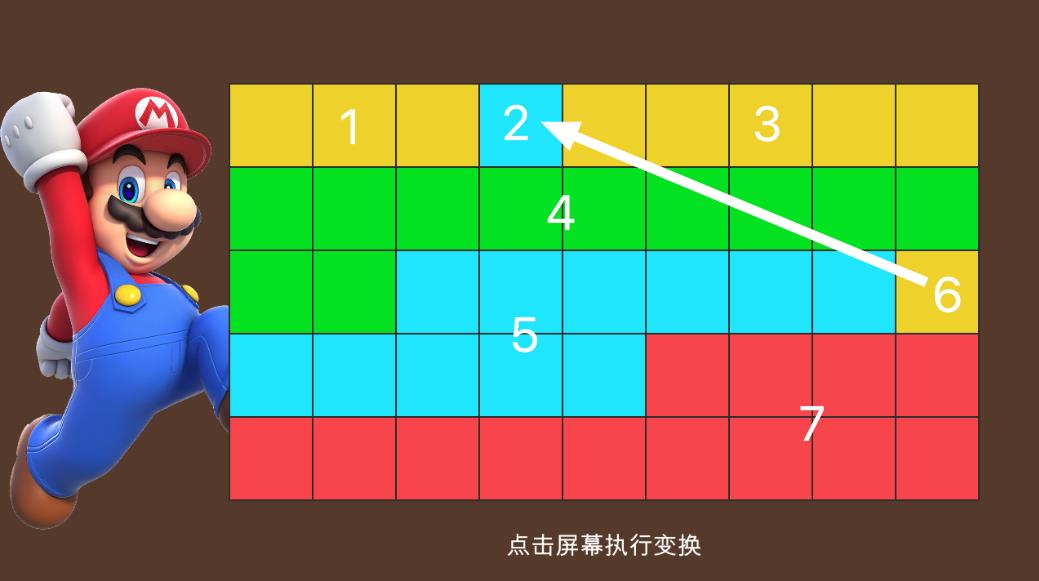
如果破坏了原来的连通性，这次交换就要作废。

那，我们如何检测有没有破坏原来的连通性呢？这个问题等效于：我们如何检查连通块的个数呢？只要确保连通块的个数是4，就说明没有破坏原来的连通性。

4、计算连通块个数（四邻域连通）

这里我用的是深度优先遍历，通过递归来实现。

首先我们定义格子的状态值：0或1，如果被遍历过，则标记为1；我们可以定义一个二维数组来存储格子状态：

/// <summary>
/// 格子状态，遍历过的标记为为1，否则为0
/// </summary>
int[,] ergodic = new int[ROW_CNT, COL_CNT];

为了存储四邻域连通的个数，我们再定义一个变量

/// <summary>
/// 统计连通块个数
/// </summary>
int connectGroupCnt = 0;

然后从[0, 0]的位置开始，如果发现格子状态为0，则让connectGroupCnt自增1，把格子标记为1，然后遍历格子的上下左右邻域的格子，如果发现颜色与当前格子相同，则标记为1，否则不操作，以此类推，直到全部遍历完毕。
为了方便大家对这个过程有个更直观的感受，我特意做了个动态图，如下

对应成代码如下

/// <summary>
/// 检测连通性
/// </summary>
/// <returns></returns>
bool CheckContinuous()

    int i = 0;
    connectGroupCnt = 0;
    ergodic = new int[ROW_CNT, COL_CNT];

    while (i < ROW_CNT)
    
        int j = 0;
        while (j < COL_CNT)
        
            Dfs(i, j, grid);
            j++;
        
        i++;
    

    // 如果四连通块超过4个，则说明产生了不连续颜色块
    if (connectGroupCnt > 4)
        return false;

    return true;



/// <summary>
/// 深度优先，递归调用，计算连通块数量
/// </summary>
void Dfs(int x, int y, Image[,] grid)

    if (x < 0 || y < 0 || x == ROW_CNT || y == COL_CNT)
    
        return;
    
    if (ergodic[x, y] == 0)
    
        ergodic[x, y] = 1;
        connectGroupCnt++;

    
    // 右
    if (y < COL_CNT - 1 && grid[x, y].color == grid[x, y + 1].color && ergodic[x, y + 1] == 0)
    
        ergodic[x, y + 1] = 1;
        Dfs(x, y + 1, grid);
    
    // 左
    if (y > 0 && grid[x, y].color == grid[x, y - 1].color && ergodic[x, y - 1] == 0)
    
        ergodic[x, y - 1] = 1;
        Dfs(x, y - 1, grid);
    
    // 下
    if (x < ROW_CNT - 1 && grid[x, y].color == grid[x + 1, y].color && ergodic[x + 1, y] == 0)
    
        ergodic[x + 1, y] = 1;
        Dfs(x + 1, y, grid);
    
    // 上
    if (x > 0 && grid[x, y].color == grid[x - 1, y].color && ergodic[x - 1, y] == 0)
    
        ergodic[x - 1, y] = 1;
        Dfs(x - 1, y, grid);