OpenGL学习脚印: 视变换(view transformation)

Posted 2023-02-04 The fool

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了OpenGL学习脚印: 视变换(view transformation)相关的知识，希望对你有一定的参考价值。

写在前面
OpenGL中的坐标处理过程包括模型变换、视变换、投影变换、视口变换等内容，这个主题的内容有些多，因此分节学习，主题将分为5节内容来学习。上一节模型变换，本节学习模型变换的下一阶段——视变换。到目前位置，主要在2D下编写程序，学习了视变换后，我们可以看到3D应用的效果了。本节示例程序均可在我的github下载。

通过本节可以了解到

视变换的概念
索引绘制立方体
LookAt矩阵的推导(对数学不感兴趣，可以跳过)
相机位置随时间改变的应用程序

坐标处理的全局过程(了解，另文详述)

OpenGL中的坐标处理包括模型变换、视变换、投影变换、视口变换等内容，具体过程如下图1所示:

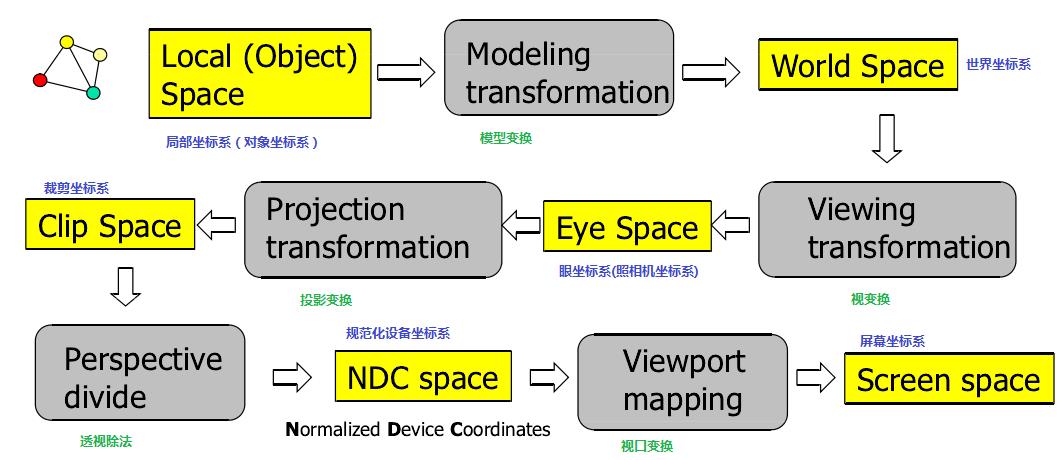
每一个过程处理都有其原因，这些内容计划将会在不同节里分别介绍，最后再整体把握一遍。
今天我们学习第二个阶段——视变换。

并不存在真正的相机

OpenGL成像采用的是虚拟相机模型。在场景中你通过模型变换，将物体放在场景中不同位置后，最终哪些部分需要成像，显示在屏幕上，主要由视变换和后面要介绍的投影变换、视口变换等决定。

其中视变换阶段，通过假想的相机来处理矩阵计算能够方便处理。对于OpenGL来说并不存在真正的相机，所谓的相机坐标空间(camera space 或者eye space)只是为了方便处理，而引入的坐标空间。

在现实生活中，我们通过移动相机来拍照，而在OpenGL中我们通过以相反方式调整物体，让物体以适当方式呈现出来。例如，初始时，相机镜头指向-z轴，要观察-z轴上的一个立方体的右侧面，那么有两种方式：

相机绕着+y轴，旋转+90度，此时相机镜头朝向立方体的右侧面，实现目的。注意这时立方体并没有转动。
相机不动，让立方体绕着+y轴，旋转-90度，此时也能实现同样的目的。注意这时相机没有转动。完成这一旋转的矩阵记作 $R_y(-\\frac\\pi2)$

在OpenGL中，采用方式2来完成物体成像的调整。例如下面的图表示了假想的相机：

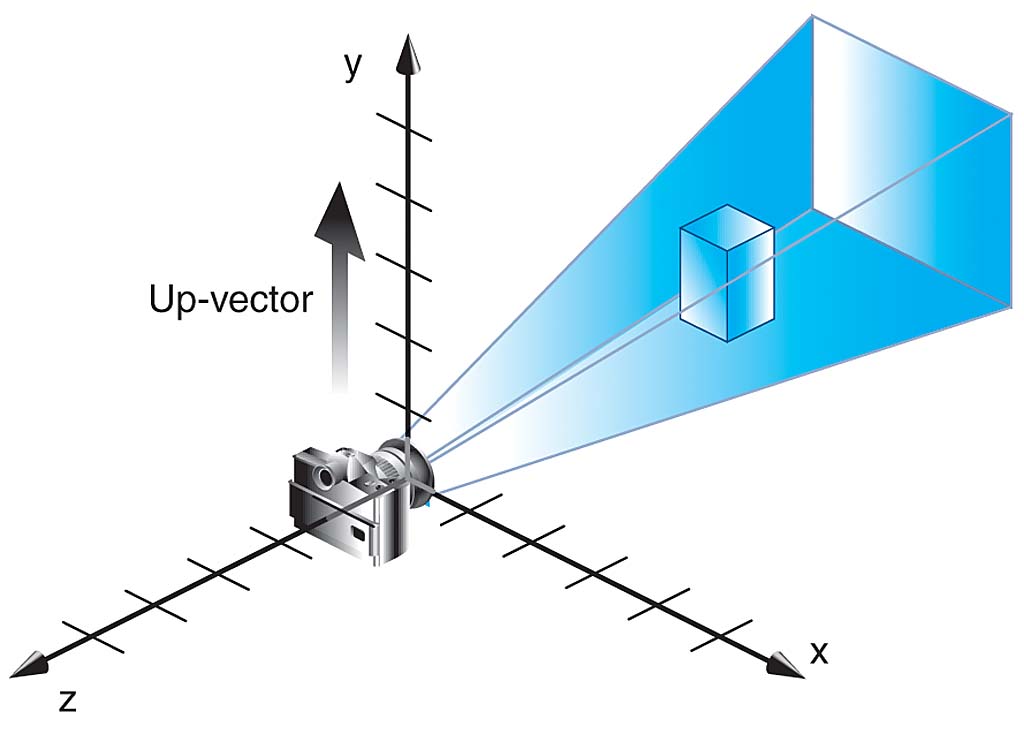
进一步说明

进一步说明这里相对的概念，对这个概念不感兴趣的可以跳过。默认时相机位于(0,0,0)，指向-z轴，相当于调用了：

glm::lookAt(glm::vec(0.0f,0.0f,0.0f),
        glm::vec3(0.0f, 0.0f, -1.0f),
        glm::vec3(0.0f, 1.0f, 0.0f)),

得到是单位矩阵，这是相机的默认情况。

上述第一种方式，相机绕着+y轴旋转90度，相机指向-x轴，则等价于调用变为:

   glm::mat4 view =glm::lookAt(glm::vec(0.0f,0.0f,0.0f),
        glm::vec3(-1.0f, 0.0f, 0.0f),
        glm::vec3(0.0f, 1.0f, 0.0f)),

得到的视变换矩阵为:

view=⎡⎣⎢⎢⎢00100100−10000001⎤⎦⎥⎥⎥ $view =\\beginbmatrix 0 & 0 & -1 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 1 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 1 \\endbmatrix$

上述第二种方式，通过立方体绕着+y轴旋转-90度，则得到的矩阵M,相当于:

   glm::mat4 model = glm::rotate(glm::mat4(1.0), glm::radians(-90.0f), glm::vec3(0.0, 1.0, 0.0));

这里得到的矩阵M和上面的矩阵view是相同的，可以自行验证下。
也就是说，通过旋转相机+y轴90度，和旋转立方体+y轴-90度，最终计算得到的矩阵相同。调整相机来得到观察效果，可以通过相应的方式来调整物体达到相同的效果。在OpenGL中并不存在真正的相机，这只是一个虚构的概念。

视变换矩阵的推导（了解，对数学不感兴趣可跳过）

相机坐标系由相机位置eye和UVN基向量(或者说由forward, side ,up）构成，如下图所示：

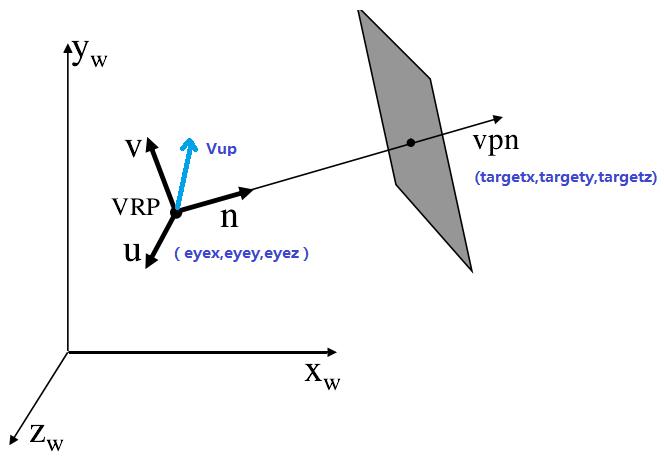
各个参数的含义如下：

相机位置也称为观察参考点 (View Reference Point) 在世界坐标系下指定相机的位置eye。
相机镜头方向，由相机位置和相机指向的目标(target)位置计算出， $forwrad=(target - eye)$ 。
相机顶部正朝向: View Up Vector 确定在相机哪个方向是向上的，一般取(0, 1, 0)。这个参数稍后详细解释。

上面的图简化为：

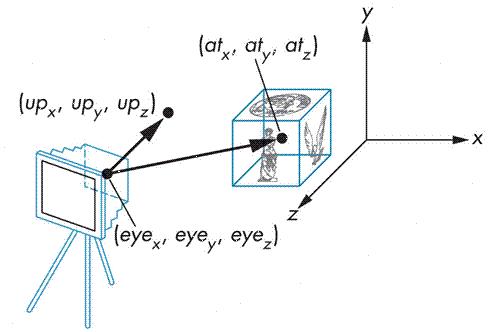
在使用过程中，我们是要指定的参数即为相机位置(eye)，相机指向的目标位置(target)和viewUp vector三个参数。
Step1 : 首选计算相机镜头方向 $forwrad=(target - eye)$ ,
进行标准化 $forward = \\fracforward\\| forwrad\\|$ 。
Step2: 根据view-up vector和forward确定相机的side向量:
$viewUp\' = \\fracviewUp\\| viewUp\\|$
$side = cross(forward, viewUp\')$

Step3 : 根据forward和side计算up向量:
$up = cross(side, forward)$
这样eye位置，以及forward、side、up三个基向量构成一个新的坐标系，注意这个坐标系是一个左手坐标系，因此在实际使用中，需要对forward进行一个翻转，利用-forward、side、up和eye来构成一个右手坐标系。

我们的目标是计算世界坐标系中的物体在相机坐标系下的坐标，也就是从相机的角度来解释物体的坐标。从一个坐标系的坐标变换到另一个坐标系，这就是不同坐标系间坐标转换的过程。

计算方法1——直接计算变换矩阵

从坐标和变换一节，了解到，要实现不同坐标系之间的坐标转换，需要求取一个变换矩阵。而这个矩阵就是一个坐标系A中的原点和基在另一个坐标系B下的表示。
我们将相机坐标系的原点和基，使用世界坐标系表示为(s代表side基向量，u代表up基向量，f代表forward基向量)：

[Camera]world=⎡⎣⎢⎢⎢⎢s[0]s[1]s[1]0u[0]u[1]u[2]0−f[0]−f[1]−f[2]0eyexeyeyeyez1⎤⎦⎥OpenGL学习脚印: 视变换(view transformation)

OpenGL学习脚印: 坐标变换过程(vertex transformation)

OpenGl从零开始之坐标变换

翻译我的OpenGL学习进阶之旅世界（World）视图（View）和投影变换矩阵（Projection Transformation Matrices）

OpenGL学习脚印: 绘制一个三角形