阿波罗，赫利俄斯，赫里厄斯是啥关系？

Posted 2023-05-05

参考技术A 阿波罗[Apollo]希腊神话中最重要的神祗之一，宙斯和女神勒托之子，阿尔忒弥斯的孪生兄弟，俄耳甫斯、利诺斯、阿斯克勒皮俄斯（或叫埃斯库拉皮俄斯）之父。勒托怀了阿波罗和阿尔忒弥斯后，心怀嫉妒的赫拉不许她在陆地上分娩。于是根据宙斯的旨意，在海里出现了得洛斯岛，勒托在这里生下了双胞胎阿波罗和阿尔忒弥斯。关于阿波罗的神话流传：
1、阿波罗在得尔菲地方杀死了为害的凶龙皮托，于是在当地修建了得尔菲神庙。阿波罗也得了一个别名：阿波罗——皮托。
2、阿波罗同奥林波斯的神祗一起，参加了反对巨人的斗争。
3、阿波罗同阿尔忒弥斯一起杀死侮辱了勒托的巨人提梯俄斯。
4、阿波罗同阿尔忒弥斯一起杀死了侮辱勒托的尼俄柏的孩子们。
5、在特洛亚战争中，由于希腊人侮辱了阿波罗的祭司克律塞斯，阿波罗给希腊军队降下了瘟疫。
6、赫尔墨斯把他发明的竖琴给了阿波罗，因此阿波罗成了成了音乐之神，诗神之首。
7、马耳叙阿斯由于胆敢同阿波罗较量音乐艺术而被阿波罗剥了皮。
8、特洛亚的公主卡珊德拉曾许诺，如果阿波罗赋予她先知的才能，她就嫁给阿波罗。阿波罗这样做了，但卡珊德拉却没有履行诺言。于是，阿波罗使人们都不相信她的预言。
9、阿波罗爱上了自然女神达佛涅，达佛涅为了逃避阿波罗的追逐，变成了月桂树，于是月桂树就成了阿波罗的圣树。
10、阿波罗之子阿斯克勒皮俄斯擅长医术，甚至能死起回生，宙斯认为他破坏了神规，就用认电把他击死。为了给儿子复仇，阿波罗把给宙斯制造闪电的库克洛佩斯全部杀死。为此，宙斯罚阿波罗给阿德墨托斯服苦役七年。
11、阿波罗同波塞冬一起为特洛亚王拉俄墨冬效力，并为特洛亚城筑起了牢不可破的城墙。
12、阿波罗答应枯迈的西彼拉可以请求任何一件事情。西彼拉请求她的生命能象她拿的沙粒一样长久，但却忘记请求永葆青春。之后她变得老朽不堪，便把自己吊在一只桶里。人们问她希望什么，她说她只希望死。
13、阿波罗同库瑞涅相爱，库瑞涅是河神佩纽斯之曾孙女，勇敢、敏捷，在佩利翁山上赤手斗雄狮，因而被阿波罗看中。阿波罗把她带到非洲一地，以后此处便以库瑞涅命名，他们生子阿里斯泰俄斯。
关于阿波罗的神话来源，有两种不同的理论。一种认为，阿波罗的传说最初可能流传在希腊的北方。因为北方对于阿波罗的信仰甚为普遍而且悠久。传说中的许佩耳波里亚人是阿波罗的人民，他们也生活在北方。传说他们每年向得洛斯献纳祭品。在得尔菲的斯忒普忒里亚大祭也是面向北方的。
另一种理论认为，对阿波罗的崇拜可能来自小亚细亚。以下事实可以证明：
1、在特洛亚的战争中，阿波罗站在特洛亚人一方。
2、阿波罗的一些最重要的神庙都在小亚细亚。
3、有些学者认为：“阿波罗”一词源自小亚细亚语，其意义为“门”，并认为，最初阿波罗可能是守护家庭或城市的门神。阿波罗的别名之一叫“看门的”。
对阿波罗的崇拜大约在迈锡尼时代（公元前2000年）传入希腊。阿波罗的许多别名证明关于他的神话极为古老，也证明了阿波罗最初来源于图腾。他的别名有“狼”、“鼠”等，这大约就是阿波罗的最初形象。阿波罗被视为保护人、畜和庄稼不受狼、鼠危害的神。
在雅典以及其他希腊城市里，阿波罗又被奉为路神和航海神。
在相当早的时候，阿波罗已经是太阳神，因此在诗歌中阿波罗又有另一个名字“福玻斯”，意即为“光亮的”。也许这个名字是在奥林波斯神系排挤了地方神福玻斯之后产生的。
随着希腊宗教的发展，阿波罗同赫利俄斯合在一起。阿波罗作为太阳神还保护农业。在阿提卡，夏天和秋天都有祭祀他的节日。然而阿波罗作为农业神却不如作为战神重要。阿波罗的神光——太阳光——被看作金箭，可以自远处伤人。古代人认为人的遽死就是由于被阿波罗的神箭射中。由于战争多是贵族们的事情，阿波罗在贵族中间尤为有名。
信奉阿波罗的中心地区是得洛斯岛，这里每四年举行一次竞技大会，希腊各城邦都有代表参加。通过希腊在意大利的殖名地，信奉阿波罗也传入罗马。
公元前31年，在罗马修建了阿波罗神庙。奥古斯都大帝宣布阿波罗为他的保护神，并规定为阿波罗举行竞技大会。向阿波罗祭献的贡品是月桂和棕榈。阿波罗的神物是狼、海豚、鹰、鼠、蜥蜴等。在最古老的造型艺术中，阿波罗是高大、端正、长发、无须的青年。他的表征物是竖琴、弓、神盾。
在希腊化时期，阿波罗被刻画为弹着竖琴，坐势的裸体青年。斯科帕斯、勒俄卡瑞斯、普剌克西忒勒斯等雕刻的阿波罗像，只有复制品流传下来。

赫利俄斯[Helios]太阳神，提坦许佩里翁和忒亚之子，月亮女神塞勒涅和黎明女神厄俄斯的兄弟，法厄同和赫利阿得斯之父。
在荷马的笔下，除了掌管天（宙斯）、地（哈得斯）和水（波塞冬）这三大神以外，还有一位洞察一切位居第四的大神赫利俄斯。
在古典时代赫利俄斯是太阳光神，他可以使盲人复明，也可以使明眼人变瞎。
自公元前5世纪起，赫利俄斯同阿波罗合在了一起。根据神话，赫利俄斯每天早晨从东方起来，乘上由四匹口中喷火的神马牵引的太阳车，穿过天空，到晚上就落入西方的海洋，然后乘小舟在一夜之间返回东方。
在西西里的特里那克亚岛，赫利俄斯的女儿费图萨和兰佩提亚饲养着他的牛、羊群。
据传说，赫利俄斯的马群在布勒塞德岛饲养，那里生长着一种专门饲养神马的草。
在科任托斯、阿耳戈斯、厄利斯等地都有赫利俄斯的神庙，但崇奉赫利俄斯的主要地方是罗得斯岛。
赫利俄斯在罗马神话中叫索尔。他的祭物有公羊、公牛、羔羊、蜂蜜、白马和熊等。在造型艺术中，赫利俄斯乘着车，头顶上光芒四射。 参考技术B 是同一个人

求f(x)=xsinx的傅里叶级数

设f（x）=sinax，-π≤x≤π，a>0，将其展开成以2π为周期的傅里叶级数。

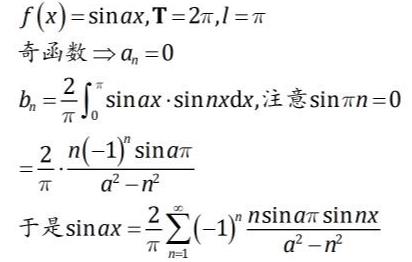
设f(t)为一非正弦周期函数，其周期为T，频率和角频率分别为f , ω1。由于工程实际中的非正弦周期函数，一般都满足狄里赫利条件，所以可将它展开成傅里叶级数。

收敛性

傅里叶级数的收敛性：满足狄利赫里条件的周期函数表示成的傅里叶级数都收敛。狄利赫里条件如下：

在任何周期内，x(t)须绝对可积；在任一有限区间中，x(t)只能取有限个最大值或最小值；

在任何有限区间上，x(t)只能有有限个第一类间断点。

吉布斯现象：在x(t)的不可导点上，如果我们只取（1）式右边的无穷级数中的有限项作和x(t)，那么x(t)在这些点上会有起伏。一个简单的例子是方波信号。

以上内容参考：百度百科-傅里叶级数

参考技术A 一个是简写，一个是具体囊括写出！
就比如说(2x+3)的平方，这个是简写；让你写出它的展开式
但傅里叶级数一般都是无穷的，都用n表示 参考技术B 一． 傅里叶级数的三角函数形式
　　设f(t)为一非正弦周期函数，其周期为T，频率和角频率分别为f , ω1。由于工程实际中的非正弦周期函数，一般都满足狄里赫利条件，所以可将它展开成傅里叶级数。即
　　其中A0/2称为直流分量或恒定分量；其余所有的项是具有不同振幅，不同初相角而频率成整数倍关系的一些正弦量。A1cos(ω1t+ψ1)项称为一次谐波或基波，A1，ψ1分别为其振幅和初相角；A2cos(ω2t+ψ2)项的角频率为基波角频率ω1的2倍，称为二次谐波，A2，ψ2分别为其振幅和初相角；其余的项分别称为三次谐波，四次谐波等。基波，三次谐波，五次谐波……统称为奇次谐波；二次谐波，四次谐波……统称为偶次谐波；除恒定分量和基波外，其余各项统称为高次谐波。式（10-2-1）说明一个非正弦周期函数可以表示一个直流分量与一系列不同频率的正弦量的叠加。
　　上式有可改写为如下形式，即
　　当A0，An, ψn求得后，代入式 (10-2-1)，即求得了非正弦周期函数f(t)的傅里叶级数展开式。
　　把非正弦周期函数f(t)展开成傅里叶级数也称为谐波分析。工程实际中所遇到的非正弦周期函数大约有十余种，它们的傅里叶级数展开式前人都已作出，可从各种数学书籍中直接查用。
　　从式（10-2-3）中看出，将n换成(-n)后即可证明有
　　a-n=an
　　b-n=-bn
　　A-n=An
　　ψ-n=-ψn
　　即an和An是离散变量n的偶函数，bn和ψn是n的奇函数。
　　二． 傅里叶级数的复指数形式
　　将式（10-2-2）改写为
　　可见 与 互为共轭复数。代入式（10-2-4）有
　　上式即为傅里叶级数的复指数形式。
　　下面对和上式的物理意义予以说明：
　　由式（10-2-5）得的模和辐角分别为
　　可见的模与幅角即分别为傅里叶级数第n次谐波的振幅An与初相角ψn，物理意义十分明确，故称为第n次谐波的复数振幅。
　　的求法如下：将式（10-2-3a,b）代入式（10-2-5）有
　　上式即为从已知的f(t)求的公式。这样我们即得到了一对相互的变换式（10-2-8）与（10-2-7），通常用下列符号表示，即
　　即根据式（10-2-8）由已知的f(t)求得，再将所求得的代入式（10-2-7），即将f(t)展开成了复指数形式的傅立叶级数。
　　在（10-2-7）中，由于离散变量n是从（-∞）取值，从而出现了负频率（-nω1）。但实际工程中负频率是无意义的，负频率的出现只具有数学意义，负频率（-nω1）一定是与正频率nω1成对存在的，它们的和构成了一个频率为nω1的正弦分量。即
　　引入傅立叶级数复指数形式的好处有二：（1）复数振幅同时描述了第n次谐波的振幅An和初相角ψn；（2）为研究信号的频谱提供了途径和方便。
　　高等数学中的傅立叶级数
　　傅立叶系数
　　傅立叶系数包括系数 ，积分号和它的积分域，以及里面的两个周期函数的乘积——其中一个是关于f的，另一个是关于x的函数f(x),另一个则是和级数项n有关的三角函数值。这个三角函数可以是正弦，也可以是余弦，因此傅立叶系数包括正弦系数和余弦系数。其中当n=0时，余弦值为1，此时存在一个特殊的系数 ，它只与x有关。正弦系数再成一个正弦，余弦再乘一个余弦，相加并且随n求和，再加上一半的 ，就称为了这个特别的函数f(x)的傅立叶级数。为什么它特别呢，我想因为这里只有它只限于一个周期函数而已，而级数的周期就是f(x)的周期，2 。
　　如果函数f(x)存在一个周期，但是不是2 了，而是关于y轴对称的任意一个范围，它还能写成傅立叶级数么？也可以的。只要把傅立叶系数里的 换成l，并且把积分号里的三角函数中的n 下除一个l，同时把系数以外的那个n 底下也除一个l。其他的都不动。也可以认为，2 周期的傅立叶级数其实三角函数中x前面的系数应该是 ，其他的 （积分域和系数）应该是x，只不过这时所有的l都是 罢了。
　　前面提及了，周期或是积分域，是关于y轴的一个任意范围。其实周期函数不用强调这个，但是为什么还要说呢？因为要特别强调一下定义域是满的。有些函数的定义域不是满的，是0到l，当然这样它有可能不是周期的。这些函数能写成傅立叶级数么？同样可以。而且，它的写法不再是正弦和余弦函数的累积，而是单独的一个正弦函数或是余弦函数。具体怎么写，就取决于怎么做。因为域是一半的，所以自然而然想到把那一半补齐，f就成了周期函数。补齐既可以补成奇函数也可以补成偶函数。补成积函数，写成的级数只有正弦项，即 为0。补成偶函数，写成的级数就只含有余弦项和第一项，即 为0。而，傅立叶系数相比非积非偶的函数要大一倍。
　　其实，如果不经延拓，上面那些对于奇偶函数同样使用。
　　在做题时，常常看到级数后面跟着一个系数还有一个正弦函数，然后后面给出了这个系数很复杂的一串式子，这时候就容易突然短路了。但是如果再定睛一看，会发现其实那个系数不过是一个有积分的傅立叶系数而已。那么一大串，应该看什么呢？应当先看积分域，一下就可以定出周期了。第二步要明确级数和函数的关系即等价关系。函数不但包含在级数中，而且函数本身也是和级数等价的。但一般那个级数里的函数是一个摆设，不起什么作用