数据结构学习笔记——线索二叉树
Posted 晚风(●•σ )
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构学习笔记——线索二叉树相关的知识,希望对你有一定的参考价值。
目录
一、线索二叉树的结点结构
在由n个结点组成的二叉链表中,含有n+1个空指针域,含有n-1个非空指针域。
如前面文章介绍的,含有n个结点的二叉树中,有n+1个空指针,对于叶子结点,它有两个空指针;对于度为1的结点(只有一个子结点),它只有一个空指针。将这些空指针利用起来,例如可以让其存放指向该结点的前驱或后继,从而使遍历二叉树更加简便,加快查找结点的前驱或后继的速度,即线索二叉树,由于线索二叉树是加上线索的链表结构,是计算机内部的一种存储结构,是一种物理结构。
- 另外,由于有n个结点,即有链域指针2n个,除了根结点以外,每个结点都被一个指针所指向,剩余的链域建立线索,即n个结点的线索二叉树含义的线索数为2n-(n-1)=
n+1个。
- 线索二叉树也分为前序线索二叉树、中序线索二叉树以及后序线索二叉树,即它们都是对二叉树中的所有结点的空指针进行某种遍历方式加线索,指向结点前驱和后继的指针称为
线索。
线索二叉树的结点结构如下:
| lchild | ltag | data | rtag | rchild |
|---|
其中ltag和rtag是标识域,用于区分线索指针和原本指向孩子结点的指针,不同标识域代表不同含义,我们规定如下:
| ltag | 含义 |
|---|---|
| 0 | lchild指针,指向结点的左孩子 |
| 1 | lchild线索,指向结点的直接前驱 |
| rtag | 含义 |
|---|---|
| 0 | rchild指针,指向结点的右孩子 |
| 1 | rchild线索,指向结点的直接前驱 |
同理,先序线索二叉树和后序线索二叉树也是一样的,将原本的二叉树进行线索化。
注:虽然二叉树线索化后,但在先序线索二叉树中仍不能有效求解找到前驱结点,在后序线索二叉树中也不能有效求解找到后驱结点,需要通过其他方法解决,如下表:
| 操作 | 中序线索二叉树 | 先序线索二叉树 | 后序线索二叉树 |
|---|---|---|---|
| 找前驱结点 | √ | × | √ |
| 找后继结点 | √ | √ | × |
二、线索二叉树的定义
线索二叉树的定义代码如下:
/*线索二叉树的定义*/
typedef struct CLTNode
char data;
int ltag,rtag; //标识域
struct CLTNode *lchild,*rchild;
CLTNode,*CLTree;
三、中序线索二叉树的遍历
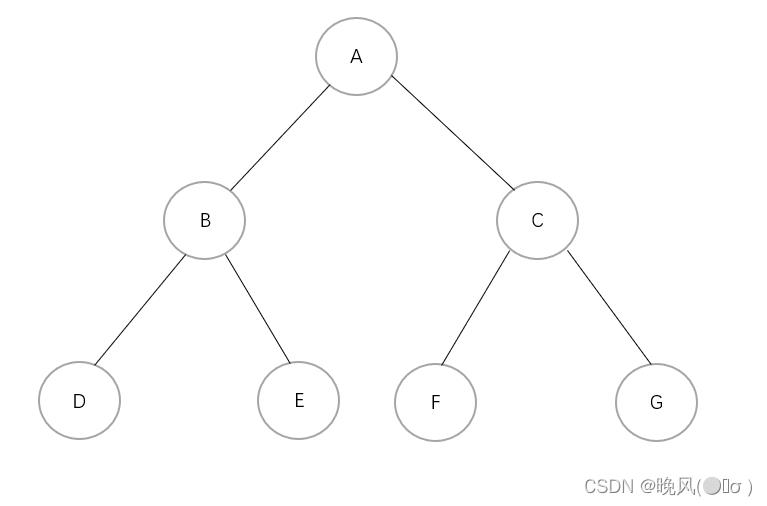
如下图,由中序遍历序列(DBEAFCG)可以推出,其中结点D和结点G的中序前驱和中序后继为NULL,若ltag=1,lchild为线索,指向结点的直接前驱,否则该结点的前驱是以该结点为根结点的左子树按中序遍历的最后一个结点;若rtag=1,rchild为线索,指向结点的直接后继,否则该结点的后继是以该结点为根结点的右子树按中序遍历的第一个结点:
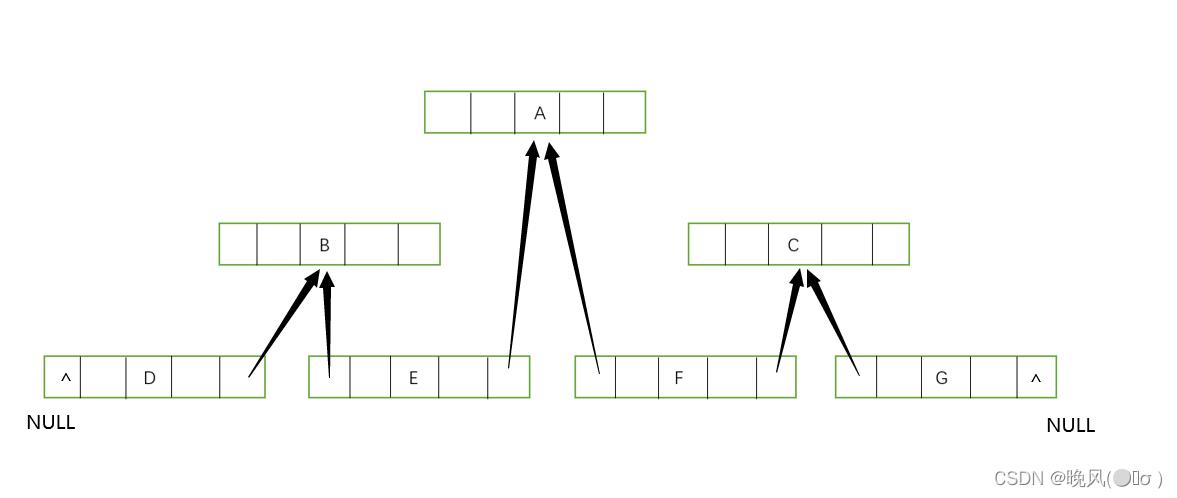
如下图:

指针p指向当前访问结点,以指针pre指向刚访问过的结点,例如对一个结点,检查p的左指针是否为空,若为空则将其指向指针pre,然后递归遍历右子树;检查pre的右指针是否为空,若为空则将其指向指针p,依次进行下去。
/*中序线索二叉树的遍历*/
void InTree2(CLTNode *p,CLTNode *&pre)
if(p!=NULL)
InTree2(p->lchild,pre); //递归,左子树线索化
if(p->lchild==NULL) //若左子树为空
p->lchild=pre; //建立前驱线索,使pre指向p的直接前驱
p->ltag=1; //将当前结点的ltag置为1,标识为线索,指向结点的直接前驱
if(pre!=NULL&&pre->rchild==NULL) //若左子树不为空,且右子树为空
pre->rchild=p; //建立后驱线索 ,使p指向pre的直接后驱
pre->rtag=1; //将当前结点的rtag置为1,标识为线索,指向结点的直接后驱
pre=p; //pre指向p
InTree2(p->rchild,pre); //p指向下一个结点,递归,右子树线索化
四、先序线索二叉树的遍历
先序线索二叉树的遍历代码在中序的代码基础上,将连接线索的代码放在左右子树递归线索化的前面,若要查找一个结点的先序后继。
/*先序线索二叉树的遍历*/
void ProTree2(CLTNode *p,CLTNode *&pre)
if(p!=NULL)
if(p->lchild==NULL) //若左子树为空
p->lchild=pre; //建立前驱线索,使pre指向p的直接前驱
p->ltag=1; //将当前结点的ltag置为1,标识为线索,指向结点的直接前驱
if(pre!=NULL&&pre->rchild==NULL) //若左子树不为空,且右子树为空
pre->rchild=p; //建立后驱线索 ,使p指向pre的直接后驱
pre->rtag=1; //将当前结点的rtag置为1,标识为线索,指向结点的直接后驱
pre=p; //pre指向p
if(p->ltag==0)
ProTree2(p->lchild,pre); //递归,左子树线索化
if(p->rtag==0)
ProTree2(p->rchild,pre); //递归,右子树线索化
五、后序线索二叉树的遍历
而后序线索二叉树的遍历代码也在中序的代码基础上,将连接线索的代码放在左右子树递归线索化的后面。
/*后序线索二叉树的遍历*/
void PostTree2(CLTNode *p,CLTNode *&pre)
if(p!=NULL)
PostTree(p->lchild,pre); //递归,左子树线索化
PostTree(p->rchild,pre); //递归,右子树线索化
if(p->lchild==NULL) //若左子树为空
p->lchild=pre; //建立前驱线索,使pre指向p的直接前驱
p->ltag=1; //将当前结点的ltag置为1,标识为线索,指向结点的直接前驱
if(pre!=NULL&&pre->rchild==NULL) //若左子树不为空,且右子树为空
pre->rchild=p; //建立后驱线索 ,使p指向pre的直接后驱
pre->rtag=1; //将当前结点的rtag置为1,标识为线索,指向结点的直接后驱
pre=p; //pre指向p
总结
简单的来说,若要画出二叉树的先/中/后序线索二叉树,只需经过以下几个步骤:
1、首先求出要画的相应线索二叉树的先/中/后序遍历序列;
2、画线索(针对二叉树中缺少左、右孩子的结点):
(1)若该结点无左孩子,则线索指向相应线索二叉树的先/中/后序遍历序列的前驱,若无前驱则指向NULL;
(2)若该结点无右孩子,则线索指向相应线索二叉树的先/中/后序遍历序列的后继,若无后继则指向NULL。
以下面这个二叉树为例,画出其中序线索二叉树。
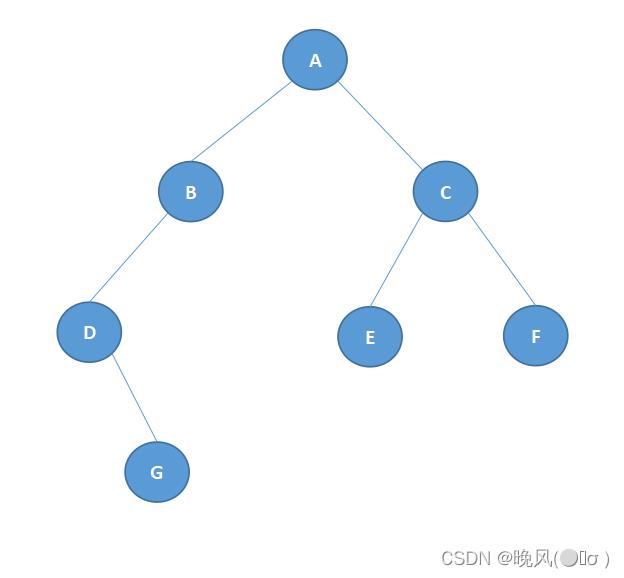
1、求出其中序遍历序列为DGBAECF;
2、对于二叉树中缺少左、右孩子的结点B、D、G、E、F,画出线索:
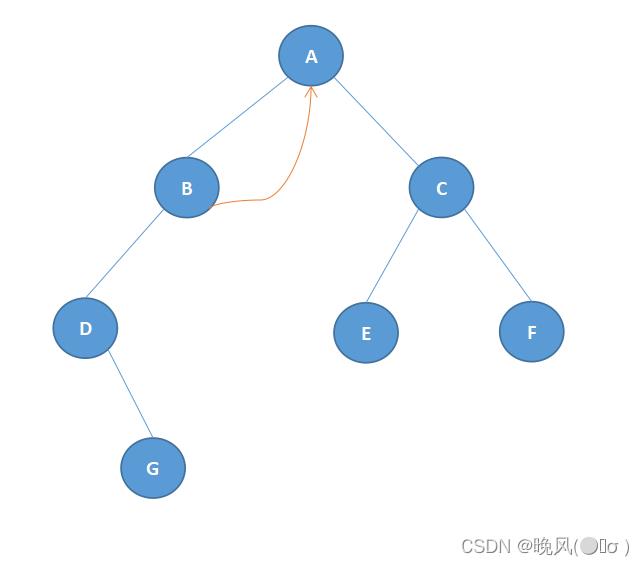
对于结点B,缺少右孩子,其线索指向中序遍历序列中B的后继结点A,如下:
对于结点D,缺少左孩子,其线索指向中序遍历序列中D的前驱结点,由于中序遍历序列中前驱无结点,即指向NULL,如下:
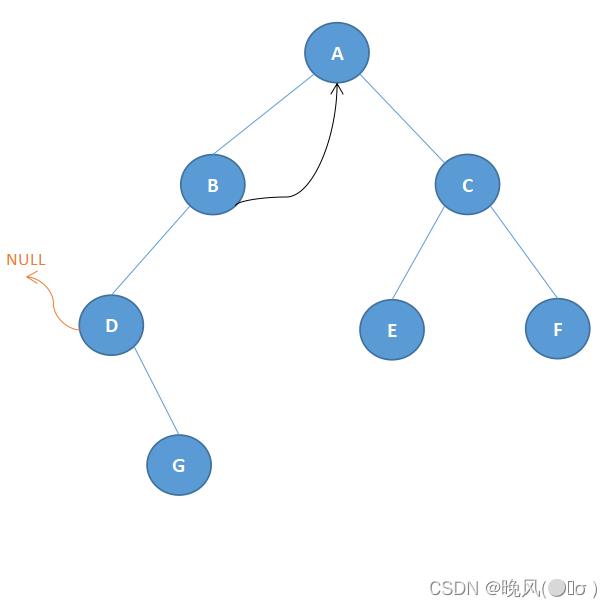
对于结点G,缺少左右孩子,其一条线索指向中序遍历序列中G的后继结点B和一条线索指向中序遍历序列中G的前驱结点D,如下:

对于结点E和F,也是缺少左右孩子,如下:
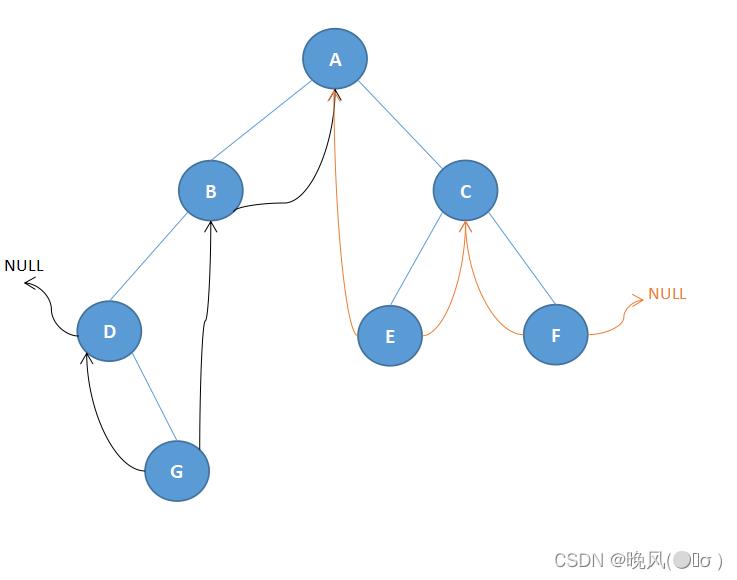
最终,得到的中序线索二叉树如下:
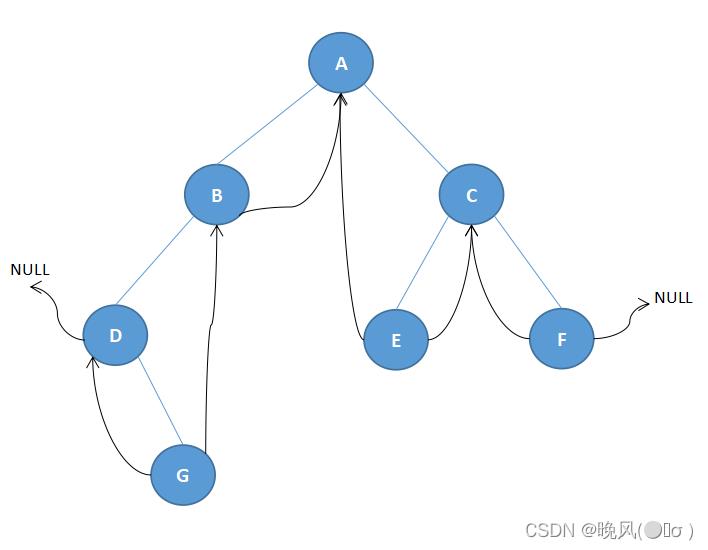
以上是关于数据结构学习笔记——线索二叉树的主要内容,如果未能解决你的问题,请参考以下文章