激光SLAM入门：坐标变换

Posted 2023-02-02 lsldd

0、 预备知识：齐次坐标

齐次坐标是整个系列的基础。如果不理解齐次坐标系的概念，强烈建议先阅读https://zhuanlan.zhihu.com/p/74597564

1、机器人位姿表示

二维情况下，机器人的位姿可以用（x，y，θ）来表示。注意此处θ为顺时针的旋转角度。在图形学中，右手坐标系中旋转以逆时针为正。然而SLAM中默认以比较贴近生活的顺指针为正，这个很容易混淆。
假设世界坐标系W，机器人坐标系为A，机器人在坐标系W中的坐标为（x，y，θ），则机器人坐标系A到世界坐标系W的转换矩阵为$T_A^W$ 。也就是说，如果已知机器人A坐标系表示的点$P_A$，则该点在世界坐标系中的坐标为 $P_W=T_A^W{P}_A$。其中：

仔细观察这个矩阵会发现，这不就是逆时针旋转θ（顺时针旋转-θ），再平移t的矩阵变换吗！
那么同样的，要得到世界坐标系W到机器人坐标系A的转换矩阵，只需要将矩阵求逆即可（注意R是正交矩阵，有$R^{-1}=R^T$）：
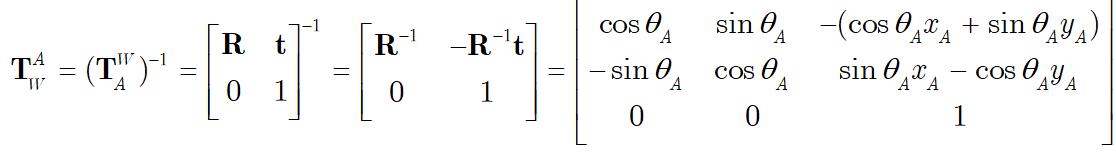所以，这一部分最重要的收获是：所谓B坐标系到A坐标系的表示，实际上就是一个矩阵变换$T_B^A$ 。

2、相对坐标转换

考虑机器人发生了旋转、平移运动到了新的坐标系B，在W中的坐标为（x，y，θ）。同理我们有：

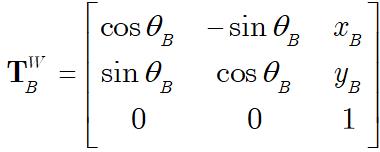
在实际应用中，我们更希望知道：A是通过什么样的变换方式（实质就是一个矩阵）变换到B的？例如说，在A的自身坐标系中右转90度、前进1米，到达B，这样显然更有意义。也就是说，我们希望求出 $T_A^B$ 。
显然，我们已知B在W中的表示 ，那么再将其做一次转换，求其在A坐标系中的表示不就行了吗？即：

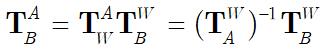
在上一节我们已经求出了$T_W^A$ 。带入上式可得：

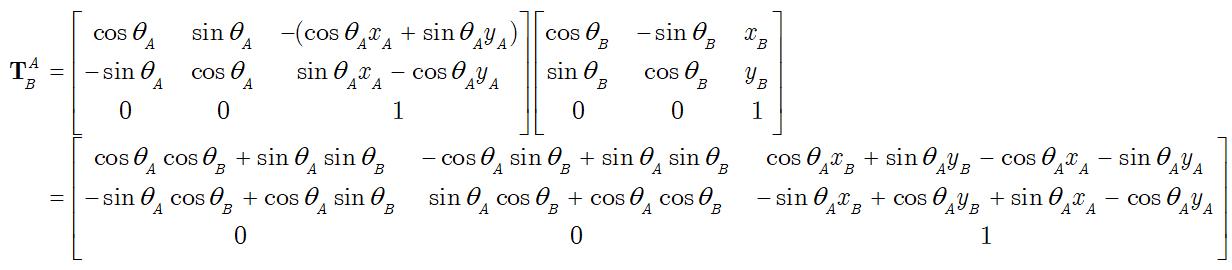
这个矩阵看上去非常复杂，实际上考虑到三角函数公式，可以化简如下：

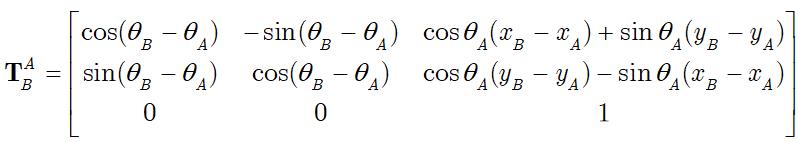
矩阵中的R部分为A到B的旋转变化，这很好理解。如何理解这复杂的t部分呢？

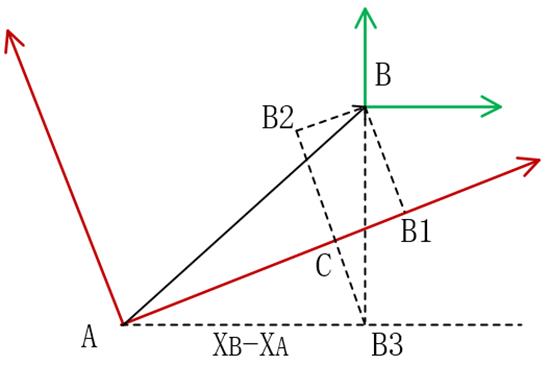
如图所示，红色为A坐标系（原点设为A），绿色为B坐标系（原点设为B）。 $T_B^A$ 中的t的本质是向量AB在A坐标系中的表示。因此考虑将B投影到A的x轴（图中B1），将B沿世界坐标系的Y轴做延长线，A在沿世界坐标系的X轴做延长线，交点计为B3。B3再沿A坐标系的Y轴做延长线，B点沿A坐标系的X轴做延长线，交点计为B2。B2-B3与A坐标系X轴交于C。
此时，B在A坐标系X方向的投影长度为|AC|+|CB1|。观察直角三角形△ACB3、△BB2B3，容易得知：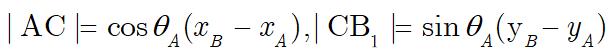
刚好得到$T_B^A$ 中t的x偏移值。这可不是巧合！
同样的方法也可以求出t的y偏移值。只不过此时，B在A坐标系Y方向的投影长度为|AC|-|CB1|。

同时你会发现，t的结果跟B的旋转角度没有关系。
这就是坐标系B在坐标系A中表示的矩阵的几何意义。