机器学习之求解无约束最优化问题方法(手推公式版)

Posted 2023-02-01 夏小悠

文章目录

• • 前言
  • 1. 基础知识
  • • 1.1 方向导数
    • 1.2 梯度
    • 1.3 方向导数与梯度的关系
    • 1.4 泰勒展开公式
    • 1.5 Jacobian矩阵与Hessian矩阵
    • 1.6 正定矩阵
  • 2. 梯度下降法
  • 3. 牛顿法
  • 4. 拟牛顿法
  • 5. 代码实现
  • 结束语

前言

  本篇博文主要介绍了机器学习里面的常见的求解无约束最优化问题的方法，包括梯度下降法、牛顿法和拟牛顿法，并给出了相关的推导过程及代码实现。

  本篇博文内容主要来自李航老师的《统计学习方法》（附录A和B）。

1. 基础知识

1.1 方向导数

  在许多问题中，我们不仅要知道函数再坐标轴上的变化率（即偏导数），而且还要设法求得函数在某点沿着其他特定方向上的变化率，这就是方向导数。
  方向导数的计算公式如下：设三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$处可微分，则$u=u(x,y,z)$在点$P_0$处沿任一方向 $\mathbf{l}$ 的方向导数都存在，则

1.2 梯度

  在一个数量场中，函数在给定点处沿不同的方向，其方向导数一般都是不相同的，现在我们关心的是沿哪一个方向其方向导数最大？最大值是多少？函数在点$P$沿哪一个方向增加的速度最快？由此引入了梯度这一概念。
  设三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$处具有一阶偏导数，则定义$$\mathbf{grad}u{|}_{P_0}=(u_x^{\prime }(P_0),u_y^{\prime }(P_0),u_z^{\prime }(P_0))$$  为函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$处的梯度。

1.3 方向导数与梯度的关系

  由方向导数的计算公式和梯度的定义可以得到

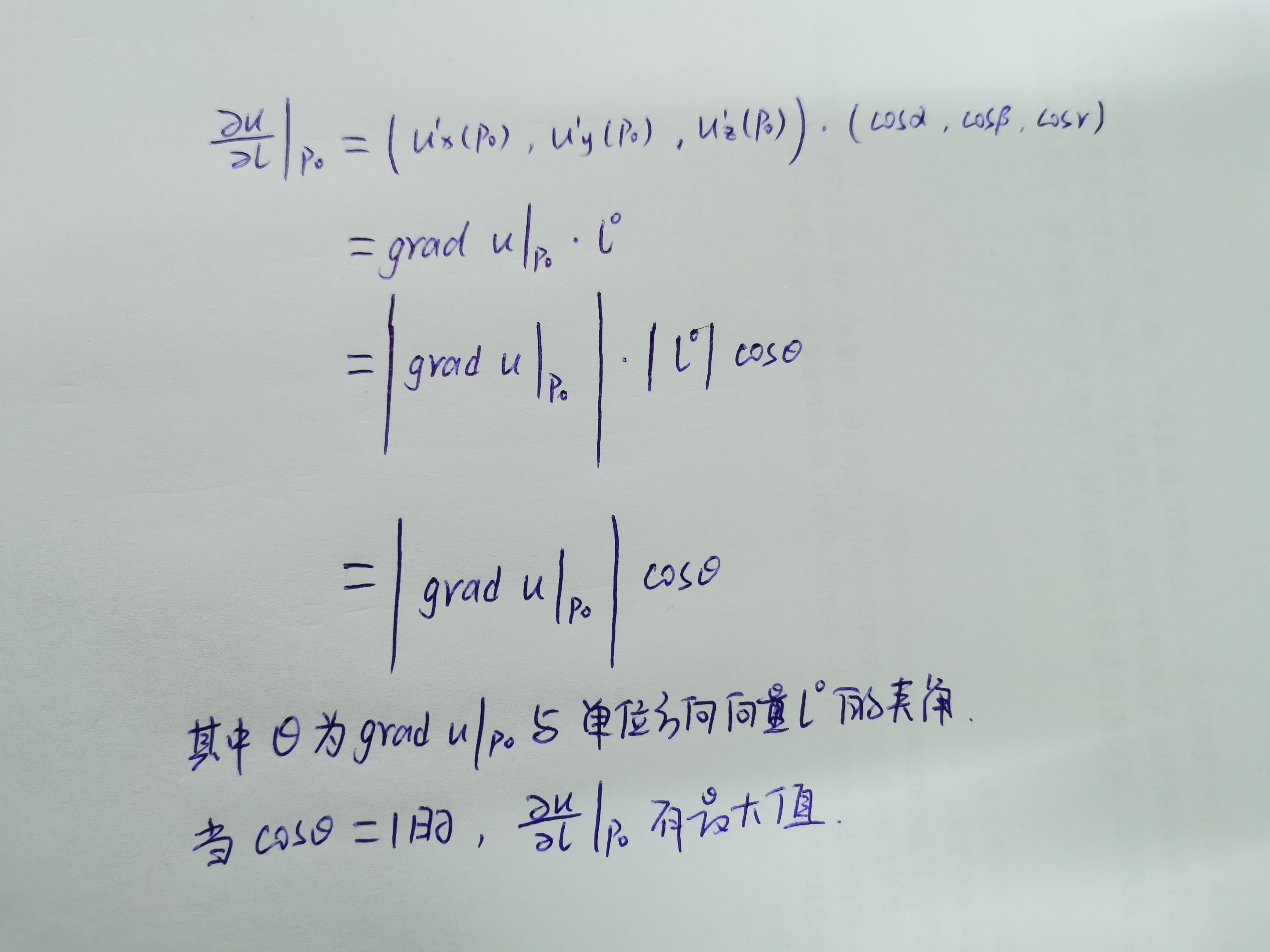
  由上可以得到如下结论：函数在某点的梯度是一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值，再通俗点说，梯度的方向就是变化率最快的方向，也就是函数值增加最快的方向。

1.4 泰勒展开公式

  设$f(x)$在点$x_0$的某个邻域内n+1阶导数存在，则对该邻域内的任意点有$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{1}{2}{f}^{\prime \prime }(x_0)(x-x_0{)}^2+\cdots +\frac{1}{n!}{f}^{(n)}(x_0)(x-x_0{)}^n+\frac{1}{(n+1)!}{f}^{(n+1)}(\xi )(x-x_0{)}^{(n+1)}$$  其中$\xi$介于$x$和$x_0$之间。
  上述公式是带拉格朗日余项的n阶泰勒公式，当$x_0=0$时，上述泰勒公式又称为麦克劳林公式。

1.5 Jacobian矩阵与Hessian矩阵

  简单来说，由一阶偏导数组成的矩阵叫做Jacobian矩阵(雅可比矩阵)，由二阶偏导数组成的矩阵叫做Hessian矩阵(黑塞矩阵)。
  称矩阵 J = [ ∂ f 1 ∂ x 1 ∂ f 1 ∂ x 2 … ∂ f 1 ∂ x n ∂ f 2 ∂ x 1 ∂ f 2 ∂ x 2 … ∂ f 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ f n ∂ x 1 ∂ f n ∂ x 2 … ∂ f n ∂ x n ] J=\\beginbmatrix \\frac \\partial f_1 \\partial x_1 & \\frac \\partial f_1 \\partial x_2 & \\dots & \\frac \\partial f_1 \\partial x_n \\\\[5pt] \\frac \\partial f_2 \\partial x_1 & \\frac \\partial f_2 \\partial x_2 & \\dots &\\frac \\partial f_2 \\partial x_n \\\\ \\vdots & \\vdots & \\ddots & \\vdots \\\\[3pt] \\frac \\partial f_n \\partial x_1 & \\frac \\partial f_n \\partial x_2 & \\dots & \\frac \\partial f_n \\partial x_n \\endbmatrix J= ​∂x1​∂f1​​∂x1​∂f2​​⋮∂x机器学习之支持向量机(手推公式版)

机器学习之支持向量机(手推公式版)

机器学习之主成分分析(手推公式版)

运筹学（最优化理论）学习笔记 | 共轭梯度法

手推机器学习 吴恩达 神经网络BP反向传播 示例推导（下篇）

百度面试——机器学习