二叉树和哈希表的优缺点对比与选择

Posted 2023-05-03

参考技术A 二叉树(binary tree)和哈希表(hash table)都是很基本的数据结构，但是我们要怎么从两者之间进行选择呢？他们的不同是什么？优缺点分别是什么？

回答这个问题不是一两句话可以说清楚的，原因是在不同的情况下，选择的依据肯定也不同。首先来回顾一下这两个数据结构：

哈希表使用hash function来对输入的数据分配index到哈希表对应的槽中。假设有一个哈希表的size是100，而我们输入的数据是从0～99，我们要把输入数据储存到哈希表中。理论上来说，该哈希表插入和查找操作的时间复杂度都是O(1)。

二叉树遵循右子树大于根节点，左子树小于根节点的原则进行数据的插入和保存。如果这个树的平衡的，那么，对于每个元素的插入和查找操作的时间复杂度是O(log(n))，n是树的节点个数，log(n)通常是树的深度。当然，对于不平衡的情况，那就需要更复杂的数据结构的树（红黑树等）进行处理。

上文似乎得出结论哈希表要好于二叉树，但是it is not always the case。哈希表有以下几个突出的缺点：

另一方面，我们讨论二叉树：

如果你预先知道输入数据的大小，而且有足够的空间储存哈希表，且不需要对数据进行排序，那么哈希表总是好的。因为哈希表在插入，查找和删除操作中只需要常数时间。

另一方面，如果数据是持续的加入，你预先不知道数据的大小，那么二叉树是一个折中的选择。

细说二叉树

为了后续学习堆排序以及MySQL索引等知识，接下来会重温一下树这种数据结构，包括二叉树、赫夫曼树、二叉排序树(BST)、平衡二叉树(AVL)、B树和B+树。本文只涉及二叉树，其他树后续再细说。

一、树的介绍

「1. 为什么要有树这种结构？」

有了数组和链表，为什么还要有树？先来看看数组和链表的优缺点。

• 数组：因为有索引，所以可以快速地访问到某个元素。但是如果要进行插入或者删除的话，被插入/删除位置之后的元素都得移动，如果插入后超过了数组容量，还得进行数组扩容。可见，数组查询快，增删慢。

• 链表：没有索引，要查询某个元素，得从第一个元素开始，一个一个往后遍历。但是要进行插入或者删除，无需移动元素，只要找到插入/删除位置的前一个元素即可。所以链表查询慢，增删快。

说到这里，那肯定知道树存在的意义了，没错，它吸收了链表和数组的优点，查询快，增删也快。

「2. 二叉树：」

每个节点最多有两个叶子节点的树，叫做二叉树。假如一棵树有n层，所以的叶子节点都在第n层，并且节点总数为(2^n) - 1，那么就把这棵树称为「满二叉树」。如果最后一层的叶子节点左边是连续的，倒数第二层右边的叶子节点是连续的，那就称为「完全二叉树」。

二、二叉树的遍历

前序遍历、后序遍历和中序遍历，这里的前中后指的是父节点的遍历时机。

• 前序遍历：根左右。先输出当前节点；如果左子节点不为空，则递归进行前序遍历；如果右子节点不为空，则继续递归前序遍历。

• 中序遍历：左根右。如果左子节点不为空，则递归中序遍历；输出当前节点；如果右子节点不为空，则递归中序遍历。

• 后序遍历：左右根。如果左子节点不为空，递归后序遍历；如果右子节点不为空，递归后序遍历；输出当前节点。

「1. 新建一个TreeNode类：」

这个是节点类，省略了set/get方法。

public class TreeNode {
 
 private Object element;
 private TreeNode left;
 private TreeNode right;
 
    public TreeNode() {}
    public TreeNode(Object element) {
     this.element = element;
    }
}

「2. 构建一棵二叉树：」

二叉树

假如要构建这样一棵树，那么代码实现就是：

TreeNode root = new TreeNode(6);
TreeNode node1 = new TreeNode(5);
TreeNode node2 = new TreeNode(4);
root.setLeft(node1);
root.setRight(node2);
TreeNode node3 = new TreeNode(3);
node1.setLeft(node3);
TreeNode node4 = new TreeNode(2);
node1.setRight(node4);
TreeNode node5 = new TreeNode(1);
node2.setLeft(node5);

按照遍历规则，前中后序的遍历结果应该是：

• 前序遍历： 6, 5, 3, 2, 4, 1
• 中序遍历： 3, 5, 2, 6, 1, 4
• 后序遍历： 3, 2, 5, 1, 4, 6

「3. 代码实现三种遍历方式：」

/**
 * 前序遍历
 * 
 * @param root
 */
public static void preOrder(TreeNode root) {
 // 先输出当前节点
 System.out.println(root.getElement());
 // 判断左子节点是否为空，不为空就递归
 if (root.getLeft() != null) {
  preOrder(root.getLeft());
 }
 // 判断右子节点是否为空，不为空就递归
 if (root.getRight() != null) {
  preOrder(root.getRight());
 }
}

/**
 * 中序遍历
 * 
 * @param root
 */
public static void infixOrder(TreeNode root) {
 // 判断左子节点是否为空，不为空就递归
 if (root.getLeft() != null) {
  infixOrder(root.getLeft());
 }
 // 输出当前节点
 System.out.println(root.getElement());
 // 判断右子节点是否为空，不为空就递归
 if (root.getRight() != null) {
  infixOrder(root.getRight());
 }
}

/**
 * 后序遍历
 * @param root
 */
public static void postOrder(TreeNode root) {
 // 判断左子节点是否为空，不为空就递归
 if (root.getLeft() != null) {
  postOrder(root.getLeft());
 }
 // 判断右子节点是否为空，不为空就递归
 if (root.getRight() != null) {
  postOrder(root.getRight());
 }
 // 输出当前节点
 System.out.println(root.getElement());
}

二叉树的查找就不说了，都会遍历了还不会查找吗？

三、二叉树的删除

这里说的删除先不考虑子节点上浮的情况，即如果删除的非叶子节点，那就直接删除整棵子树。删除的思路如下：

• 如果二叉树只有一个节点，直接将该节点设置为null即可；
• 判断当前节点的左子节点是否为要删除的节点，如果是，就删除当前节点左子节点；
• 判断当前节点的右子节点是否为要删除的节点，如果是，就删除当前节点右子节点；
• 如果上述操作没有找到要删除的节点，就向当前节点左子树递归；
• 如果向左子树递归也没找到要删除的节点，就向当前节点右子树递归；

「代码实现：」

/**
* 删除节点
* @param node
*/
public static void delNode(TreeNode root, Object ele) {
 // 如果二叉树为空，直接return
 if (root == null) {
  return;
 }
 // 如果只有一个节点，或者root就是要删除的节点，直接置空
 if ((root.getLeft() == null && root.getRight() == null) ||
   root.getElement() == ele) {
  root.setElement(null);
  root.setLeft(null);
  root.setRight(null);
  return;
 }
 // 判断左子节点是否为要删除的节点
 if (root.getLeft() != null && root.getLeft().getElement()== ele) {
  root.setLeft(null);
  return;
 }
 // 判断右子节点是否为要删除的节点
 if (root.getRight() != null && root.getRight().getElement()== ele) {
  root.setRight(null);
  return;
 }
 // 向左子树递归
 if (root.getLeft() != null) {
  delNode(root.getLeft(), ele);
 }
 // 向右子树递归
 if (root.getRight() != null) {
  delNode(root.getRight(), ele);
 }
}

四、顺序存储二叉树

所谓顺序存储二叉树，就是将二叉树的元素用数组存起来，并且在数组中遍历这些元素时依旧能体现出前/中/后序遍历。为了达到这个目的，所以顺序存储二叉树有一些要求：

• 通常只考虑完全二叉树；

我们给二叉树的元素从上到下从左往右从0开始依次标上号，这些号得满足：

• n号元素的左节点标号为 2n + 1；
• n号元素的右节点标号为 2n + 2；
• n号元素的父节点标号为 (n-1) / 2；

怎么将二叉树用数组存起来就不说了，进行层序遍历就好了，从上到下从左往右将元素依次存进数组。主要来看一看，用数组保存起来的二叉树。如何遍历，才能达到二叉树前/中/后序遍历的效果。

「代码实现：」

/**
* 前序遍历顺序存储的二叉树
* @param arr
*/
public static void preOder(int[] arr) {
 if (arr == null || arr.length == 0) {
  return;
 }
 preOder(arr, 0);
}
 
/**
* 前序遍历顺序存储的二叉树
* @param index
*/
private static void preOder(int[] arr, int index) {
 // 输出当前元素
 System.out.println(arr[index]);
 // 向左递归
 if ((index * 2 + 1) < arr.length) {
  preOder(arr, (index * 2 + 1));
 }
 // 向右递归
 if ((index * 2 + 2) < arr.length) {
  preOder(arr, (index * 2 + 2));
 }
}

这就是实现前序遍历的代码，中/后序遍历就换一下输出当前元素的位置就可以了。

五、线索化二叉树

二叉树

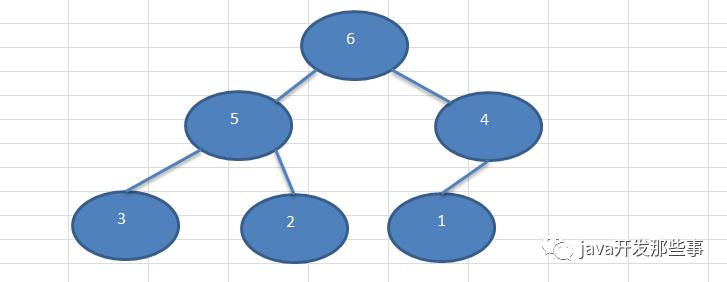
还是拿这棵二叉树来说，3，2，1节点的left和right指针都没用到，4节点的right指针没有用到，也就是整棵二叉树有7个指针是没有用到的。其实我们可以充分利用这些指针，让这些指针指向前/中/后序遍历的前/后一个节点，这就叫「线索化二叉树」。根据指针指向的不同节点，又可以分为前/中/后序线索化二叉树。

注意，要线索化二叉树，得满足一个条件，假如总共有n个节点，那么未使用的指针数应为n + 1。一个节点的前一个节点称为前驱节点，后一个节点称为后继节点。

「1. 中序线索化二叉树：」

上面这棵二叉树，中序遍历的结果是：3, 5, 2, 6, 1, 4，我们让有空闲指针的节点，left指针指向它的前驱，right指针指向它的后继。首先从3开始，3没有前驱，后继是5，所以3的right指针指向5；然后是2，让它left指向5，right指向6；1的left指向6，right指向4。中序线索化的二叉树如下图(绿色是左指针，黄色是右指针)：

中序线索化二叉树

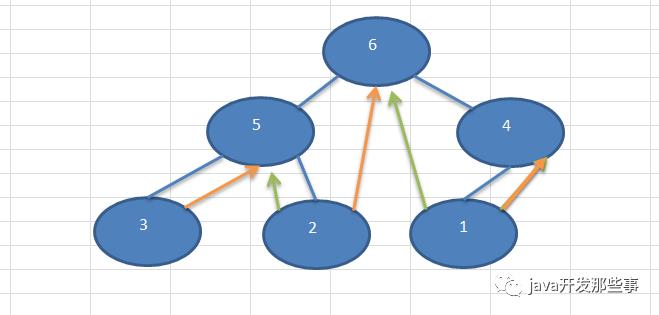
• 线索化二叉树后， left指针可能指向的是左子树，也可能指向前驱节点；
• right指针可能指向右子树，也可能指向后继节点；

「2. 代码实现：」

首先，对于TreeNode节点类，得增加两个属性，用来表示左右节点的类型，约定用0表示子树，用1表示前驱/后继。改造后的节点类如下：

public class TreeNode {
 private Object element;
 private TreeNode left;
 private TreeNode right;
 private int leftType; // 0左子树， 1前驱节点
 private int rightType; // 0右子树，1后继节点
}

上面所有操作二叉树的方法，我都封装在TreeUtil中，要线索化二叉树，还需要在TreeUtil中定义一个变量，用来保存前一个节点，如下：

private static TreeNode preNode; // 前一个节点

线索化二叉树的代码：

public static void inSeqLineTree(TreeNode curNode) {
  if (curNode == null){
            return;
        }
        // 处理左子树
        inSeqLineTree(curNode.getLeft());

        // 处理当前节点
        if (curNode.getLeft() == null){
            curNode.setLeft(preNode);
            curNode.setLeftType(1);
        }
        if (preNode != null && preNode.getRight() == null){
            preNode.setRight(curNode);
            preNode.setRightType(1);
        }
        preNode = curNode;

        // 处理右子树
        inSeqLineTree(curNode.getRight());
}

那么怎么验证有没有线索化成功呢？如果成功的话，节点3的right应该是节点5，并且节点3的型是1；节点2的left是5，并且节点2的类型是1。

public static void main(String[] args) {
        TreeNode root = new TreeNode(6);
        TreeNode node1 = new TreeNode(5);
        TreeNode node2 = new TreeNode(4);
        root.setLeft(node1);
        root.setRight(node2);
        TreeNode node3 = new TreeNode(3);
        node1.setLeft(node3);
        TreeNode node4 = new TreeNode(2);
        node1.setRight(node4);
        TreeNode node5 = new TreeNode(1);
        node2.setLeft(node5);

        TreeUtil.inSeqLineTree(root); // 6, 5, 3, 2, 4, 1

        System.out.printf("节点3的right：%s, 类型：%s %n", node3.getRight().getElement(), node3.getRightType());
        System.out.printf("节点2的left：%s, 类型：%s %n", node4.getLeft().getElement(), node4.getLeftType());
}

运行结果

结果和预期一致，说明线索化成功。

六、遍历线索化二叉树

上面线索化了二叉树，有什么用呢？其实就是为了可以更简单地进行遍历。线索化之后，各个节点的指向有变化，所以原来的遍历方式就用不了了，现在可以用非递归的方式进行遍历，可以提高效率。

遍历线索化二叉树的代码：

public static void seqOrder(TreeNode root) {
  TreeNode curNode = root;
  while(curNode != null) {
   // 找到leftType为1的节点
   while(curNode.getLeftType() == 0) {
    curNode = curNode.getLeft();
   }
   // 找到就输出
   System.out.println(curNode.getElement());
   // 如果当前节点的右指针指向的是后继节点，就直接输出
   while(curNode.getRightType() == 1) {
    curNode = curNode.getRight();
    System.out.println(curNode.getElement());
   }
   // 遇到了不等于1的，替换遍历的节点
   curNode = curNode.getRight();
  }
}

传入root后，运行结果是和中序遍历的结果一致的，说明没问题。

扫描二维码

获取更多精彩

java开发那些事