机器学习复现2.非递归法构造并搜索kd树

Posted 2023-01-19 天津泰达康师傅

kd树的目的：在特征空间的维数大及训练数据容量大时尤其必要。
kd树的构建，即划分各样本点对应的子区域
kd树的搜索，
(1)在kd树中找出包含目标点x的叶节点，即从根结点开始递归地向下访问kd树。若目标点x的当前维的坐标小于切分点的坐标，否则移动到右子结点，直到子节点为叶节点为止。
（2）更新当前找到的叶节点为”当前最近点“。
（3）递归向上回溯父节点，在每个结点执行以下操作：
（a)先判断该结点保存的实例点是否比当前最近点距离目标点更近，则以该实例点为”当前最近点“。
（b)检查该子节点的父节点的另一子结点对应的区域是否有更近的点。具体判断方式如下：
以目标点为球心，目标点与”当前最近点“之间的距离为半径做超球面。判断该超球面与另一子节点所对应的超平面是否有可能相交，如果相交，则需要递归查找另一子节点对应子区域内的所有点。如果不相交，继续向上回退。
（4）回退到根节点时，搜索结束。最后的当前最近点为x的最近邻点。
如果kd树节点中不记录父节点，可尝试利用栈进行回溯。

#!/usr/bin/env python
#-*- coding:utf-8 -*-
# @Time    : $DATE $TIME
# @Author  : yck

import numpy as np
from queue import Queue
import copy
import matplotlib.pyplot as plt

##训练集，如下例，特征空间维度为2。
train_dataset_x = np.random.randint(1,100,(10000,3))
# train_dataset_x = np.array([[2,3],
#                            [5,4],
#                             [9,6],
#                             [4,7],
#                             [8,1],
#                             [7,2]])

def kd_median(arr):
    ##返回的是样本索引索引，arr为抽取出来的各样本的第k维
    ##返回：分割的样本索引（中位数），左划分样本索引，右划分样本索引
    sorted_array = np.argsort(arr)
    return sorted_array[int((arr.size)/2)],sorted_array[:int((arr.size)/2)],sorted_array[int((arr.size)/2)+1:]

def kd_seq(train_dataset_x):
    ##按方差从大到小返回各特征索引，构造kd树时可以使用这一顺序
    ##比如某例子中，特征空间为3维，其方差从大到小为特征2，特征1，特征0，该函数就返回np.array([2 1 0])
    ##kd树中，按照此顺序选择每层分割实例对应的特征。第一层选取特征2，第二层选取特征1，第三层选取特征0，第四层选取特征2......以此类推
    kd_charc_var = np.var(train_dataset_x,axis=0)
    sorted_kd_charc_var = np.argsort(-kd_charc_var)
    return np.array([i for i in range(len(train_dataset_x[0]))])[sorted_kd_charc_var]

class kd_tree(object):
    ##以train_dataset_x样本点特征空间第0维[2 5 9 4 8 7]为例
    ##排序后为[2 4 5 7 8 9]
    split_instance = None   ##分割实例索引,中位数为7，split_instance返回其在[2 5 9 4 8 7]中的索引5
    charac_dim = None     ##结点所在层的分割维度,例子中分割维度为0
    left_instance = None    ##位于中位数以左的各样本索引,对应2，4，5的索引。返回np.array([0 3 1])
    right_instance = None       ##位于中位数以右的各样本索引,同上。
    left_child = None           ##左孩子指针，链接一个kd_tree对象
    right_child = None          ##右孩子指针，链接一个kd_tree对象
    has_visited = False         ##是否已回溯，初始设置为未访问，等一会儿回溯的时候用。


    def __init__(self,split_instance,charac_dim,level,left_instance,right_instance):
        '''
        kd_tree初始化函数
        :param split_instance: 分割样本
        :param charac_dim: 选取的特征维度
        :param level:
        :param left_instance:
        :param right_instance:
        '''
        self.split_instance = split_instance
        self.charac_dim = charac_dim
        self.level = level   ##从第零层开始
        self.left_instance = left_instance
        self.right_instance = right_instance


class k_neighbour(object):
    ##利用kd树实现最近邻算法
    p = 2   ##lp距离中，p=2对应欧几里得距离
    kd_tree = None     ##构造出来的kd树
    route = []  ##路径,里面装结点。
    segmentation_sample = None     ##求得的最邻近点
    low_dist = float("inf")               ##最短距离,初始为无穷大
    has_calculate = np.array([[]])

    def lp_dis(self,arr1,arr2):
        '''

        :param arr1:arr1样本
        :param arr2: arr2样本
        :return: 返回arr1和arr2样本的欧氏距离
        '''
        return np.linalg.norm(arr1-arr2)

    def Build_Tree(self,train_dataset_x):
        '''
        该函数为构造kd树，采用
        :param train_dataset_x: 训练集
        :return:返回空，但该函数实现了对类中kd树对象的构造
        '''
        charac_seq = kd_seq(train_dataset_x)
        ## charac_seq为选取特征的顺序
        k = len(train_dataset_x[0])  ##特征数
        ## charac_dim = level % k
        split_instance, left_instance, right_instance = kd_median(train_dataset_x[:, charac_seq[0]])
        root = kd_tree(split_instance=split_instance, charac_dim=charac_seq[0],
                       level=0, left_instance=left_instance, right_instance=right_instance)
        ##通过层序遍历构造出kd树
        queue = Queue()
        queue.put(root)  ##根节点入栈
        while queue.qsize() > 0:  # 队列不为空
            current_node = queue.get()
            father_level = current_node.level
            child_charac_seq = (father_level + 1) % k  ##该层对应的特征维度
            if (len(current_node.left_instance) > 0):
                split_instance, left_instance, right_instance = (kd_median(train_dataset_x[
                                                                               [current_node.left_instance], [
                                                                                   charac_seq[
                                                                                       child_charac_seq]] * len(
                                                                                   current_node.left_instance)][0]))
                ##split_instance:中位数样本索引
                ##left_instance:左划分索引
                ##right_instance:右划分索引
                ##下面这行代码的意思是:由于除根节点外，剩余kd树中结点对应的空间中的点均有可能不是全部的样本点，需要返回正确的索引。
                split_instance, left_instance, right_instance = current_node.left_instance[split_instance], \\
                                                                current_node.left_instance[left_instance], \\
                                                                current_node.left_instance[right_instance]
                ##构造左子树
                current_node.left_child = kd_tree(split_instance=split_instance, charac_dim=charac_seq[child_charac_seq],
                                                  level=father_level + 1,
                                                  left_instance=left_instance, right_instance=right_instance)
                queue.put(current_node.left_child)
            if (len(current_node.right_instance) > 0):
                split_instance, left_instance, right_instance = (kd_median(train_dataset_x[
                                                                               [current_node.right_instance], [
                                                                                   charac_seq[
                                                                                       child_charac_seq]] * len(
                                                                                   current_node.right_instance)][
                                                                               0]))
                ##返回原数组下标
                split_instance, left_instance, right_instance = current_node.right_instance[split_instance], \\
                                                                current_node.right_instance[left_instance], \\
                                                                current_node.right_instance[right_instance]
                current_node.right_child = kd_tree(split_instance=split_instance, charac_dim=charac_seq[child_charac_seq],
                                                   level=father_level + 1,
                                                   left_instance=left_instance, right_instance=right_instance)
                queue.put(current_node.right_child)
        self.kd_tree = root
        return


    def search(self,train_dataset_x,kd_tree,new_sample):
        ##在kd树中找出包含目标点x的叶节点：从指定结点kd_tree出发，可尝试非递归地向下访问kd树。
        ##注：kd_tree可以是根节点，也可以不是根节点。
        if kd_tree is None or kd_tree.has_visited is True:
            #if(kd_tree is None):
                # print("另一半区域为空。")
            #else:
                #print("另一半区域已经回溯过了。")
            return
        else:
            ## 向下访问kd树，并记录路径
            tmp = kd_tree
            while (tmp is not None):
                charac_dim = tmp.charac_dim
                ##若目标点x当前维的坐标大于切分点的坐标，则移动到右节点。
                if(new_sample[charac_dim] >= train_dataset_x[tmp.split_instance][charac_dim]):
                    self.route.append(tmp)
                    tmp = tmp.right_child
                else:
                    self.route.append(tmp)
                    tmp = tmp.left_child

                if(tmp is None):

                    if(self.route[-1].left_child is not None):
                        tmp = self.route[-1].left_child

                    elif(self.route[-1].right_child is not None):
                        tmp = self.route[-1].right_child

            if (self.lp_dis(train_dataset_x[self.route[-1].split_instance], new_sample) < self.low_dist):
                self.segmentation_sample = self.route[-1].split_instance
                self.low_dist = self.lp_dis(train_dataset_x[self.segmentation_sample], new_sample)
            self.has_calculate = np.concatenate((self.has_calculate,[train_dataset_x[self.route[-1].split_instance]]),axis=0)
            return

    def show_route(self):
        if(len(self.route) == 0):
            print("Route Empty!\\n")
        else:
            for i in self.route:
                if(i is None):
                    print("None"," ",end="")
                else:
                    print(i.split_instance," ",end="")
            print("\\n")


    def tracking(self,new_sample):
        while True:
            pre = self.route.pop()
            pre.has_visited = True
            if (len(self.route) == 0):
                break
            cur = self.route[-1]
            ## a.如果该结点保存的实例点比当前的最近点距离目标更近，则以该实例点为“当前最近点”。
            self.has_calculate = np.concatenate((self.has_calculate, [train_dataset_x[cur.split_instance]]),axis=0)
            if (self.lp_dis(train_dataset_x[cur.split_instance], new_sample) < self.low_dist):
                self.segmentation_sample = cur.split_instance
                self.low_dist = self.lp_dis(train_dataset_x[cur.split_instance], new_sample)

            another_area = cur.left_child if (pre == cur.right_child) else cur.right_child
            ##父节点分割的另一半是否存在更近的点？
            ## b.当前最近点一定存在于该结点一个子节点对应的区域。检查该子节点的父节点的另一子节点对应的区域是否有更近的点。
            ## 判断超球面是否能与超平面相交
            ## 以目标点为球心，以目标点与“当前最近点”间的距离为半径的超球体
            ## 半径:radius
            radius = self.low_dist
            ## 超球面球心到超平面的距离:dis
            dis = abs(new_sample[cur.charac_dim] - train_dataset_x[cur.split_instance][cur.charac_dim])
            if (radius > dis):
                # print("超球面与超平面相交,看另一半区域\\n")
                self.search(train_dataset_x,another_area,new_sample)
            else:
                # print("不相交\\n")
                continue


    def back_tracking(self,new_sample):
        ##预测样本输入维度和训练集不一致
        if(new_sample.size != train_dataset_x[0].size):
            print("Improper input!\\n")
        else:
            self.search(train_dataset_x, self.kd_tree, new_sample)
            self.tracking(new_sample=new_sample)
            print("kd树求出的最邻近点为", self.segmentation_sample, "号样本点",train_dataset_x[self.segmentation_sample]," ")
            print("对应kd树求出的最短距离为", self.low_dist, "\\n")
            return


k = k_neighbour()
test_data = np.array([30,50,70])
k.has_calculate = [test_data]
k.Build_Tree(train_dataset_x=train_dataset_x)
k.back_tracking(new_sample=test_data)
true_low_dist = float("inf")
index = -1
for i in range(len(train_dataset_x)):
    if(k.lp_dis(train_dataset_x[i],test_data)<true_low_dist):
        true_low_dist = k.lp_dis(train_dataset_x[i],test_data)
        index = i
print("真实结果样本为: ",index,"号样本点",train_dataset_x[index])
print("真实的最短距离为: ",true_low_dist,"\\n")
## 以下代码仅当特征空间为二维时可用。若特征空间不是二维，请删除以下代码。
# fig, ax = plt.subplots()
# ax.scatter(train_dataset_x[:,0],
#            train_dataset_x[:,1],
#            c = "blue",label="sample_point")
# ax.scatter(k.has_calculate[:,0],k.has_calculate[:,1],label="has_calculate",c = "orange",alpha = 1)
# ax.scatter(test_data[0],test_data[1],c = "red",label="target_sample",alpha = 1)
# ax.scatter(train_dataset_x[k.segmentation_sample][0],train_dataset_x[k.segmentation_sample][1],c = "green",label = "nearest",alpha = 1)
# box = ax.get_position()
# ax.set_position([box.x0, box.y0+0.05, box.width , box.height])
# ax.legend(loc='upper center', bbox_to_anchor=(0.5, -0.05),ncol=2)
# plt.show()

以上代码在特征空间中随机了10000个样本点，特征空间为三维
运行结果：

结果正确。

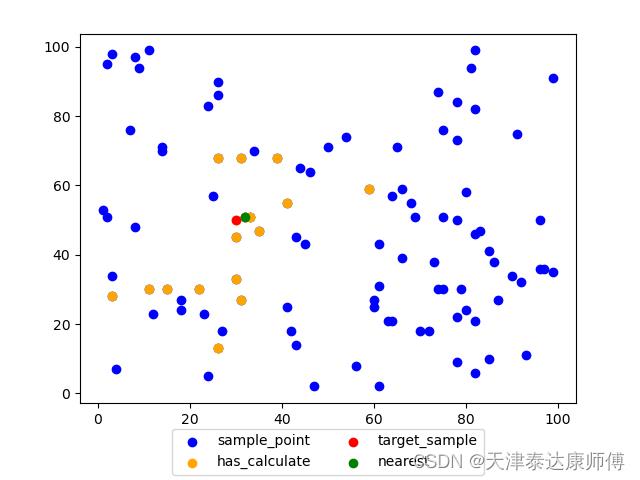
假设特征空间为二维，可直观展示
橙色点为搜索的结点
蓝色点为所有样本点
红色点为目标点
绿色点为最近邻点。