数据结构中哈夫曼树的应用（C语言）

Posted 2023-05-02

功能：
(1)从终端读入字符集大小n，以及n个字符和n个权值，建立哈夫曼树并将它存于文件hfmTree中.将已在内存中的哈夫曼树以直观的方式（比如树）显示在终端上；
(2)利用已经建好的哈夫曼树（如不在内存，则从文件htmTree中读入），对文件ToBeTran中的正文进行编码，然后将结果存入文件CodeFile中，并输出结果，将文件CodeFile以紧凑格式先是在终端上，每行50个代码。同时将此字符形式的编码文件写入文件CodePrint中。
(3)利用已建好的哈夫曼树将文件CodeFile中的代码进行译码，结果存入文件TextFile中，并输出结果。
分步实施：
1） 初步完成总体设计，搭好框架，确定人机对话的界面，确定函数个数；
2） 完成最低要求：完成功能1；
3） 进一步要求：完成功能2和3。有兴趣的同学可以自己扩充系统功能。
要求：1）界面友好，函数功能要划分好
2）总体设计应画一流程图
3）程序要加必要的注释
4） 要提供程序测试方案
5） 程序一定要经得起测试，宁可功能少一些，也要能运行起来，不能运行的程序是没有价值的。

#include<stdio.h>
#include<stdlib.h>
typedef int DataType;
#define MaxValue 10000
#define MaxBit 10
#define MaxN 100
#define N 100;
int n1=0;
char c[100];
typedef struct Node

DataType data;
struct Node *leftChild;
struct Node *rightChild;
BiTreeNode;
typedef struct

int weight;
int flag;
int parent;
int leftChild;
int rightChild;
HaffNode;

typedef struct

int bit[MaxN];
int start;
int weight;
Code;

struct worder

char words; /*字符*/
word[100];
struct weighted

int weighter; /*转换权值有利于文件的存储*/
weight[100] ;
void Initiate(BiTreeNode **root) /*初始化二叉树*/

*root=(BiTreeNode * )malloc(sizeof(BiTreeNode));
(*root)->leftChild=NULL;
(*root)->rightChild=NULL;

BiTreeNode *InsertLeftNode(BiTreeNode *curr,DataType x) /*插入左子树*/

BiTreeNode *s,*t;
if(curr==NULL) return NULL;
t=curr->leftChild;
s=(BiTreeNode *)malloc(sizeof(BiTreeNode));
s->data=x;
s->leftChild=t;
s->rightChild=NULL;
curr->leftChild=s;
return curr->leftChild;


BiTreeNode *InsertRightNode(BiTreeNode *curr ,DataType x) /*插入右子树*/

BiTreeNode *s,*t;
if(curr==NULL)
return NULL;
t=curr->rightChild;
s=(BiTreeNode *)malloc(sizeof(BiTreeNode));
s->data=x;
s->rightChild=t;
s->leftChild=NULL;
curr->rightChild=s;
return curr->rightChild;


void Haffman(int weigh[],int n,HaffNode haffTree[],int a[][3]) /*建立哈夫曼树*/

int i,j,m1,m2,x1,x2;

for(i=0;i<2*n-1;i++)


if(i<n)
haffTree[i].weight=weigh[i];
else haffTree[i].weight=0;
haffTree[i].parent=-1;
haffTree[i].flag=0;
haffTree[i].leftChild=-1;
haffTree[i].rightChild=-1;


for(i=0;i<n-1;i++)

m1=m2=MaxValue;
x1=x2=0;
for(j=0;j<n+i;j++)

if(haffTree[j].weight<m1&&haffTree[j].flag==0)

m2=m1;
x2=x1;
m1=haffTree[j].weight;
x1=j;

else if(haffTree[j].weight<m2&&haffTree[j].flag==0)

m2=haffTree[j].weight;
x2=j;


haffTree[x1].parent=n+i;
haffTree[x2].parent=n+i;
haffTree[x1].flag=1;
haffTree[x2].flag=1;
haffTree[n+i].weight=haffTree[x1].weight+haffTree[x2].weight;
haffTree[n+i].leftChild=x1;
haffTree[n+i].rightChild=x2;
a[i+1][0]=haffTree[x1].weight;
a[i+1][1]=haffTree[x2].weight; /*将每个权值赋值给二维数组a[][],利用这个二维数组可以进行建立二叉树*/
a[i+1][2]=haffTree[n+i].weight;



void HaffmanCode(HaffNode haffTree[],int n,Code haffCode[]) /*对已经建立好的哈夫曼树进行编码*/

Code *cd=(Code *)malloc(sizeof(Code));
int i,j,child,parent;

for(i=0;i<n;i++)

cd->start=n-1;
cd->weight=haffTree[i].weight;
child=i;
parent=haffTree[child].parent;
while(parent!=-1)

if(haffTree[parent].leftChild==child)
cd->bit[cd->start]=0;
else
cd->bit[cd->start]=1;
cd->start--;
child=parent;
parent=haffTree[child].parent;


for(j=cd->start+1;j<n;j++)
haffCode[i].bit[j]=cd->bit[j];
haffCode[i].start=cd->start+1;
haffCode[i].weight=cd->weight;



void PrintBiTree(BiTreeNode *bt ,int n) /*将哈夫曼树转换成的二叉树进行打印*/

int i;
if(bt==NULL)
return;
PrintBiTree(bt->rightChild,n+1);
for(i=0;i<n;i++)
printf(" ");
if(bt->data!=0&&bt->data<100)

if(n>0)

printf("---");
printf("%d\\n\\n",bt->data);


PrintBiTree(bt->leftChild,n+1);


int search(int a[][3],int m) /*查找和a[][2]相等的权值*/

int i=1;
if(m==1) return 0;
while(a[i][2]!=a[m][0]&&i<m)
i++;
if(i==m) return 0; /*查找失败返回数字0 查找成功返回和a[][2]相等的数的行数 i*/
else return i;


int searcher(int a[][3],int m) /*查找和a[][1]相等的权值*/

int i=1;
if(m==1) return 0;
while(a[i][2]!=a[m][1]&&i<m) /*查找失败返回数字0 查找成功返回和a[][1]相等的数的行数 i*/
i++;
if(i==m) return 0;
else return i;


void creat(BiTreeNode *p,int i,int a[][3]) /*建立哈夫曼树*/（利用递归）

int m,n;
BiTreeNode *p1,*p2,*p3;
if(i<=0) return;
p1=p;
if(a[i][0]!=a[i][1]) /*如果a[][0]和a[][1]不相等*/

p2=InsertLeftNode(p,a[i][0]); /*a[][0]为左子树*/
n=search(a,i);
if(n)
creat(p2,n,a);
p3=InsertRightNode(p1,a[i][1]); /*a[][1]为右子树*/
m=searcher(a,i);
if(m)
creat(p3,m,a);
/*如果a[][0]和a[][1]相等则只要进行一个的查找*/
else

p2=InsertLeftNode(p,a[i][1]);
n=searcher(a,i);
if(n)
creat(p2,n,a);
p3=InsertRightNode(p1,a[i][1]);



void code(Code myHaffCode[],int n ) /*编码*/

FILE *fp,*fp1,*fp2;
int i=0,k,j;
int text_len = strlen(c);
int *p2;
struct worder *p1;
if((fp2=fopen("CodeFile","wb"))==NULL) /*建立存储编码的文件*/

printf("Error,cannot open file\\n" );
exit(0);

if((fp1=fopen("hfmTree","rb"))==NULL) /*读取存储字符的文件*/

printf("\\n\\n Please,increase records first~!! \\n" );
return;

for(p1=word;p1<word+n;p1++)

fread(p1,sizeof(struct worder),1,fp1) ;
printf("word=%c Weight=%d Code=",p1->words,myHaffCode[i].weight); /*输出每个权值的编码*/
for(j=myHaffCode[i].start;j<n;j++)
printf("%d",myHaffCode[i].bit[j]);
printf("\\n");
printf("\\n");
i++;

j=0;
printf("\\n\\nThe codes :") ;
for(i=0;i< text_len;i++)

while(c[i]!=word[j].words) /*查找字符找到对应的编码*/

j++;

for(k=myHaffCode[j].start;k<n;k++)

printf("%d",myHaffCode[j].bit[k]); /*输出相应的编码*/
fprintf(fp2,"%d",myHaffCode[j].bit[k]);

j=0;


fclose(fp2);


void sava(int n) /*建立文件*/

FILE *fp,*fp1,*fp2;
int *p2,i,j;
struct worder *p1;
struct weighted *p3;
if((fp2=fopen("NO.","wb"))==NULL) /*建立存储权值个数的文件*/

printf("Error,cannot open file\\n" );
exit(0);

fprintf(fp2,"%d",n) ;
if((fp=fopen("hfmTree","wb"))==NULL) /*建立存储字符的文件*/

printf("Error,cannot open file\\n" );
exit(0);

for(p1=word;p1<word+n;p1++)

if(fwrite(p1,sizeof(struct worder),1,fp)!=1)
printf("file write error\\n");

fclose(fp);
if((fp1=fopen("hfmTree-1","wb"))==NULL) /*建立存储权值的文件*/

printf("Error,cannot open file\\n" );
exit(0);

for(p3=weight;p3<weight+n;p3++)

if(fwrite(p3,sizeof(struct weighted),1,fp1)!=1)
printf("file write error\\n");

fclose(fp1);
printf("Please input any key !\\n") ;

printf("Please input any key !\\n") ;
if(n>MaxN)

printf("error!\\n\\n");
exit(0);



void menu() /*界面*/


printf("\\n\\n\\n\\t\\t*************************************\\n\\n");
printf("\\t\\t\\t1. To Code:\\n\\n"); /*编码*/
printf("\\t\\t\\t2. Decoding:\\n\\n"); /*译码*/
printf("\\t\\t\\t3. Output the huffman Tree:\\n\\n"); /*打印哈夫曼树*/
printf("\\t\\t\\t4. New data\\n\\n");
printf("\\t\\t\\t5. Quit up...\\n\\n");
printf("\\n\\t\\t************************************\\n\\n");
printf("Input you choice :\\n");


void main()
FILE *fp,*fp1,*fp2,*fp3,*fp4;
int i,j;
int b[100][3],m=100,n,w,k=0,weigh[100];
struct worder *d;
struct weighted *p2;
char h;
BiTreeNode *root,*p;

HaffNode *myHaffTree=(HaffNode *)malloc(sizeof(HaffNode)*(2*m+1));
Code *myHaffCode=(Code *)malloc(sizeof(Code)*m);
Initiate(root);
if(((fp1=fopen("hfmTree","rb"))==NULL)&&((fp=fopen("hfmTree-1","rb"))==NULL))

loop:
printf("how many number do you want input?\\n");
scanf("%d",&n);
if((fp=fopen("hfmTree-1","wb"))==NULL)

printf("Error,cannot open file\\n" );
exit(0);

for(i=0;i<n;i++)

printf("\\nword[%d]=",i) ;
scanf("%s",&word[i].words) ;
printf("\\nweight[%d]=",i);
scanf("%d",&weight[i].weighter);

sava(n) ;

else

if((fp3=fopen("NO.","rb"))==NULL)

printf("\\n\\n Please,increase records first~!! \\n" );
return;

fscanf(fp3,"%d",&n);
if((fp=fopen("hfmTree-1","rb"))==NULL)

printf("\\n\\n Please,increase records first~!! \\n" );
return;

for(p2=weight;p2<weight+n;p2++)

fread(p2,sizeof(struct weighted),1,fp) ;
weigh[k]=p2->weighter ;
k++;

Haffman(weigh,n,myHaffTree,b);
HaffmanCode(myHaffTree,n,myHaffCode);
while(1)

do

clrscr();
menu();
scanf("%d",&w);
while(w!=1&&w!=2&&w!=3&&w!=4&&w!=5);
switch(w)

case 1: clrscr();
printf("plesase input :\\n");
scanf("%s",&c) ;
if((fp2=fopen("ToBeTran","wb"))==NULL)

printf("Error,cannot open file\\n" );
exit(0);

fprintf(fp2,"%s",c) ;
fclose (fp2);
code(myHaffCode,n) ;
getch();
break;
case 2: if((fp2=fopen("ToBeTran","rb"))==NULL)

printf("\\n\\n Please,increase records first~!! \\n" );
return;

fscanf(fp2,"%s",&c);
printf("The words:");
printf("%s",c);
if((fp4=fopen("TextFile.","wb"))==NULL)

printf("Error,cannot open file\\n" );
exit(0);

fprintf(fp4,"%s",c) ;
fclose (fp4);
getch();
break;
case 3: clrscr();
printf("The huffman Tree:\\n\\n\\n\\n\\n\\n");
p=InsertLeftNode(root,b[n-1][2]);
creat(p,n-1,b);
PrintBiTree(root->leftChild,n);
printf("\\n");
getch();
clrscr();
break;
case 4:goto loop;

case 5:exit(0);



getch();
参考技术A /* 哈夫曼编码*/
#include "graphics.h"
#include "stdlib.h"
#include "Stdio.h"
#include "Conio.h"
#define MAX 53

char bmfile[10];
char a[100];
typedef struct
char c,s[10];MM;
MM mm[53];

typedef struct /*以数组存储哈夫曼树时的结点类型*/
char ch;
int w,lcd,rcd,pt; /*权值、左孩子、右孩子、双亲*/
HuffNode;
HuffNode Hm[MAX];

typedef struct CNode /*Auffman编码的结点类型*/
char c;
struct CNode *prv;
CODE;
CODE *cd;

wjbm1 (char a[])/*从文件中读取要进行编码的字符*/
FILE *fp3;
char ch;
int i=0,n=0,k,t,m;
/*printf("\n输入要编码的文件名：");
scanf("%s",bmfile);*/
if((fp3=fopen("bmfile.txt","r"))==NULL)
printf("\n文件不存在");
exit(0);

while(!feof(fp3))
a[i++]=fgetc(fp3);
a[i]='\0';
for(i=0;a[i]!='\0';i++)
if(a[i]>='A'&&a[i]<='Z') Hm[a[i]-65].ch=a[i]; Hm[a[i]-65].w++;
if(a[i]>='a'&&a[i]<='z') Hm[a[i]-71].ch=a[i]; Hm[a[i]-71].w++;
if(a[i]==' ') Hm[52].ch=' ';Hm[52].w++;

for(i=0;i<53;i++)
if(Hm[i].w!=0)
Hm[n].ch=Hm[i].ch;
Hm[n].w=Hm[i].w;
Hm[n].lcd=-1;
Hm[n].rcd=-1;
Hm[n].pt=-1;
n++;
fclose(fp3);
return n;


zfbm1(char a[])

int n=0,i;
gets(a);
for(i=0;a[i]!='\0';i++)
if(a[i]>='A'&&a[i]<='Z') Hm[a[i]-65].ch=a[i]; Hm[a[i]-65].w++;
if(a[i]>='a'&&a[i]<='z') Hm[a[i]-71].ch=a[i]; Hm[a[i]-71].w++;
if(a[i]==' ') Hm[52].ch=' ';Hm[52].w++;

printf("\n叶字信息(字符、权值):");
for(i=0;i<53;i++)
if(Hm[i].w!=0)
printf("(%c,%d)",Hm[i].ch,Hm[i].w);
Hm[n].ch=Hm[i].ch;
Hm[n].w=Hm[i].w;
Hm[n].lcd=-1;
Hm[n].rcd=-1;
Hm[n].pt=-1;
n++;
return n;


charTJ()
char c;
int i;
printf("\n1-从文件中读取字符生成树;2-从键输入字母生成树;3-退出;\n");
while(1)
switch(c=getch())
case '1':wjbm1(a);return;
case '2':puts("\n输入字母");zfbm1(a);return;
case '3':return;
default:printf("\n输入无效,重新输入");scanf("%d",&c);


void HuffmanCode(int n) /*哈夫曼编码。n为哈夫曼树的叶子数*/
int i,k,t;
CODE *p,*h;

cd=(CODE*)malloc(sizeof(CODE)*n);/*用于存储每个叶子的编码(链栈)*/
for(i=0;i<n;i++) /*搜索第i+1个叶子*/
k=i;h=0;
while((Hm+k)->pt>=0)
if((Hm+(Hm+k)->pt)->lcd==k)t=0;else t=1;
p=(CODE*)malloc(sizeof(CODE));
p->c=48+t;p->prv=h;h=p;
k=(Hm+k)->pt;

cd[i].prv=h;



void dispCodes(int n) /*显示*/
int i,j=0;
CODE *p;
for(i=0;i<n;i++)
p=cd[i].prv;
/*printf("\n%c:",Hm[i].ch); */
mm[i].c=Hm[i].ch;
j=0;
while(p)
/*printf("%c",p->c);*/ mm[i].s[j++]=p->c;
mm[i].s[j]='\0';
p=p->prv;


puts("\n显示结果：");
for(i=0;i<n;i++)
printf("(%c,%s) ",mm[i].c,mm[i].s);
dispCode(n);


dispCode(int n) /*将各字符的编码存入数组mm*/
int i,j;
CODE *p;
for(i=0;i<n;i++)
p=cd[i].prv;
/*printf("\n%c:",Hm[i].ch); */
mm[i].c=Hm[i].ch;
j=0;
while(p)
/*printf("%c",p->c);*/ mm[i].s[j++]=p->c;
mm[i].s[j]='\0';
p=p->prv;




Huffmanshu(int n) /*显示哈夫曼树的字符编码*/
int i;
HuffmanCode(n);
dispCodes(n);


wjbm(int n)
FILE *fp4;
char ch;
int i=0,j;
wjbm1(a);
HuffmanCode(n);
dispCode(n);
fp4=fopen("stfile.txt","w");
for(i=0;a[i]!='\0';i++)
for(j=0;j<n;j++)
if(a[i]==mm[j].c) fputs(mm[j].s,fp4);

puts("结果已写入文件");
fclose(fp4);


zfbm(int n)
int i,j;
puts(a);
HuffmanCode(n);
dispCode(n);
printf("译码:");
for(i=0;a[i]!='\0';i++)
for(j=0;j<n;j++)
if(a[i]==mm[j].c) printf("%s",mm[j].s);


Huffmanbm(int n,HuffNode Hm[])/*哈夫曼编码*/

int k;
char ch;
printf("\n1-结果输出到文件；2-结果显示在屏幕;3-退出;\n");
while(1)
switch(ch=getch())
case '1':wjbm(n);return 0;
case '2':printf("\n源码:");zfbm(n);return;
case '3':return 0;
default:printf("输入无效,重新输入");scanf("%d",&ch);


wjjm(int n,char a[])
FILE *fp1,*fp2;
char ch;
int i=0,k,t,m;
if((fp1=fopen("jmfile.txt","r"))==NULL)
printf("\n文件不存在");
exit(0);
fp2=fopen("st.txt","w");
while(!feof(fp1)) a[i++]=fgetc(fp1);
a[i]='\0'; k=i;
printf("\n1-结果输出到文件；2-结果显示在屏幕;3-退出;\n");
t=2*n-2;

while(1)
switch(ch=getch())
case '1':
for(i=0;i<=k;)
if(a[i]=='0')
if(Hm[t].lcd==-1) putc(Hm[t].c,fp2); t=2*n-2;else t=Hm[t].lcd;i++;
else
if(Hm[t].rcd==-1) fputc(Hm[t].c,fp2); t=2*n-2;else t=Hm[t].rcd;i++;
return;
case'2':
for(i=0;i<=k;)
if(a[i]=='0')
if(Hm[t].lcd==-1) printf("%c",Hm[t].c); t=2*n-2;else t=Hm[t].lcd;i++;
else
if(Hm[t].rcd==-1) printf("%c",Hm[t].c); t=2*n-2;else t=Hm[t].rcd;i++;
return;
case'3':return 0;


fclose(fp1);
fclose(fp2);


zfjm(int n,char a[])/*对输入的字符进行解码*/
int i,t,k;
printf("\n输入要解码的信息:");
scanf("%s",a);
k=strlen(a);
t=2*n-2;
printf("生成源代码：");
for(i=0;i<=k;)
if(a[i]=='0')
if(Hm[t].lcd==-1) printf("%c",Hm[t].c); t=2*n-2;else t=Hm[t].lcd;i++;
else
if(Hm[t].rcd==-1) printf("%c",Hm[t].c); t=2*n-2;else t=Hm[t].rcd;i++;


void Huffmanjm(int n,HuffNode Hm[]) /*哈夫曼解码。n为哈夫曼树的叶子数*/
int m=n;
char *a,ch;
printf("\n1-对文件解码；2-对字符解码;3-退出;\n");
while(1)
switch(ch=getch())
case '1':wjjm(m,a);return 0;
case '2':zfjm(m,a);return;
case '3':return 0;



void HuffmanTree() /*生成哈夫曼树*/
int i,j,x,y,n;
char c;
n=charTJ();
for(i=0;i<n-1;i++)
x=0;
while((Hm+x)->pt>=0)x++; /*搜索第一个未处理的结点*/
y=x+1;
while((Hm+y)->pt>=0)y++; /*搜索第二个未处理的结点*/
j=y;
if((Hm+x)->w>(Hm+y)->w)j=y;y=x;x=j;
for(j=j+1;j<n+i;j++) /*搜索两个未处理且权值最小的结点*/
if((Hm+j)->pt<0&&(Hm+j)->w<(Hm+x)->w) y=x;x=j;
else
if((Hm+j)->pt<0&&(Hm+j)->w<(Hm+y)->w) y=j;

(Hm+x)->pt=n+i;(Hm+y)->pt=n+i;(Hm+n+i)->w=(Hm+x)->w+(Hm+y)->w;
(Hm+n+i)->lcd=x;(Hm+n+i)->rcd=y;(Hm+n+i)->pt=-1;

puts("\n1-显示字符的编码;2-编码;3-解码;4-退出;");
while(1)
switch(c=getch())
case '1':Huffmanshu(n);break;
case '2':Huffmanbm(n,Hm);break;
case '3':Huffmanjm(n,Hm);break;
case '4':return;




int main()
char c;
gotoxy(29,1);
puts("文件编码解码系统");
window(1,3,80,25);
HuffmanTree();
getch();
clrscr();

王道数据结构5.2（树的应用）

树的应用

• 一、二叉排序树
• • (一) 基础
  • (二) 操作
  • • 1. 二叉排序树的查找
    • 2. 二叉排序树的插入
    • 3. 二叉排序树的构造
    • 4. 二叉排序树的删除
    • 5. 查找效率分析
• 二、平衡二叉树
• • （一）定义
  • （二）操作
  • • 1. 二叉平衡树的插入
• 三、哈夫曼树
• • 1. 带权路径长度
  • 2.哈夫曼树的构造
  • 3. 哈夫曼编码

一、二叉排序树

(一) 基础

1. 定义：又称为二叉查找树，一棵二叉树或空二叉树，或者具有如下性质的二叉树：
   ① 左子树上所有结点的关键字均小于根结点的关键字。
   ② 右子树上所有结点的关键字均大于根结点的关键字。
   ③ 左右子树又各是一棵二叉排序树。
2. 利用中序遍历，可以得到一个递增的有序序列。

(二) 操作

1. 二叉排序树的查找

（1）思想：
若树非空，目标值与根结点的值比较：
①若相等，则查找成功。
②若小于根结点，则查找左子树，若大于根结点，则查找右子树
查找成功则返回节点指针，查找失败，则返回NULL。
（2）代码：

//二叉排序树结点 
typedef struct BSTNode
    int key;
    struct BSTNode *lchild,*rchild;
BSTNode,*BSTree;
//在二叉排序树中查找值为key的结点（非递归）
BSTNode *BST_Search(BSTNode T,int key)
   while(T!=NULL&&key!=T->key)
        if(key<T->key)
           T=T->lchild;
        else T=T->rchild;
   
   return T;

//在二叉排序树中查找值为key的结点（递归）
BSTNode *BSTSearch(BSTree T,int key)
    if(T==NULL)
        returm NULL;
    if(key==T->key)
        return T;
    else if(key==T->key)
        return BSTSearch(T->lchild,key)；
    else
        return BSTSearch(T->rchild,key);

3. 分析：
   ① 非递归算法时间复杂度为O(1)
   ② 最坏时间复杂度为O(h)

2. 二叉排序树的插入

1. 思想：若原二叉排序树为空，则直接插入结点，否则，若关键字k小于根结点值，则插入左子树，若关键字k大于根结点，则插入到右子树。
2. 代码：

//在二叉排序树插入关键字k的新结点（递归实现）
int BST_Insert(BSTree &T,int k)
  if(T==NULL)
     T=(BSTree)malloc(sizeof(BSTNode));
    T->key=k;
    T->lchild=T->rchild=NULL;
    return 1;
  
  else if(k==T->key)
    return 0;
  else if(k<T->key)
    return BST_Insert(T->lchild,k);
  else 
    return BST_Insert(T->rchild,k);

3. 二叉排序树的构造

1. 代码：

//按照str[]中的关键字序列建立二叉排序树
void Creat_BST(BSTree &T,int str[],int n)
  T=NULL;
  int i=0;
  while(i<n)
    BST_Insert(T,str[i]);
    i++;
  

//插入结点
int BST_Insert(BSTree &T,int k)
  if(T==NULL)
     T=(BSTree)malloc(sizeof(BSTNode));
    T->key=k;
    T->lchild=T->rchild=NULL;
    return 1;
  
  else if(k==T->key)
    return 0;
  else if(k<T->key)
    return BST_Insert(T->lchild,k);
  else 
    return BST_Insert(T->rchild,k);

2. 分析：
   不同的str[]序列可能得到同款二叉排序树，也可能得到不同的二叉排序树。
3. 实例
   

4. 二叉排序树的删除

1. 思想：
   （1） 先搜索找到目标节点：
   ① 如果被删除节点是叶子结点，则直接删除，不会破坏二叉排序树的性质
   ② 若z结点只有一棵左子树或右子树，则让z的子树成为z父节点的子树，代替z的位置。
   ③ 若z结点存在左右子树，则令z的直接后继（或直接前驱）代替z，然后从二叉排序树中山区这个直接后继（或直接前驱），这样就转换成了①或②情况。【z的后继：z的右子树中最左下结点，该结点一定没有左子树；z的前驱：z的左子树中最右下结点，该结点一定没有右子树】
   

5. 查找效率分析

1. 查找长度—在查找算法中，需要对比关键字的次数称为查找长度，反映了查找操作时间复杂度。
2. 若树高h，为了找到最下层的结点需要对比h次。
3. 最好情况：n个结点的二叉树最小高度为log2n+1【向下取整】
4. 最坏情况：每个结点只有一个分支，树高h=节点数n，平均查找长度=O(n)
5. 实例
   ① 查找成功的平均查找时间
   
   查找失败的平均查找长度ASL
   

二、平衡二叉树

（一）定义

1. 简称平衡树（AVL树）—书上任意结点的左子树和右子树的高度之差不超过1。【G.M.Adelson-Velsky和E.M.Landis】
2. 结点的平衡因子=左子树高-右子树高。
3. 平衡二叉树结点的平衡因子的值只可能是-1,0或1。只要有任意一点平衡因子绝对值大于1，则不是平衡二叉树。
4. 构造结构

//二叉排序树结点 
typedef struct AVLNode
    int key;
    int balance;//平衡因子
    struct AVLNode *lchild,*rchild;
AVLNode,*AVLTree;

（二）操作

1. 二叉平衡树的插入

（1）最小不平衡子树：从插入点往回找到第一个不平衡节点，调整以该结点的根的子树。
（2）插入后查找路径上的所有结点的平衡因子都会发生变化。
（3）寻找最小不平衡子树

（4）只需要将最小不平衡子树调整平衡，其他祖先结点都会恢复平衡。
（5）调整不平衡子树
① LL（在A的左孩子的左子树中插入导致不平衡）
右单旋转：由于在结点A的左孩子的左子树上插入了新结点，A的平衡因子从1增至2，导致以A上为根的子树失去平衡，需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根结点，将A结点向右下旋转成为B的右子树的根结点，而B的原右子树则作为A结点的左子树。

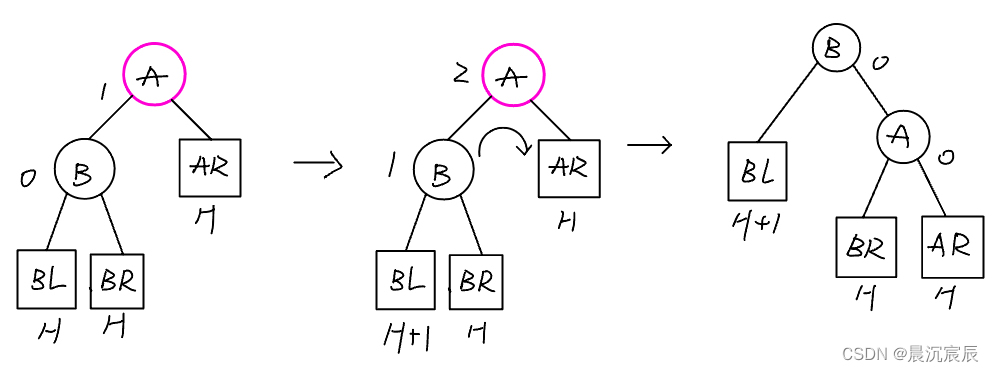
②RR（在A的右孩子的右子树中插入导致不平衡）
左单旋转：由于在结点A的右孩子的右子树上插入了新结点，A的平衡因子从-1增至-2，导致以A上为根的子树失去平衡，需要一次向左的旋转操作。将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，而B的原左子树则作为A结点的右子树。

③ LR（在A的左孩子的右子树中插入导致不平衡）
先左旋后右旋：由于在A的左孩子L的右子树R上插入新结点，A的平衡因子由1增至2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先左旋后右旋。先将A结点的左孩子B的右子树的根结点C向左上旋转提升到B结点的位置，然后再把该C结点向右上旋转提升到A结点的位置。

④ RL（在A的右孩子的左子树中插入导致不平衡）
先右后左旋转
由于在A的右孩子L的左子树R上插入新结点，A的平衡因子由-1增至-2，导致以A为根的子树失去平衡，需要进行两次旋转操作，先右旋后左旋。先将A结点的右孩子B的左子树的根结点C向右上旋转提升到B结点的位置，然后再把该C结点向左上旋转提升到A结点的位置。
（6）代码

• 实现f向右下旋转，p向右上旋转：其中f是父节点，p为左孩子，gf为f的父节点

  f->lchild=p->rchild;
    p->rchild=f;
    gf->lchild/rchild = p;

• 实现f向左下旋转，p向左上旋转：其中f是父节点，p为右孩子，gf为f的父节点

  f->rchild=p->lchild;
    p->lchild=f;
    gf->lchild/rchild = p;

2. 查找效率分析
   （1）若树高为h，则最坏情况下，查找一个关键字最多需要对比h次，即查找操作的时间复杂度不可能超过O(h)。
   （2）平衡二叉树——树上任意结点的左子树和右子树的高度之差不超过1。
   （3）假设以nh表示深度为h的平衡树中含有最少节点数。则有n0=0，n1=1，n2=2，并且有nh=nh-1+nh-2+1。【n3=4，n4=7，n5=12，n=9，则说明高最大为4】
   可以证明含有n个结点的平衡二叉树的最大深度为O(log2n)，平衡二叉树的平均查找长度为O(log2n)。

三、哈夫曼树

1. 带权路径长度

（1）结点的权：有某种现实含有的数值（如：表示结点的重要性等）
（2）结点的带权路径长度：从树的根到该结点的路径长度（经过的边数）与该结点上权值的乘积。
（3）树的带权路径长度：树中所有叶结点的带权路径长度之和wpl
（4）在含有n个带权也结点的二叉树中，其中带权路径长度最小的二叉树称为哈夫曼树，也称最优二叉树。

2.哈夫曼树的构造

（1）给定n个权值分别为w1, w2,…, wn的结点，构造哈夫曼树的算法描述如下：
1）将这n个结点分别作为n棵仅含一个结点的二叉树，构成森林F。
2）构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新
结点的权值置为左、右子树上根结点的权值之和。
3）从F中删除刚才选出的两棵树，同时将新得到的树加入F中。
4）重复步骤2）和3），直至F中只剩下一棵树为止。

（2）规律：

• 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大
• 哈夫曼树的结点总数为2n − 1
• 哈夫曼树中不存在度为1的结点。
• 哈夫曼树并不唯一，但WPL必然相同且为最优

3. 哈夫曼编码

100个选择题的答案
（1）固定长度编码——每个字符用相等长度的二进制位表

• ASCII编码
  A——0100 0001
  B——0100 0010
  C——0100 0011
  D——0100 0100
  8*100=800
• 每个字符用长度为2的二进制表示
  假设，100题中有80题选C，10题选A，8题选B，2题选D
  所有答案的二进制长度=802+102+82+22=200 bit
  （2）可变长度编码——允许对不同字符用不等长的二进制位表示
  若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码
  
  （3）有哈夫曼树得到哈夫曼编码——字符集中的每个字符作为一个叶子结点，各个字符出现的频度作为结点的权值，根据之前介绍的方法构造哈夫曼树.
  （4）注意：
  ① 哈夫曼树不唯一，因此哈夫曼编码不唯一。
  ② 哈夫曼编码可用于数据压缩。