数学建模—— 人口增长模型的确定
Posted 大彤小忆
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数学建模—— 人口增长模型的确定相关的知识,希望对你有一定的参考价值。
一、题目要求
1790-1980年间美国每隔10年的人口数量记录如下表所示。
| 年份 | 1790 | 1800 | 1810 | 1820 | 1830 | 1840 | 1850 | 1860 | 1870 | 1880 | 1890 | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 | 1960 | 1970 | 1980 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 人口 ( × 1 0 6 ) \\left (\\times 10^6 \\right ) (×106) | 3.9 | 5.3 | 7.2 | 9.6 | 12.9 | 17.1 | 23.2 | 31.4 | 38.6 | 50.2 | 62.9 | 76.0 | 92.0 | 106.5 | 123.2 | 131.7 | 150.7 | 179.3 | 204.0 | 226.5 |
- 1.试用以上数据建立马尔萨斯(Malthus)人口指数增长模型,对接下来的每隔十年预测五次人口数量,并查阅实际数据进行比对分析。
- 2.如果数据不相符,再对以上模型进行改进,寻找更为合适的模型进行预测,并对两次预测结果进行对比分析。
二、相关的基础知识
关于人口增长的模型常用的有马尔萨斯人口指数增长模型、Logistic增长模型以及改进的Logistic模型,它们常被用于预测人口增长。本次问题求解中除了使用这三种常用的人口增长模型外,还使用了BP神经网络模型来预测人口。
2.1 马尔萨斯(Malthus)人口指数增长模型
提出: 马尔萨斯模型来自于英国经济学家托马斯·罗伯特·马尔萨斯于1798年发表的《人口原理》。
马尔萨斯的人口论指出: 在没有生存资源限制的情况下,人口或生物种群的数量成指数增长。
定义: 关于人口或种群增长的模型。
模型的建立: 人口数量在单位时间内增长的百分比
r
r
r 是一定的,写成一个微分方程的形式,设
t
=
0
t = 0
t=0时刻的人口数量为
N
0
N_0
N0,则
t
t
t 时刻的总人口
N
t
N_t
Nt满足
1
N
t
d
N
t
d
t
=
r
⇒
N
t
=
N
0
e
r
t
\\frac1N_t\\fracdN_tdt=r\\Rightarrow N_t=N_0e^rt
Nt1dtdNt=r⇒Nt=N0ert
马尔萨斯认为,如果人口长期不受控制的话,指数增长的速度会十分惊人,生存资源的增长速度将无法满足众多人口的生存需要,从而产生一系列人口问题,严重时甚至会爆发饥荒、战争和疾病来除去资源与环境无法承受的过剩人口。
2.2 逻辑斯蒂(Logistic)增长模型
马尔萨斯人口论自提出以来,就一直是一个备受争议的理论。例如:在受到资源环境限制的情况下,人口还能否做指数爆炸式的增长呢?假设资源环境能承受的人口数量为 K K K,则可以建立一个Logistic方程 1 N t d N t d t = r ( 1 − N t K ) \\frac1N_t\\fracdN_tdt=r\\left (1-\\fracN_tK \\right ) Nt1dtdNt=r(1−KNt)
这个方程将得出仅在人口
N
t
<
<
K
N_t<<K
Nt<<K 时,
N
t
=
N
0
e
r
t
N_t=N_0e^rt
Nt=N0ert才是指数增长的。当接近
K
K
K时,人口的增长明显受到天花板
K
K
K的压制。虽然
N
t
>
K
N_t> K
Nt>K时确实会出现人口的负增长,但不过是平稳地趋近于平衡水平
K
K
K,而并不会发生马尔萨斯所担心的灾难性人口锐减的行为。下图给出了
K
K
K 随时间缓慢线性增加时,人口从不同的初条件以不同的生育率
r
r
r 增长的数值模拟结果。最终人口都达到了跟随
K
K
K(灰线)的线性增加行为。
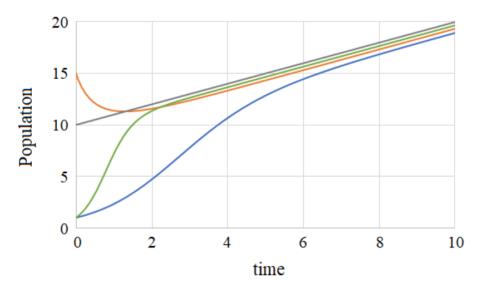 那么是不是可以说由于生存资源
K
K
K 的算术级增长,人口实际上并不能长期持续地指数增长,而是也会适应
K
K
K 变为算术级增长,所以马尔萨斯其实在杞人忧天地担心一个伪命题?
那么是不是可以说由于生存资源
K
K
K 的算术级增长,人口实际上并不能长期持续地指数增长,而是也会适应
K
K
K 变为算术级增长,所以马尔萨斯其实在杞人忧天地担心一个伪命题?
逻辑斯蒂方程( Logistic Equation)为马尔萨斯( Malthus) 人口模型的推广。
2.3 改进的Logistic模型
虽然Logistic模型考虑了环境容纳量,认为增长率是随着人口的增加而递减的,但Logistic模型中的增长率是线性递减的。事实上,随着人口的增加,人口基数越来越大,出生率也是增大的,导致增长率的减小是逐渐缓慢的。因此,增长率的逐年递减是非线性的。所以需要对Logistic模型进行改进,使得增长率的变化是非线性的。
2.4 BP神经网络模型
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络。
BP神经网络是一种多层前馈神经网络,该网络的主要特点是:信号前向传播、误差反向传播。在前向传播中,输入信号从输入层经隐含层逐层处理,直至输出层,每一层的神经元状态只影响下一层神经元状态。如果输出层得不到期望输出,则转入反向传播,根据预测误差调整网络权值和阈值,从而使BP神经网络输出不断逼近期望输出。
BP可以用于数据预测,在已知过去和当前的数据下,可以对未来数据进行估计。
三、模型的建立与求解
针对本次的题目使用了Malthus模型、Logistic模型、改进的Logistics模型、BP神经网络模型四种模型进行建模。
为了更清楚地反应各模型的预测准确度,令1790-2020年间预测人口数和实际人口数偏差之和为:
E
=
∑
t
=
0
24
∣
N
(
t
)
−
N
p
(
t
)
∣
E=\\sum_t=0^24 \\left | N(t)-N_p(t) \\right |
E=t=0∑24∣N(t)−Np(t)∣
其中, t = 0 , 1 , … , 24 t=0,1,…,24 t=0,1,…,24分别表示年份1790,1800,…,2020, N ( t ) N(t) N(t)和 N p ( t ) Np(t) Np(t)分别表示第 t t t个年份的实际人口和预测人口数量。
3.1 Malthus模型
- 模型的建立
在最简单的情况下,人口预测采用指数增长函数,建模的思路如下:假定 t 0 = 1790 t_0=1790 t0=1790年的人口数为 N 0 N_0 N0,人口增长率 r r r为常数,则第 t t t年的人口为 N ( t ) N\\left ( t \\right ) N(t)。其数学模型为: N ( t ) = N 0 e r ( t − t 0 ) = N 0 e r Δ t N ( 0 ) = N 0 \\left\\\\beginmatrix N\\left ( t \\right )=N_0e^r\\left ( t-t_0 \\right )=N_0e^r\\Delta t \\\\ N\\left ( 0 \\right )=N_0\\beginmatrix & & & & & & & \\endmatrix \\endmatrix\\right. N(t)=N0er(t−t0)=N0erΔtN(0)=N0 - 模型的求解
使用MATLAB的cftool工具箱对数据进行拟合:

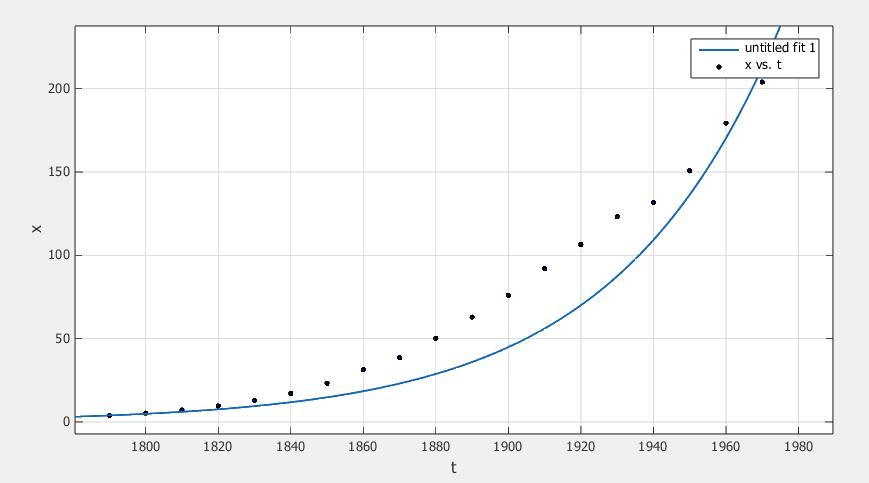
拟合得: r = 0.02222 r = 0.02222 r=0.02222
模型为: N ( t ) = 3.9 ∗ e x p ( 0.02222 ∗ ( t − 1790 ) ) N(t)= 3.9*exp(0.02222*(t-1790)) N(t)=3.9∗exp(0.02222∗(t−1790))
3.2 Logistic模型
- 模型的建立
马尔萨斯模型虽然在一定程度上反映了人口数量随着时间的推移的变化规律,但是根据马尔萨斯模型随着时间的推移人口成指数增长,这显然是不符合事实的。当人口数量较少时,自然资源比较丰富,人口增长相对较快,自然增长率可以在短期维持一个常数。但当人口达到一定水平后,受到自然资源相对稀缺的影响,人口增长率开始下降。设人口自然增长率 r ( t ) = r N ( t ) [ 1 − N ( t ) K ] r(t)=rN(t)\\left [ 1-\\fracN(t)K \\right] r(t)=rN(t)