Tensorflow学习笔记：神经网络优化
Posted 代表最低水平的hhhuster
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Tensorflow学习笔记：神经网络优化相关的知识，希望对你有一定的参考价值。
本文是个人的学习笔记，是跟随北大曹健老师的视频课学习的
附：bilibili课程链接 和 MOOC课程链接 以及 源码下载链接 （提取码：mocm）
文章目录
一、预备知识
1. 条件判断和选择（where）
a = tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
c = tf.where(tf.greater(a, b), a, b) # 条件?T/N
print('c:'.format(c))
结果
c:[1 2 3 4 5]
2. [0, 1)随机数（random.RandomState.rand）
rdm = np.random.RandomState()
a = rdm.rand() # scalar
b = rdm.rand(2, 3)
print('a=,\\n b='.format(a, b))
结果
a=0.7902641789078835,
b=[[0.25573684 0.43114347 0.05323669]
[0.93982238 0.01915588 0.99566242]]
3. 数组垂直叠加（vstack）
rdm = np.random.RandomState()
a = rdm.rand(3)
b = rdm.rand(3)
c = np.vstack((a, b))
print('a=, b=, \\nc='.format(a, b, c))
结果
a=[0.61471964 0.41927043 0.76723631], b=[0.44699221 0.00728193 0.60133098],
c=[[0.61471964 0.41927043 0.76723631]
[0.44699221 0.00728193 0.60133098]]
4. 网格生成（mgrid，ravel，c_）
x, y = np.mgrid[1:3, 2:4:0.5]
grid = np.c_[x.ravel(), y.ravel()]
print('x=,\\ny=,\\ngrid='.format(x, y, grid))
结果
x=[[1. 1. 1. 1.]
[2. 2. 2. 2.]],
y=[[2. 2.5 3. 3.5]
[2. 2.5 3. 3.5]],
grid=[[1. 2. ]
[1. 2.5]
[1. 3. ]
[1. 3.5]
[2. 2. ]
[2. 2.5]
[2. 3. ]
[2. 3.5]]
二、神经网络复杂度、学习率选取
1. 复杂度
空间：层数；时间：乘加运算次数。
2. 学习率更新
（1）影响
学习率过小 → \\rightarrow →更新过慢；学习率过大 → \\rightarrow →不收敛
（2）更新策略
这里老师推荐了指数衰减学习率
l
r
=
l
r
0
a
,
a
=
e
p
o
c
h
/
u
p
d
a
t
e
s
t
e
p
lr=lr_0^a, ~~~~~a=epoch/update~step
lr=lr0a, a=epoch/update step
代码实现
for epoch in range(epoches): # 每一次epoch遍历一次数据集
Loss = 0
lr = lr_base * lr_decay ** (epoch / lr_step)
for step, (x_train, y_train) in enumerate(data_train): # 每一个step遍历一个batch
...
print('After epoch, lr='.format(epoch, w1, lr))
结果
After 0 epoch, lr=0.2
After 1 epoch, lr=0.198
After 2 epoch, lr=0.19602
After 3 epoch, lr=0.1940598
After 4 epoch, lr=0.192119202
After 5 epoch, lr=0.19019800998
After 6 epoch, lr=0.1882960298802
After 7 epoch, lr=0.186413069581398
After 8 epoch, lr=0.18454893888558402
After 9 epoch, lr=0.18270344949672818
...
After 90 epoch, lr=0.08094639453566477
After 91 epoch, lr=0.08013693059030812
After 92 epoch, lr=0.07933556128440503
After 93 epoch, lr=0.07854220567156098
After 94 epoch, lr=0.07775678361484537
After 95 epoch, lr=0.07697921577869692
After 96 epoch, lr=0.07620942362090993
After 97 epoch, lr=0.07544732938470083
After 98 epoch, lr=0.07469285609085384
After 99 epoch, lr=0.07394592752994529
三、激活函数、损失函数
1. 几种激活函数介绍
(1) Sigmoid函数
y
=
σ
(
x
)
=
1
1
+
e
−
x
,
d
y
d
x
=
σ
′
(
x
)
=
y
(
1
−
y
)
y=\\sigma(x)=\\frac11+e^-x,~~~~\\fracdydx=\\sigma'(x)=y(1-y)
y=σ(x)=1+e−x1, dxdy=σ′(x)=y(1−y)
简证
σ
′
(
x
)
=
d
d
x
(
1
+
e
−
x
)
−
1
=
−
(
1
+
e
−
x
)
−
2
⋅
e
−
x
⋅
(
−
1
)
=
e
−
x
(
1
+
e
−
x
)
2
=
1
1
+
e
−
x
e
−
x
1
+
e
−
x
=
1
1
+
e
−
x
(
1
−
1
1
+
e
−
x
)
=
y
(
1
−
y
)
\\sigma'(x)=\\fracddx(1+e^-x)^-1=-(1+e^-x)^-2\\cdot e^-x\\cdot (-1)=\\frace^-x(1+e^-x)^2=\\frac11+e^-x\\frace^-x1+e^-x=\\frac11+e^-x(1-\\frac11+e^-x)=y(1-y)
σ′(x)=dxd(1+e−x)−1=−(1+e−x)−2⋅e−x⋅(−1)=(1+e−x)2e−x=1+e−x11+e−xe−x=1+e−x1(1−1+e−x1)=y(1−y)
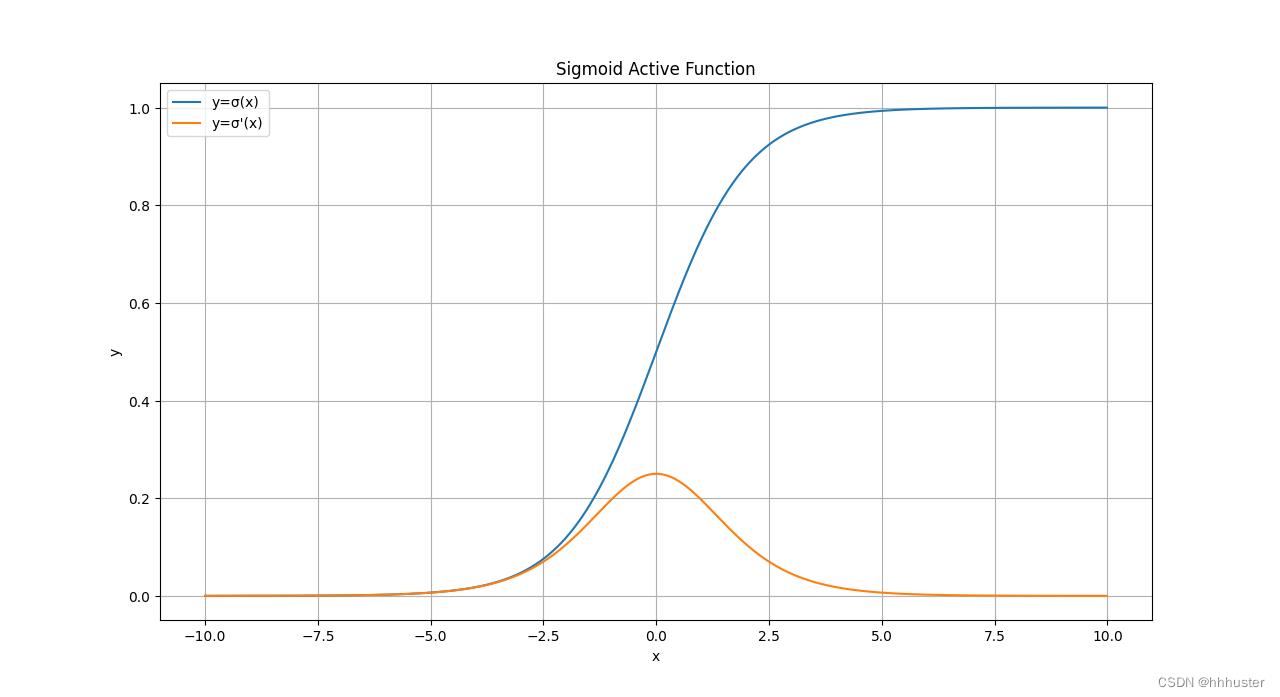
特点：易造成梯度消失（导数值小于1，多层相乘之后趋于0）；输出非0均值，收敛慢（一般数据都是服从标准正态分布的）；幂运算复杂，训练时间长
(2) tanh函数
y
=
t
a
n
h
(
x
)
=
e
x
−
e
−
x
e
x
−
e
−
x
=
1
−
e
−
2
x
1
+
e
−
2
x
,
d
y
d
x
=
t
a
n
h
′
(
x
)
=
1
−
y
2
y=tanh(x)=\\frace^x-e^-xe^x-e^-x=\\frac1-e^-2x1+e^-2x,~~~~\\fracdydx=tanh'(x)=1-y^2
y=tanh(x)=ex−e−xex−e−x=1+e−2x1−e−2x, dxdy=tanh′(x)=1−y2
简证：注意到
σ
(
x
)
+
σ
(
−
x
)
=
1
\\sigma(x)+\\sigma(-x)=1
以上是关于Tensorflow学习笔记：神经网络优化的主要内容，如果未能解决你的问题，请参考以下文章
Google深度学习笔记 TensorFlow实现与优化深度神经网络
机器学习笔记 - 深入了解TensorFlow模型优化工具包
在 ADAM 优化器的 CNTK 实现中，参数 alpha、beta1、beta2 和 epsilon 如何与学习率和动量相关