算法学习笔记
Posted gwpscut
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了算法学习笔记相关的知识，希望对你有一定的参考价值。
最近无意中看到一个算法的网站，看着感觉介绍得挺系统的，虽然做算法以及指导学生开发各种算法这么些年了，却没有真正系统的学习过（几年前啃过算法导论，但是苦于那蹩脚的中文翻译，也没有去看英文原文）。为此决定好好学习一下，本博文为本人学习下面网站的资料的学习记录，本博文仅为本人学习记录用，随着学习的过程也会不断更新此间内容。
https://labuladong.github.io/algo/
https://labuladong.github.io/algo/
目录
Chrome 刷题插件安装
正所谓工欲善其事，必先利其器，首先下载Chrome浏览器及其插件：
https://chrome.google.com/webstore/detail/leetcode-helper-by-labula/elafhogmnaapleckojedgipgmidneccg安装成功后，可以在插件列表看到插件图标：
点击插件图标可以弹出插件弹窗，包含刷新数据的按钮和很多有用的链接：
建议在 Chrome/商店安装的，这样会在新版本发布后自动更新。
LeetCode 版可以通过点击链接进入：https://leetcode.com/list/9zwo3ww5/
随便点进去一个
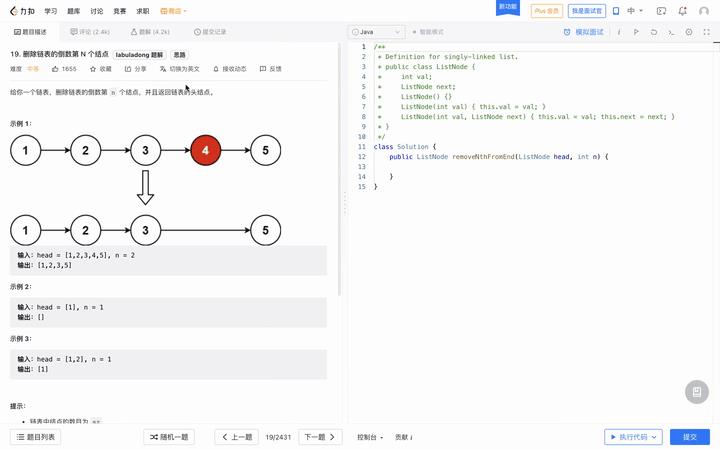
感觉确实是很不错，还有一些小的功能可以看下面。此处先不介绍，后面涉及再补上。
学习算法和刷题的框架思维
首先给出B站视频，建议看着视频来学习会更加直观。
【labuladong】学习数据结构和算法的框架思维
数据结构的存储方式只有两种：数组（顺序存储）和链表（链式存储）。
所谓的数组应该就是跟cpp里的差不多（连续的，顺序存储）。链表则是，数据+指向下一个数据的指针（非连续的，离散的存储）。
二者的优缺点如下：
数组由于是紧凑连续存储,可以随机访问，通过索引快速找到对应元素，而且相对节约存储空间。但正因为连续存储，内存空间必须一次性分配够，所以说数组如果要扩容，需要重新分配一块更大的空间，再把数据全部复制过去，时间复杂度 O(N)；而且你如果想在数组中间进行插入和删除，每次必须搬移后面的所有数据以保持连续，时间复杂度 O(N)。
链表因为元素不连续，而是靠指针指向下一个元素的位置，所以不存在数组的扩容问题；如果知道某一元素的前驱和后驱，操作指针即可删除该元素或者插入新元素，时间复杂度 O(1)。但是正因为存储空间不连续，你无法根据一个索引算出对应元素的地址，所以不能随机访问；而且由于每个元素必须存储指向前后元素位置的指针，会消耗相对更多的储存空间。
数据结构的基本操作：遍历 + 访问（就是存储与修改数据，即增删查改）
数据结构种类很多，但它们存在的目的都是在不同的应用场景，尽可能高效地增删查改。
典型的通过迭代，进行遍历访问：
void traverse(int[] arr)
for (int i = 0; i < arr.length; i++)
// 迭代访问 arr[i]
链表遍历框架，兼具迭代和递归结构：
/* 基本的单链表节点 */
class ListNode
int val;
ListNode next;
void traverse(ListNode head)
for (ListNode p = head; p != null; p = p.next)
// 迭代访问 p.val
void traverse(ListNode head)
// 递归访问 head.val
traverse(head.next);
基本的N叉树结构（更下一个section中实现的四叉树非常的像）：
/* 基本的 N 叉树节点 */
class TreeNode
int val;
TreeNode[] children;
void traverse(TreeNode root)
for (TreeNode child : root.children)
traverse(child);
基于图像像素强度来提取其四叉树结构
虽然整个系列还没学习完，但是正好最近项目需要用到提取图像的四叉树结构。
如下图所示。左图为图像，右图为其对应的深度图。根据对应的像素值或深度值获取对应的四叉树结构。
In most of the cases, pixels that share the same quadtree block in the intensity image also belongs to the same block in the depth map, but not vice versa. This means that pixels that are within the same quadtree block of the intensity image share similar intensity values and depth values.
此处尝试实现图（a）的效果。
实现的代码如下：
Tree.hpp
#ifndef _TREE_HPP_
#define _TREE_HPP_
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <queue>
// GLM Mathemtics
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
#include "glm/ext.hpp"
// Struct data of TreeNode
template <class T,int Child_num>
struct TreeNode
glm::vec3 _data;//color(像素值)
T _min;//left top node
T _max;//right bottom node
TreeNode<T, Child_num>* _children[Child_num]; //0 1 2 3 . the 4 children node in this Parent's node
TreeNode()
_data = glm::vec3(0, 0, 0);
for (auto i = 0; i < Child_num; i++)
_children[i] = NULL;
~TreeNode()
for (int i = 0; i < Child_num; i++)
delete _children[i];
;
//Class of the Tree
template <class T, int Child_num>
class Tree
public:
Tree() : _root(nullptr)
~Tree()
delete _root;
//Build the Tree
TreeNode<T, Child_num>* BuildTree(int depth, const T min, const T max, const int _minwidth, const int _minheight, const double _threshold)//输入为深度，（0，0）与（列、行）
depth = depth - 1;
//返回空指针
if (depth < 0) return nullptr;//返回空指针，当前构建的子树为空
//否则，先将此子树新建一个root元素，根据四个子树来更新root
TreeNode<T, Child_num>* root = new TreeNode<T, Child_num>;//初始化时_children为空的
T mid = T((min.x + max.x) / 2, (min.y + max.y) / 2);//获取中值
//更新max min（每次进入，当前的就会成为root，再有childern就是root，没有children就是leaf。而对于root需要更新_data，_min，_max）
root->_max = max;
root->_min = min;
// 看看是否满足一定的条件。只有满足的情况下才会进行子树的更新
cv::Mat tempMean, tempStddv;
double MEAN, STDDV;// mean and standard deviation of the flame region
//获得此时root对应的区域
cv::Mat flameRectRegion(image_data, cv::Rect(int(min.x), int(min.y), int(max.x) - int(min.x), int(max.y) - int(min.y)));
cv::cvtColor(flameRectRegion, flameRectRegion, cv::COLOR_RGB2GRAY);//转换为黑白
cv::meanStdDev(flameRectRegion, tempMean, tempStddv);
MEAN = tempMean.at<double>(0, 0);//均值
STDDV = tempStddv.at<double>(0, 0);//方差
// std::cout<<"STDDV="<<STDDV<<std::endl;
double STDDV_threshold=_threshold;//方差就是数据的分散程度（偏离均值）
if(STDDV>STDDV_threshold && (max.x-min.x>=2*_minwidth || max.y-min.y>=2*_minheight))
//更新四个子树
root->_children[0] = BuildTree(depth, min, mid,_minwidth, _minheight,_threshold);
root->_children[1] = BuildTree(depth, T(mid.x, min.y), T(max.x, mid.y),_minwidth, _minheight,_threshold);
root->_children[2] = BuildTree(depth, T(min.x, mid.y), T(mid.x, max.y),_minwidth, _minheight,_threshold);
root->_children[3] = BuildTree(depth, mid, max,_minwidth, _minheight,_threshold);
// //更新data
if (root->_children[0] != NULL)//当子树不为空，就是当前为root
//the root data is the average num of the 4 children's data.
root->_data.x = (root->_children[0]->_data.x + root->_children[1]->_data.x + root->_children[2]->_data.x + root->_children[3]->_data.x) / 4;
root->_data.y = (root->_children[0]->_data.y + root->_children[1]->_data.y + root->_children[2]->_data.y + root->_children[3]->_data.y) / 4;
root->_data.z = (root->_children[0]->_data.z + root->_children[1]->_data.z + root->_children[2]->_data.z + root->_children[3]->_data.z) / 4;
else//如果为空，就是没有进一步延伸了，那么就用原图赋值
cv::Mat my_mat(image_data, cv::Rect(int(min.x), int(min.y), int(max.x) - int(min.x), int(max.y) - int(min.y)));//(beginx beginy lenx leny)
cv::Mat channels[3];
split(my_mat, channels);//get the 3 channels of the Rect and RGB is the mean of the different channels of the Rect
root->_data.x = cv::mean(channels[0]).val[0];//求取算术平均值
root->_data.y = cv::mean(channels[1]).val[0];
root->_data.z = cv::mean(channels[2]).val[0];
//cout << glm::to_string(root->_data) << endl<<endl;
return root;
TreeNode<T, Child_num>* _root;
cv::Mat image_data;
;
typedef TreeNode<glm::vec2,4> QuadTreeNode;
typedef Tree<glm::vec2,4> QuadTree;
#endif /* _TREE_HPP_ */
调用代码块
void convert_quadtree_image(const cv::Mat& intensity_image, cv::Mat& quadtree_image_result)
QuadTree* QuadTree_handler = new QuadTree;
QuadTree_handler->image_data = event_intensity_image.clone();
int iterations=_iterations;//iterations（最深可以分割为多少）
ROS_WARN("Start build the Quadtree!");
QuadTreeNode* Root = QuadTree_handler->BuildTree(
iterations,
glm::vec2(0, 0),
glm::vec2(QuadTree_handler->image_data.cols, QuadTree_handler->image_data.rows),
_minwidth, _minheight, _threshold);
ROS_WARN("Build the Quadtree end!");
//out all the data in the QuadTree
// std::queue<QuadTreeNode*> S;
std::deque<QuadTreeNode*> S;
S.push_back(Root);//在末尾插入一个元素
while (!S.empty())
for (int i = 0; i < 4; i++)
if (S.front()->_children[i] != nullptr)//若这个children不是空的话，就会插入
S.push_back(S.front()->_children[i]);
//if the node is the leaf node , update the quadtree_image_result image.
//using the data: _min _max _data
if (S.front()->_children[0] == nullptr
&& S.front()->_children[1] == nullptr
&& S.front()->_children[2] == nullptr
&& S.front()->_children[3] == nullptr)//如果它的children都是空的，就证明当前的node不是root，而是leaf，那么就对quadtree_image_result进行赋值
// for (int i = S.front()->_min.x; i < S.front()->_max.x; i++)
//
// for (int j = S.front()->_min.y; j < S.front()->_max.y; j++)
//
// if (i >= 0 && i < event_intensity_image.cols && j >= 0 && j < event_intensity_image.rows)//保证不会越界
//
// quadtree_image_result.at<cv::Vec3b>(j, i)[0] = S.front()->_data.x;//B
// quadtree_image_result.at<cv::Vec3b>(j, i)[1] = S.front()->_data.y;//G
// quadtree_image_result.at<cv::Vec3b>(j, i)[2] = S.front()->_data.z;//R
//
//
//
// Add a black border around the given image quadrant.
if(_set_border)
cv::rectangle(quadtree_image_result, cv::Point(S.front()->_min.x, S.front()->_min.y), cv::Point(S.front()->_max.x, S.front()->_max.y), cv::Scalar(0, 0, 0), 1, 1, 0);
S.pop_front();//删除第一个元素
// delete QuadTree_handler;
// delete Root;
效果如下：
Experimental Record——Quadtree
对于图像相似度上，目前仅仅采用了求小区域内的方差，方差小于一定的阈值则认为该区域不需要再进一步分割。但是感觉这样设置并不是很好，跪求有想法的小伙伴给些建议哈～
参考资料
《算法秘籍》和《刷题笔记》。下载链接：https://pan.baidu.com/s/1PoG0Zxy7H64aXUM-Gj0UuA?pwd=541i 提取码：541i
以上是关于算法学习笔记的主要内容，如果未能解决你的问题，请参考以下文章