什么样的图最小生成树唯一？

Posted 2023-04-30

如题，请以简答形式回答

如果一个图的各个边的权值各不相同，那么它的最小生成树是唯一的。

n个点用n-1条边连接，形成的图形只可能是树。可以这样理解：树的每一个结点都有一个唯一的父亲，也就是至少有n条边，但是根节点要除外，所以就是n-1条边。

那么，对于一张n个点带权图，它的生成树就是用其中的n-1条边来连接这n个点，那么最小生成树就是n-1条边的边权之和最小的一种方案，简单的理解，就是用让这张图只剩下n-1条边，同时这n-1条边的边权总和最小。红边即为此图的最小生成树。

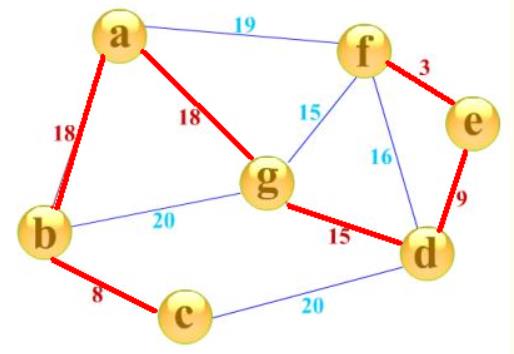
树形图的概念

无圈且连通的无向图称为树。树一般记为T。作为树定义还可以有以下几种表述：

（1）T 连通且无圈或回路。

（2）T无圈且有n－1条边（如果有n个结点）。

（3）T连通有n－1条边。

（4）T无回路，但不相邻的两个结点之间联以一边，恰得一个圈。

（5）T连通，但去掉T的任意一条边，T就不连通了。（亦即在点集合相同的图中，树是含边数最少的连通图。）

（6）T的任意两个结点之间恰有一条初等链。

参考技术A 所有权值都不相等，或者有相等的边但是在构造生成树的过程中权值相等的边都被纳入到了生成树中，其最小生成树唯一。——天勤 参考技术B

先正常求出最小生成树，再求次小生成树（具体可以枚举图上其他边加到树里，同时删去重复的边，找到权值和最小的删边方法），如果求出次小生成树的权值和与最小生成树不相等，则最小生成树唯一，否则不唯一。

参考技术C 在一个带权无向连通图G中，对G的某棵最小生成树T，对于不在T中的每一条边e，e的权值总是T与e合并所产生的环上各条边权中的唯一最大值 <==> 此图中最小生成树唯一

这是充分必要条件了。
无等权边是充分不必要条件。 参考技术D 当带权连通图的任意一个环中所包含的权值均不相同，其MST是唯一的。---出自王道

连通图的最小生成树是否唯一的？

如题！
http://hi.baidu.com/mimicekoo/album/item/5c64400fe6dc153f6059f307.html
帮我看看。。谢谢了！

视情况而定，有的是唯一的，有的不是唯一的，所以可以回答不是唯一的。你最好补充个例题，我给你分析一下。
你给的图有三种最小生成树,我不会画图，我把每个图包括的边给出来，你自己画一下吧：1.<a,c>;<a,b>;<b,d>;<d,g>;<d,h>;<e,f>;<f,g>
2.<a,c>;<a,b>;<c,d>;<d,g>;<d,h>;<e,f>;<f,g>
3.<a,c>;<a,b>;<c,h>;<d,g>;<d,h>;<e,f>;<f,g>

发一个最小生成树算法：
最小生成树Prim算法2006-10-21 14:51对于网络，其生成树中的边也带权，将生成树各边的权值总和称为生成树的权，并将权值最小的生成树称为最小生成树（Minimun Spanning Tree），简称为MST。
Prim算法的基本思想是：

(1) 在图G=(V, E) （V表示顶点 ，E表示边）中，从集合V中任取一个顶点（例如取顶点v0）放入集合 U中，这时 U=v0，集合T(E)为空。

(2) 从v0出发寻找与U中顶点相邻（另一顶点在V中）权值最小的边的另一顶点v1，并使v1加入U。即U=v0,v1 ，同时将该边加入集合T(E)中。

(3) 重复(2)，直到U = V为止。

这时T(E)中有n-1条边，T = (U, T(E))就是一棵最小生成树。 参考技术A 不是唯一的，但是不同的最小部分树的各枝加起来的总和是相等的，因此这也不失为一种检验你对错的办法。