直观理解-梯度下降及MIT自适应控制律

Posted 2022-12-16 ayuan0211

具体解释了什么是梯度，以及梯度如何应用于MIT自适应控制律，为后续基于梯度法的模型参考自适应控制做铺垫，如果可以理解的，可以自动跳过。

目录

一、梯度

二、MIT自适应律

一、梯度

什么是梯度呢？梯度可以理解为一个向量，具有方向性。

若是一维函数，y=f(x)，那么梯度就是f函数的导数，，物理意义上就是函数f的切线方向。

若是二维函数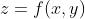，,那么梯度就是f函数的偏导数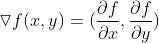，,物理意义上就是函数f曲面的切面，而偏导数相当于一个自变量不变，而另外一个自变量变化，整个函数中相当于仅有一个自变量，问题即可转化为一维函数。

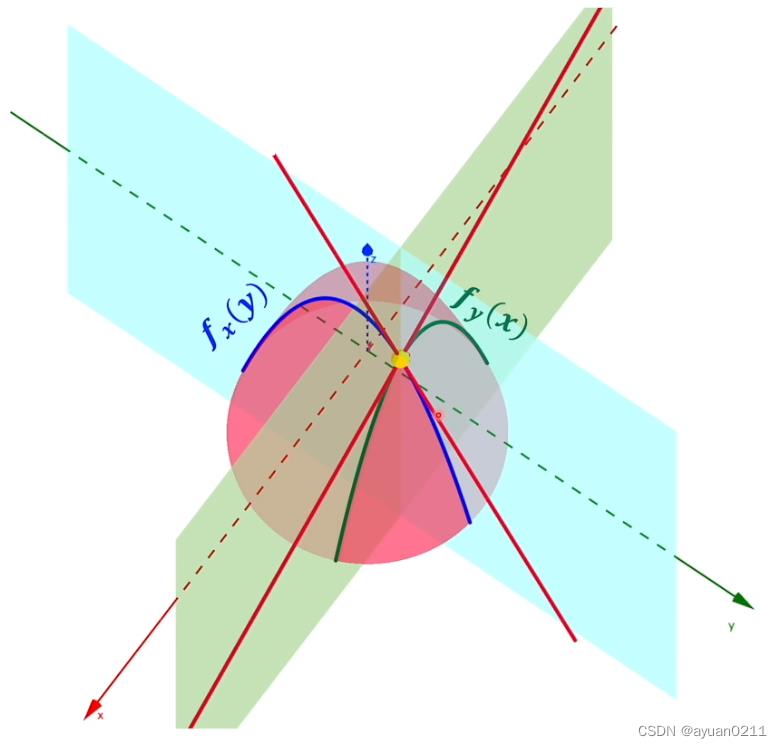
梯度是参数改变速度最快的方向。因此采用梯度方法可以快速收敛到自适应律（损失函数）的目标内。

二、MIT自适应律

假设参考模型输出和系统实际输出之差为e，即模型误差，被控对象未知或慢时变参数为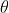[优化参数]。

被控对象的控制目标为：调整控制器参数，使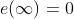，即误差收敛。

性能指标函数一般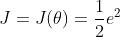为，自变量为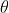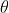，的维数取决于你需要优化的参数有多少个，如果你需要优化的参数有n个则为n为函数。

使用梯度下降法能够使J快速收敛到最小，这里需要使用负梯度，使得函数是朝着小值变化。

则需要求J关于的偏导：

在此基础上需要确定梯度下降的步长，如果下降太快，容易陷入局部最优，所以需要选取合适的，即梯度系数。

可表示为：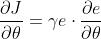

取负梯度方向，则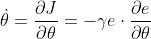

参考资料：

[5分钟深度学习] #01 梯度下降算法_哔哩哔哩_bilibili

如何理解“梯度下降法”？什么是“反向传播”？通过一个视频，一步一步全部搞明白_哔哩哔哩_bilibili

系统辨识与自适应控制MATLAB仿真（第三版）

相关下载链接【不是我自己的资源，只是搜索的~】：系统辨识与自适应控制Matlab仿真 含pdf书和源代码-北航版下载-CSDN社区