一假期番外篇——动态规划，Leetcode121

Posted 2022-12-16 小可爱的大笨蛋

春节期间，根本没时间去做项目，只能开启刷题模式，决定以Leetcode为平台，入坑算法，重新学习动态规划。

选择的题目是Leetcode的第121题：买卖股票的最佳时机。

这是Leetcode的题目描述，接下来就开始解决。

刚开始考虑的是暴力破解：假设当前为买入，之后的所有都为卖出，算出每一个的差值，返回最大差值。

    public static int maxProfit(int[] prices) 
    	int n = prices.length;
    	int max = 0;
    	for(int i=0;i<n;i++) 
    		for(int j=i+1;j<n;j++) 
    			int diff = prices[j] - prices[i];
    			if(diff < 0) diff = 0;
    			if(max < diff) max = diff;  			
    		
    	
    	return max;
    

提交运行一下

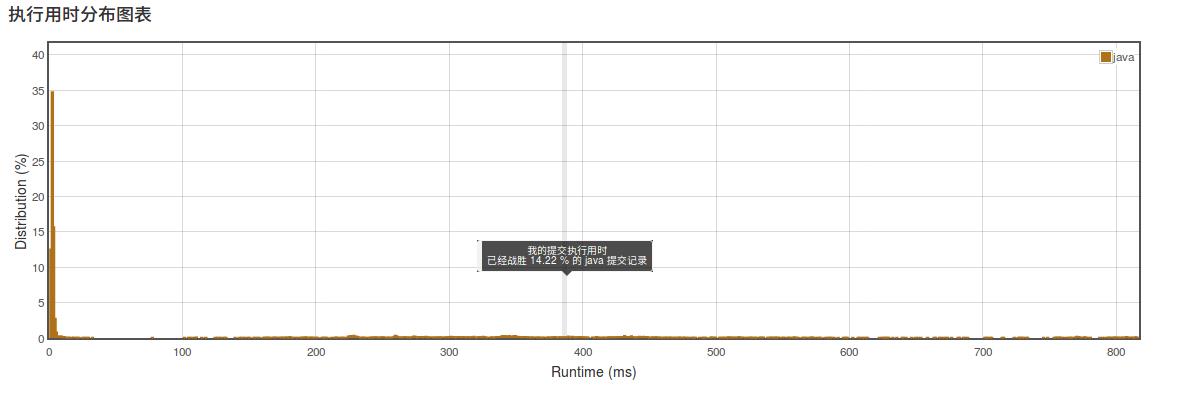
有点水，接下来优化一下，暴力破解的时间复杂度是O(n2)，那就想办法优化成时间复杂度为O(n)：

我的思路是这样的：加入4个变量，max,min,first,last,4个变量的作用分别是max指向最大的，min指向最小的，first是买入的位置，last是卖出的位置，如果last比first小的话，那就让last指向first，然后max等于min，每次计算一次差值，返回最大的差值。代码如下：

    public static int maxProfit_p(int[] prices) 
    	if(prices.length <= 0) 
    		return 0;
    	
    	int min,max;
    	int diff = 0;
    	min = max =prices[0];
    	int first=0,last=0;
    	for(int i=1;i<prices.length;i++) 
    		if(max < prices[i]) max = prices[i]; last=i;
    		if(min > prices[i]) min = prices[i]; first =i;
    		if(last < first) last = first; max = min;
    		if(diff < (max - min)) diff = max-min;
    	
    	return diff;
    

提交一下：

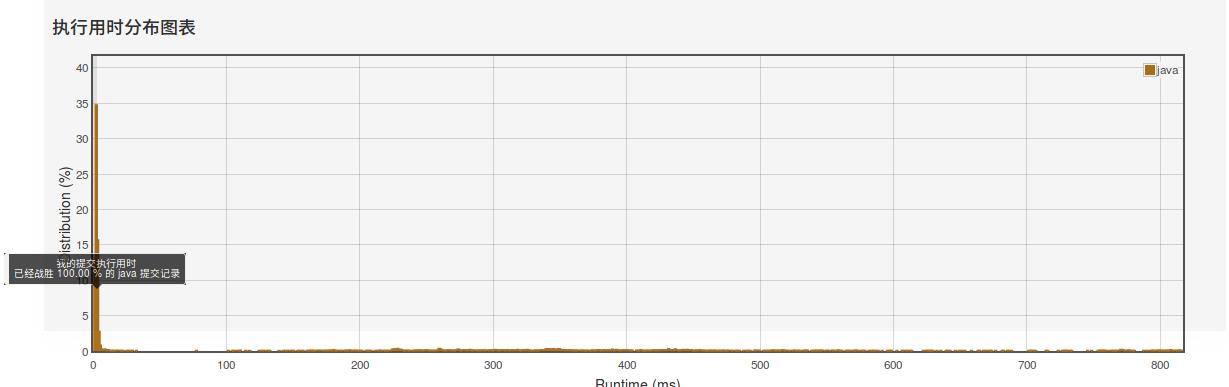
发现已经达到了100%，但这不是我们想要的，我们想要的是使用动态规划，接下来就是动态规划。

首先，在计算任意一个位置的最佳时机时应该有两种选择，即当前点是最佳时机，或者不是最佳时机，如果当前点是最佳时机，应该等于当前时机的价格减去之前最小的价格，如果不是最佳时机，就等于它前一个的最佳时机。OK，直接上代码：

  public static int maxProfit_dp(int[] prices) 
    	int minP = Integer.MAX_VALUE;  // 最小的价格
    	int maxDiff = 0; // 最大的差值
    	for(int i=0;i<prices.length;i++) 
    		if(minP > prices[i]) minP = prices[i];
    		if(maxDiff < (prices[i] - minP)) maxDiff = prices[i] - minP;
    	
    	return maxDiff;
    

提交一下：

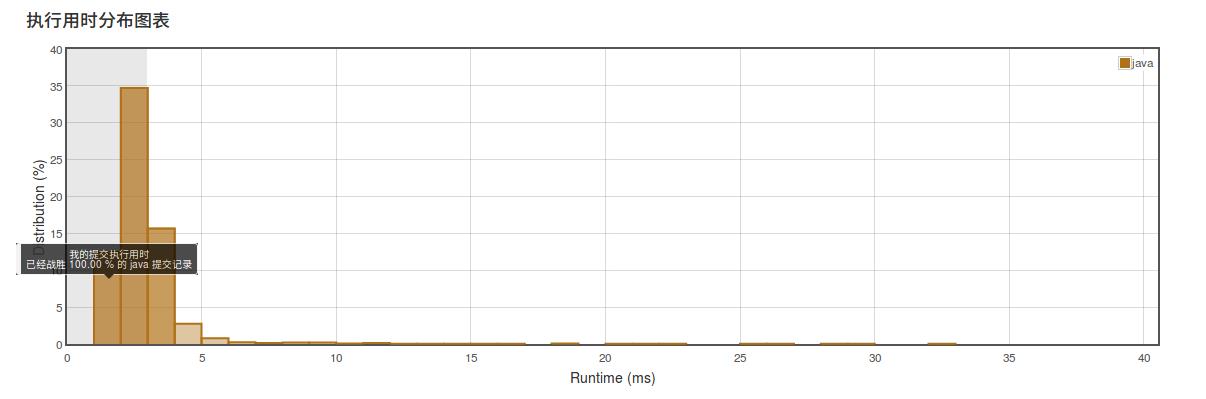
万事大吉。

总结：重点在于总结出问题过程中的讲问题转换成子问题，然后写出方程的过程。