Leetcode 1671. Minimum Number of Removals to Make Mountain Array

Posted 2022-12-14 SnailTyan

文章作者：Tyan
博客：noahsnail.com  |  CSDN  |  简书

1. Description

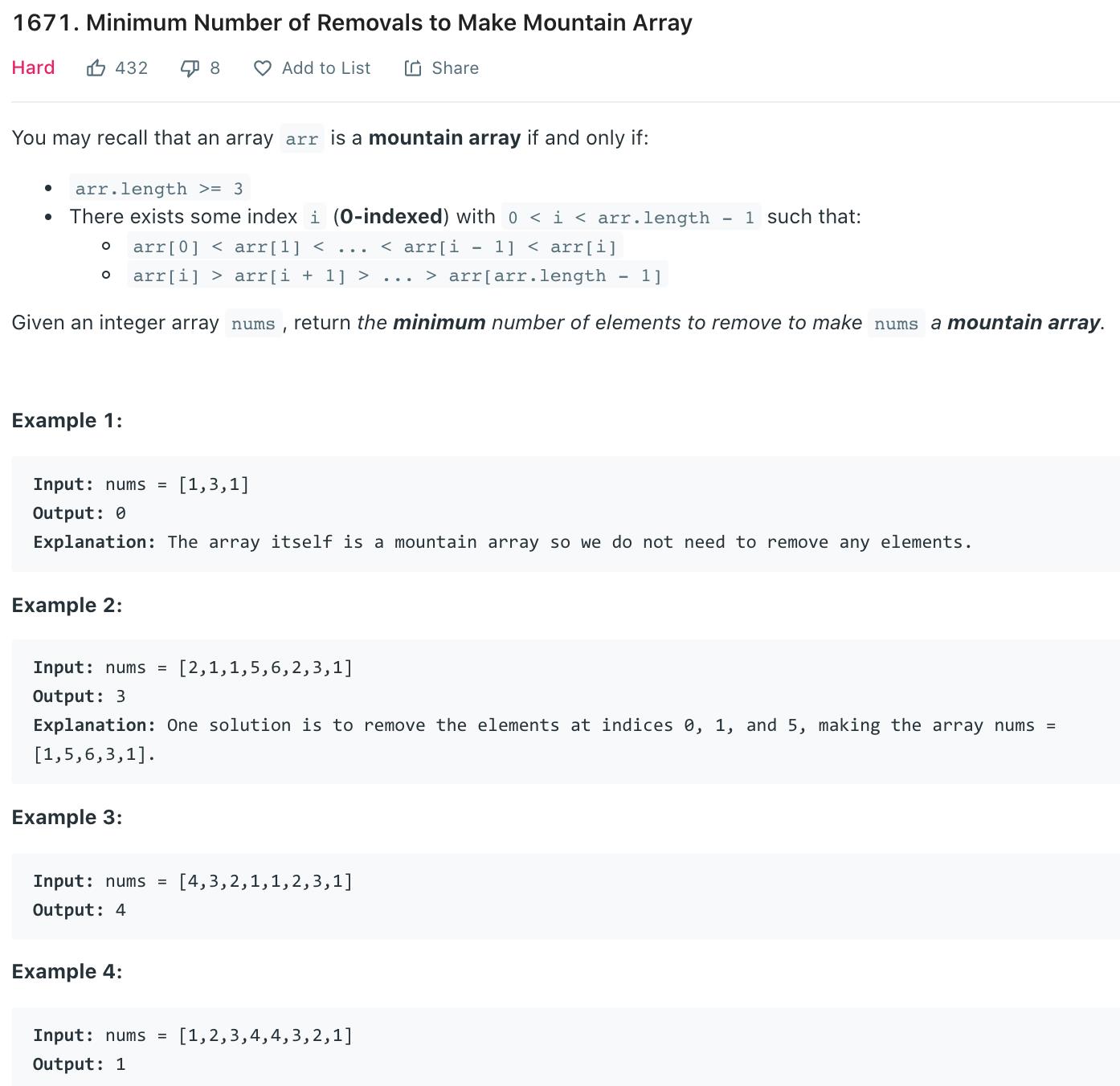
2. Solution

**解析：**Version 1，分别以数组中的元素作为中心点，在左右两侧分别求最长递增子序列，根据左右两侧的最长递增子序列的长度求出山脉的长度，则要删除的元素个数为数组长度减去最长的山脉长度，速度太慢。Version 2在Version 1的基础上进行了优化，分别求出数组正序和逆序各个位置的最长递增子序列，然后跟Version 1类似，累加左右对应位置的最长递增子序列的长度，即为山脉的长度，则要删除的元素个数为数组长度减去最长的山脉长度，速度明显有了大幅提升。

• Version 1

class Solution:
    def minimumMountainRemovals(self, nums: List[int]) -> int:
        n = len(nums)
        maximum = 0
        for index in range(1, n - 1):
            left = [nums[index]]
            for i in range(index - 1, -1, -1):
                if nums[i] >= nums[index] or nums[i] == left[0]:
                    continue
                elif nums[i] < left[0]:
                    bisect.insort(left, nums[i])
                else:
                    pos = bisect.bisect(left, nums[i])
                    left[pos-1] = nums[i]
            if len(left) < 2:
                continue
            right = [nums[index]]
            for i in range(index+1, n):
                if nums[i] >= nums[index] or nums[i] == right[0]:
                    continue
                if nums[i] < right[0]:
                    bisect.insort(right, nums[i])
                else:
                    pos = bisect.bisect(right, nums[i])
                    right[pos-1] = nums[i]
            if len(right) > 1:
                maximum = max(maximum, len(left) + len(right) - 1)
        return n - maximum

• Version 2

class Solution:
    def minimumMountainRemovals(self, nums: List[int]) -> int:
        n = len(nums)
        maximum = 0
        left = self.LIS(nums)
        right = self.LIS(nums[::-1])
        for i in range(n):
            if left[i] > 1 and right[n-i-1] > 1:
                maximum = max(maximum, left[i] + right[n-i-1] - 1)
        return n - maximum


    def LIS(self, nums):
        n = len(nums)
        dp = [1] * n
        arr = [nums[0]]
        for i in range(1, n):
            if nums[i] > arr[-1]:
                arr.append(nums[i])
            else:
                pos = bisect.bisect_left(arr, nums[i])
                arr[pos] = nums[i]
            dp[i] = len(arr)
        return dp

Reference

1. https://leetcode.com/problems/minimum-number-of-removals-to-make-mountain-array/