数据结构 -- 队列
Posted 庸人冲
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构 -- 队列相关的知识,希望对你有一定的参考价值。
文章目录
什么是队列
队列(queue)是只允许在一端进行插入操作,而另一端进行删除操作的线性表结构。
队列是一种先进先出的(First In First Out)的线性表,简称FIFO,允许插入的一段称为队尾,允许删除的一段称为队头。
假设存在队列 q=(a1,a2,a3…an), 则a1为队头元素,an为队尾元素,删除时总是删除队头元素,插入时,总是在队尾元素后插入。
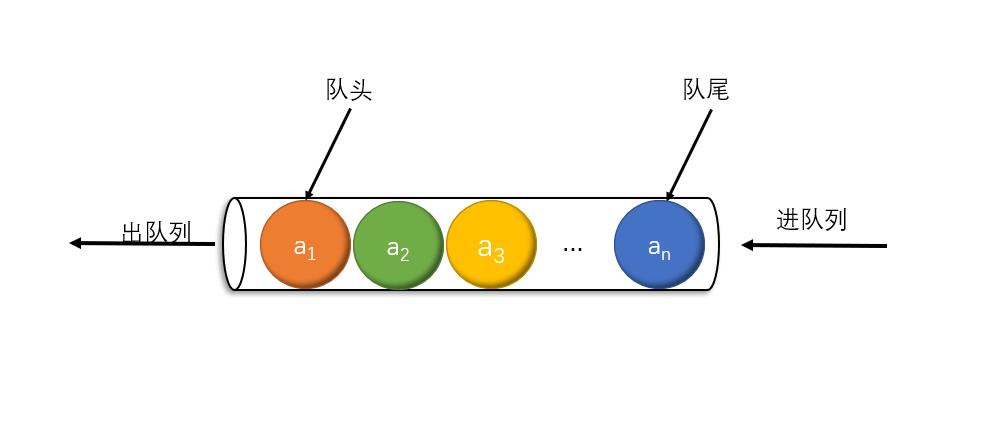
队列的顺序存储方式
队列可以使用数组(顺序表)或者链表的方式存储数据,本章介绍以数组的方式如何实现队列结构。
假设一个队列有n个元素,则需要创建一个长度大于n的数组作为容器,然后将队列的元素按照排队的顺序存放在数组中,我们可以按照从下标0的位置开始向后存储直到下标为n-1的位置结束,数组下标0的位置就是队头,下标n-1的位置就是队尾。当进行添加元素的操作时不需要移动队列中任何元素,只需要在队尾元素后的下标处添加新元素即可,添加元素的时间复杂度为O(1)。
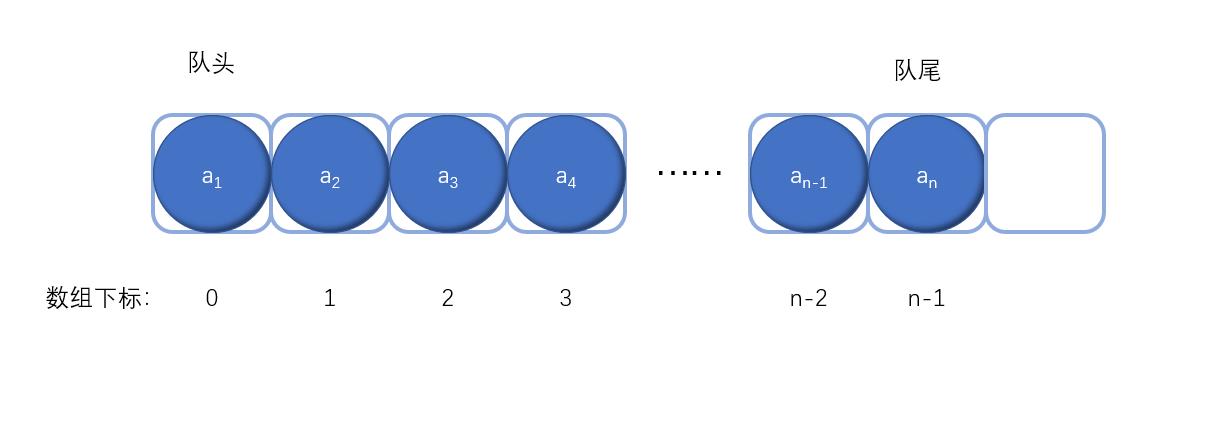
以上操作其实就是简单的给数组赋值,不过当我们删除队头元素时需要将其后的元素整体前移(顺序表的操作)这样删除元素的时间复杂度就是O(n)。
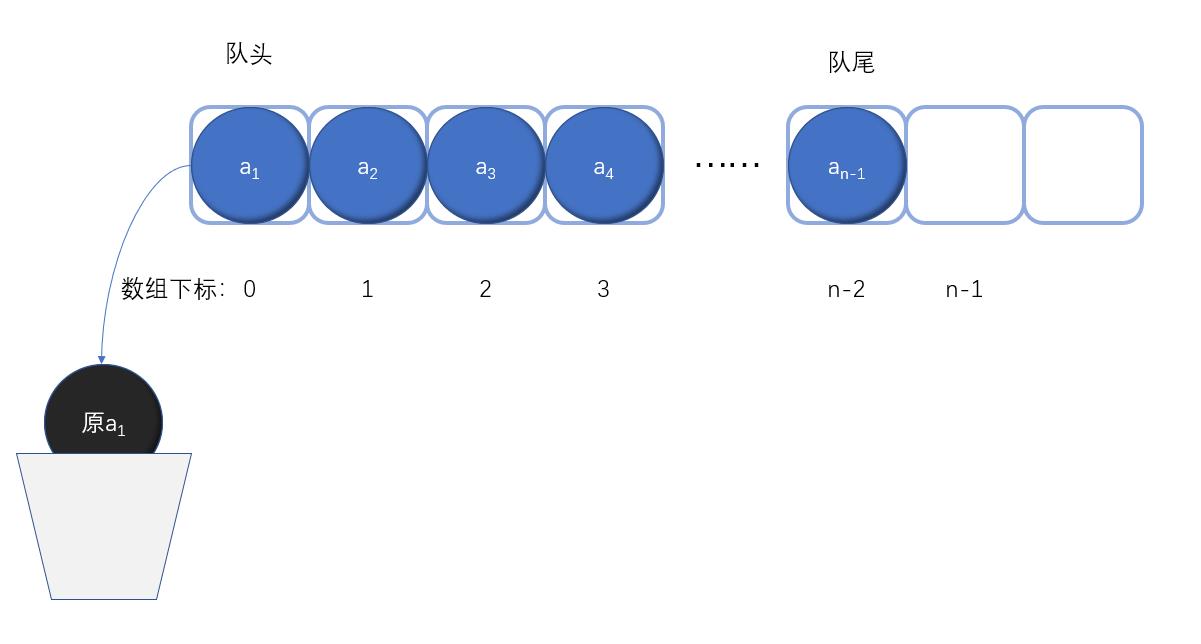
为了可以降低删除元素的时间复杂度,我们可以不把队头位置限制在数组下标为0处,也就是删除当前的队头元素后,后一个元素就是队头元素不再进行移动,而当队尾元素被删除时,即为空队列。
需要完成上述的述操作我们得引入两个变量来标记队头位置和队尾位置。不妨使用两个整型变量front、rear作为“指针”存放队头元素的下标和队尾元素的下标,但是当只有一个元素时,front和rear会指向同一个元素,所以为了避免队头和队尾重合使得处理变得麻烦,我们可以让rear存放队尾元素后一个位置的下标。这样当front和rear指向同一个位置时表示为空队列。
假设有一个长度为5的数组,在初始的空队列状态,front和rear都指向了下标0的位置。
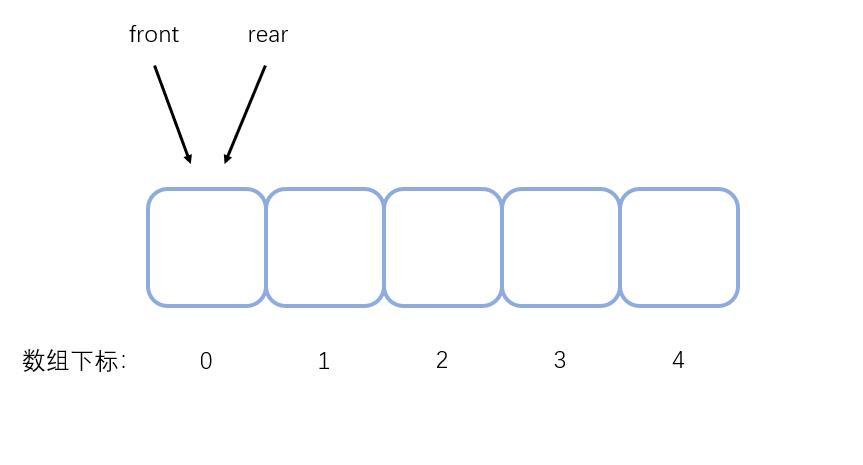
每向队列添加一个元素,front不变,rear会向后移动到后一个位置,假如添加4个元素进入数组。则rear会指向下标4的位置。
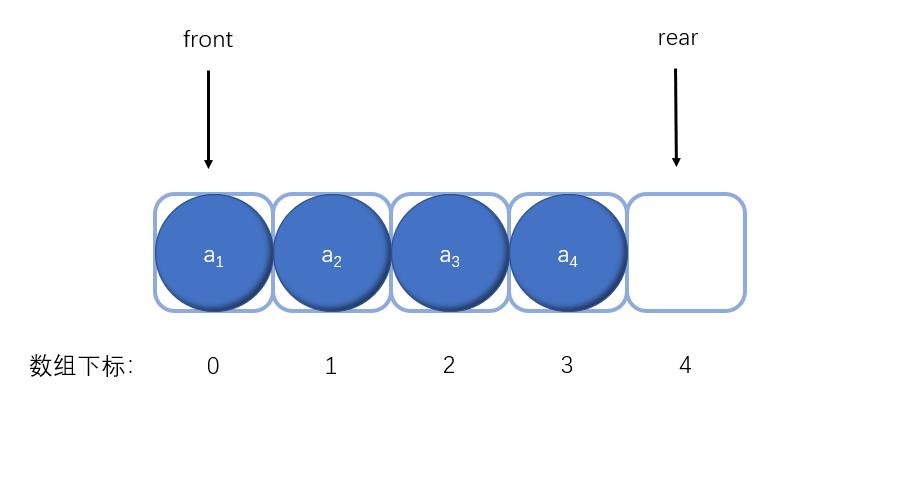
删除元素时,front会向后移动指向新的队头元素,rear不变,假如删除2个元素,front会指向下标为2的位置,此时a3为队头元素。
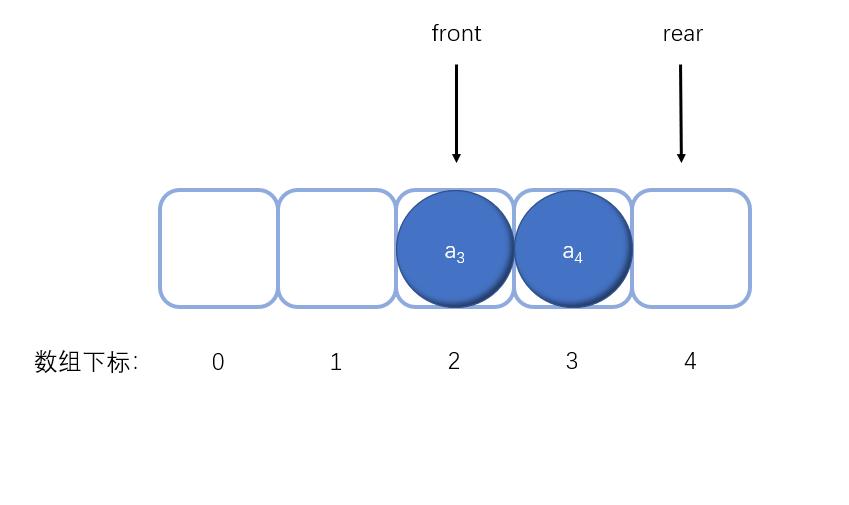
此时又会出现一个问题,当继续添加元素时,rear会指向数组外的位置,此时不能再继续添加元素,否则就会越界访问,但是front之前被删除元素的空间还空着却无法使用,这样的队列不就变成一次性的结构。所以为了解决这些问题,下面将介绍循环队列。
循环队列
解决上面问题的方式是当rear指向数组末尾再向后移动时,让rear重新回到下标为0的位置处,使得数组的首位相接形成环形,那么只要元素的总个数不超过数组的长度,这个队列就可以一直使用。
假设再上面的基础上继续添加a5元素,a5被添加到下标为4的位置,rear指向了下标为零的位置0。
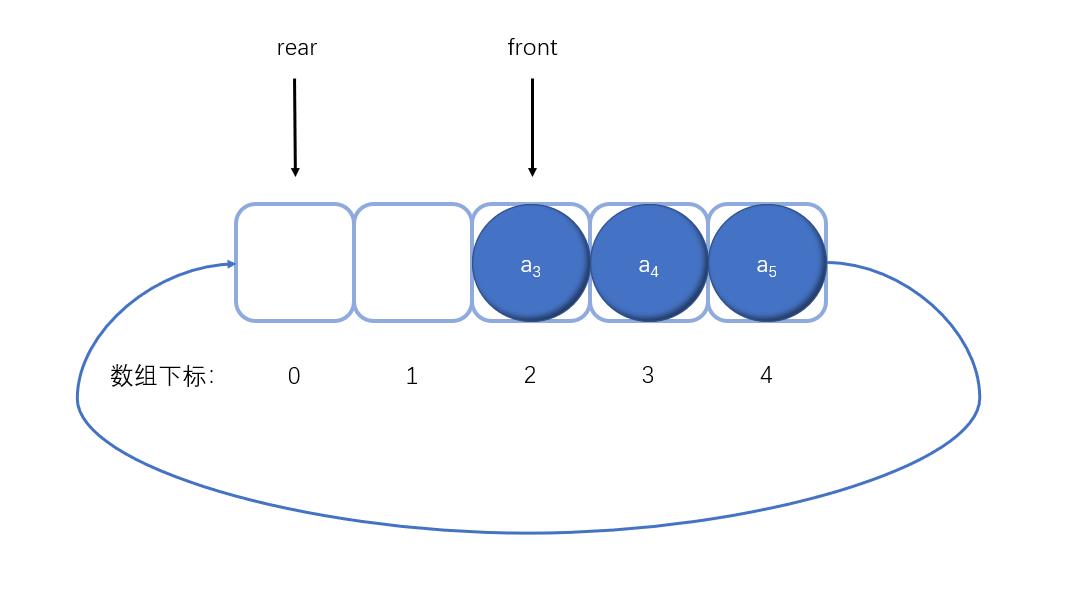
可以很容易发现,如果再继续添加2个元素,rear和front就会指向同一个元素a3,而之前说过,当rear和front指向同一个元素时表示空队列状态,现在又可以表示为满队列状态,那么该如何判断当 rear == front 时,是空队列还是满队列呢?
一种方式是,将队头元素的前一个位置的元素留空(不使用),这样当rear指向数组前一个位置时就表示队列已满,而rear == front表示空队列的判断依然保持不变。(注意:因为是环形链表,当队头元素的位置在下标为0处时,它的前一个位置就是数组的最后一个位置)
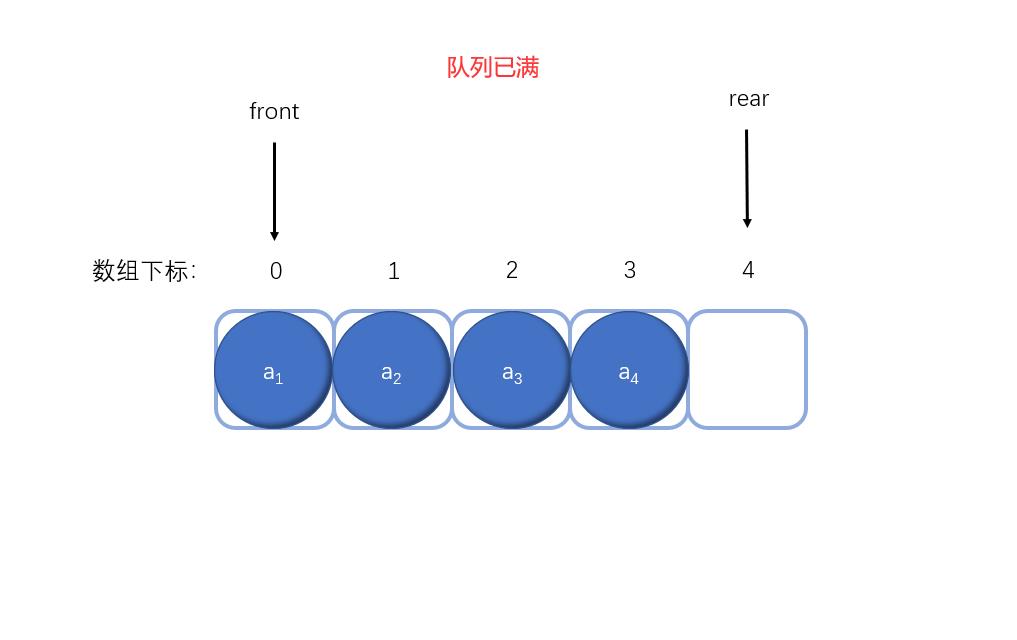
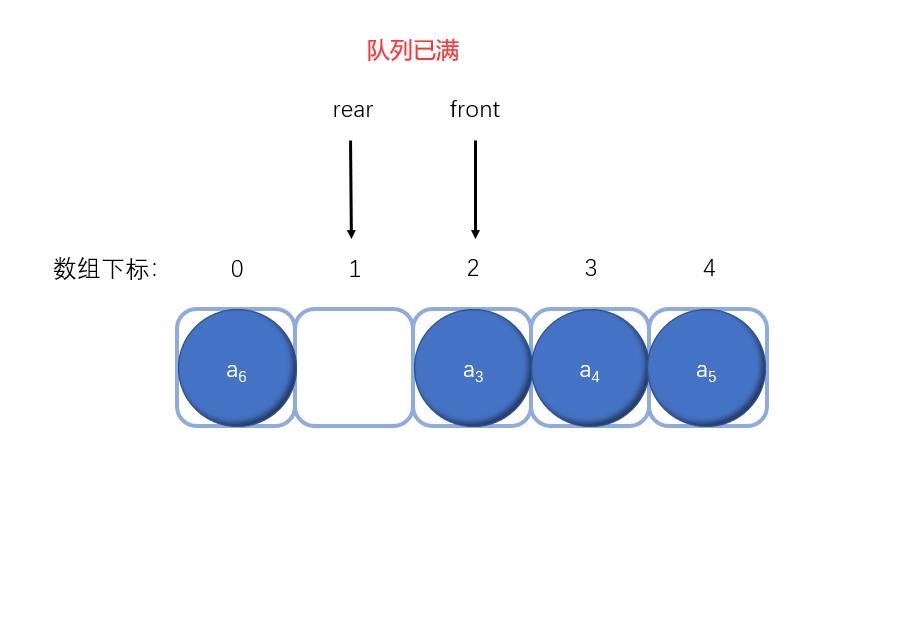
通过上图可以发现,当队列已满时rear可能大于front,也能小于front,那么判断队列是否满的条件应该是什么呢?
当rear < front时,rear + 1 == front,则说明队列已满,而当rear > front时,如果队列已满,rear + 1就会越界了,为了防止越界,需要把rear+1的取值范围控制在[0,队列最大容量)之间,所以假设使用变量maxSize存放队列最大容量,则判断条件为 (rear+1) % maxSize ,这种计算方法无论rear < front 还是 rear > front 都能正确的判断队列是否已满。
这种取模的解决思路,还可以用来计算当前队列中元素的个数:
当rear > front,那么 rear - front 得到的就是队列元素个数。
当rear < front,那么需要分别计算 [front,maxSize] 和 [0,rear] 这两个区间的元素个数。
- [front,maxSize] 的元素个数 == maxSize - front。
- [0,rear] 的元素个数 == rear - 0。
再将两个等式合并得到当前队列的元素个数 == rear - front + maxSize,可以发现比rear > front的计算公式多加了maxSize,为了使两个条件都能公用一个计算公式,还是需要 % maxSize 来防止当rear > front时会出现下标越界情况。
因此计算队列长度的公式为:(rear - front + maxSize ) % maxSize
代码实现
上面讲了那么多,接下来看看如何用代码实现环形队列的基本功能。
循环队列的顺序存储结构
class CircleQueue<E>
// 【定义队列结构】
private E[] data; // 存放队列数据的容器
private int maxSize; // 数组的最大容量
private int front; // 队列头, 初始为0, 指向队列首元素
private int rear; // 队列尾, 初始为0, 指向队列尾元素后一位置
public CircleQueue(int maxSize)
this.maxSize = maxSize;
data = (E[])new Object[maxSize]; // 创建maxSize大小的数组
判断队列是否已满
/**
* 判断队列是否已满, 环形队列中front前的一个空间被保留(不使用), 当front == 0 时, front前一个空间是数组的最后一个空间。因此当rear指向了front前的一个位置,说明队列已满。
* 即 (rear + 1) % maxSize == front, 取模运算时控制rear+1的取值范围在[0,maxSize)之间
* @return 已满返回true, 未满返回false
*/
public boolean isFull()
return (rear + 1) % maxSize == front; // rear + 1, 数组留空一个元素
判断队列是否为空
/**
* 判断队列是否为空, 当front前的一个位置被留空时, 则只有队列为空的情况下, rear == front, 因此判断条件为此等式。
* @return 为空返回true, 不为空返回false
*/
public boolean isEmpty()
return rear == front;
向队列中添加元素
/**
* 向队列中添加元素: 添加元素的位置在队尾处, 即当前rear指向的位置。
* @param e 待添加元素
* @return 队列已满返回 false, 添加成功返回 true
*/
public boolean addQueue(E e)
if(isFull()) return false;
data[rear] = e; // 将元素添加至队尾
rear = (rear + 1) % maxSize; // rear向后移动, 在[0,maxSize)间循环取值
return true;
删除队列中的元素
/**
* 删除队列中的元素: 删除元素的位置在队列头处, 即当前front指向的位置
* @return 队列为空返回null, 删除成功返回被删除元素
*/
public E delQueue()
if(isEmpty()) return null;
E value = data[front]; // 保存被删除元素
front = (front + 1) % maxSize; // front向后移动, 在[0,maxSize)间循环取值
return value; // 返回被删除元素
获取队头元素
/**
* 返回队头元素
* @return 队列为空返回null, 队列不为空返回队头元素
*/
public E getHead()
if(isEmpty()) return null;
return data[front];
获取队列元素个数
/**
* 获取队列中存在元素的个数, 虽然是环形队列, 但元素依然可以视为保存在 [front,rear) 间
* 因此, 可以分成两种情况:
* 情况一: rear > front时, size == rear - front。
* 情况二: rear < front时, size == (rear - 0) + (maxSize - front) = rear - front + maxSize
* 将两种情况综合得到: size == (rear - front + maxSize) / maxSize
* @return
*/
public int getSize()
return (rear - front + maxSize) % maxSize;
遍历元素
/**
* 元素存放在[front,rear)之间, 可以把环形想象成从front开始到rear前结束的一条线, 那么起点就是front, 终点就是rear前。
* 当front != rear时, 输出当前元素。
* 接着front向后移动, 同样需要进行取模使得front在[front,rear)之间循环取值
* 当front == rear时, 说明遍历结束, 退出循环。
*/
public void showQueue()
int begin = front;
while(begin != rear)
System.out.println(data[begin]);
begin = (begin + 1) % maxSize;
整体代码
package queue;
import org.junit.jupiter.api.Test;
import java.util.Scanner;
class CircleQueue<E>
// 【定义队列结构】
private E[] data; // 存放队列数据的容器
private int maxSize; // 数组的最大容量
private int front; // 队列头, 初始为0, 指向队列首元素
private int rear; // 队列尾, 初始为0, 指向队列尾元素后一位置
public CircleQueue(int maxSize)
this.maxSize = maxSize;
data = (E[])new Object[maxSize];
// 【功能实现】
/**
* 判断队列是否已满, 环形队列中front前的一个空间被保留(不使用), 当front == 0 时, front前一个空间是数组的最后一个空间。因此当rear指向了front前的一个位置,说明队列已满。
* 即 (rear + 1) % maxSize == front, 取模运算时控制rear+1的取值范围在[0,maxSize)之间
* @return 已满返回true, 未满返回false
*/
public boolean isFull()
return (rear + 1) % maxSize == front; // rear + 1, 数组留空一个元素
/**
* 判断队列是否为空, 当front前的一个位置被留空时, 则只会在队列为空的情况下, rear == front, 因此判断条件为此等式。
* @return 为空返回true, 不为空返回false
*/
public boolean isEmpty()
return rear == front;
/**
* 向队列中添加元素: 添加元素的位置在队尾处, 即当前rear指向的位置。
* @param e 待添加元素
* @return 队列已满返回 false, 添加成功返回 true
*/
public boolean addQueue(E e)
if(isFull()) return false;
data[rear] = e; // 将元素添加至队尾
rear = (rear + 1) % maxSize; // rear向后移动, 在[0,maxSize)间循环取值
return true;
/**
* 删除队列中的元素: 删除元素的位置在队列头处, 即当前front指向的位置
* @return 队列为空返回null, 删除成功返回被删除元素
*/
public E delQueue()
if(isEmpty()) return null;
E value = data[front]; // 保存被删除元素
front = (front + 1) % maxSize; // front向后移动, 在[0,maxSize)间循环取值
return value; // 返回被删除元素
/**
* 返回队头元素
* @return 队列为空返回null, 队列不为空返回队头元素
*/
public E getHead()
if(isEmpty()) return null;
return data[front];
/**
* 获取队列中存在元素的个数, 虽然是环形队列, 但元素依然可以视为保存在 [front,rear) 间
* 因此, 可以分成两种情况:
* 情况一: rear > front时, size == rear - front。
* 情况二: rear < front时, size == (rear - 0) + (maxSize - front) = rear - front + maxSize
* 将两种情况综合得到: size == (rear - front + maxSize) / maxSize
* @return
*/
public int getSize()
return (rear - front + maxSize) % maxSize;
/**
* 元素存放在[front,rear)之间, 可以把环形想象成从front开始到rear前结束的一条线, 那么起点就是front, 终点就是rear前。
* 当front != rear时, 输出当前元素。
* 接着front向后移动, 同样需要进行取模使得front在[front,rear)之间循环取值
* 当front == rear时, 说明遍历结束, 退出循环。
*/
public void showQueue()
int begin = front;
while(begin != rear)
System.out.println(data[begin]);
begin = (begin + 1) % maxSize;
// 测试模块
public class CircleArrayQueueTest1
public void menu()
System.out.println("1. 添加数据");
System.out.println("2. 删除数据");
System.out.println("3. 获取头数据");
System.out.println("4. 获取数据总数");
System.out.println("5. 显示所有数据");
System.out.println("6. 退出");
System.out.print("输入>: ");
@Test
public void testArrayQueue()
CircleQueue<Integer> circleQueue = new CircleQueue<>(5);
Scanner scan = new Scanner(System.in);
boolean loop = true;
while (loop)
menu();
char ipt = scan.next().charAt(0);
switch (ipt)
case '1': // 添加数据
System.out.print("请输入添加的数据:>");
if (circleQueue.addQueue(scan.nextInt()))
System.out.println("添加成功");
else
System.out.println("队列已满");
break;
case '2': // 删除数据
Integer del = circleQueue.delQueue();
if(del == null)
System.out.println("队列为空");
else
System.out.println("数据: " + del + ", 已被删除");
break;
case '3': // 获取头数据
Integer head = circleQueue.getHead();
if(head == null)
System.out.println("队列为空");
else
System.out.println("头数据为: " + head);
break;
case '4': // 获取数据总数
System.out.println("队列数据总数: " + circleQueue.getSize());
break;
case '5': // 显示所有数据
circleQueue.showQueue();
break;
case '6': // 退出
loop = false;
scan.close();
System.out.println("退出成功");
break;
default:
System.out.println("输入错误");
以上是关于数据结构 -- 队列的主要内容,如果未能解决你的问题,请参考以下文章