深度学习Deep Learning（03）：权重初始化问题1_Sigmoid anhSoftsign激励函数

Posted 2022-12-14 莫失莫忘Lawlite

二、权重初始化问题1_Sigmoid\\tanh\\Softsign激励函数

• github地址：https://github.com/lawlite19/DeepLearning_Python

1、说明

• 参考论文：http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
• 或者查看这里，我放在github上了：https://github.com/lawlite19/DeepLearning_Python/blob/master/paper/Understanding%20the%20difficulty%20of%20training%20deep%20feedforward%20neural%20networks.pdf
• 这是2010年的论文，当时只是讨论的Sigmoid，tanh和Softsign激活函数，解决深层神经网络梯度消失的问题，并提出了一种初始化权重weights的方法，但是对于ReLu激活函数还是失效的，下一篇再讲。
• 理解可能会有问题。

2、实验部分

• 论文先是指出了Sigmoid激励函数是不适合作为深度学习的激励函数的，因为它的均值总是大于0的，导致后面隐含层hidden layer的神经元趋于饱和
  
• 构建了含有4个隐层的神经网络，激活函数为Sigmoid,观察每一层的激活值的均值和标准差的岁训练次数的变化情况，layer1表示第一个隐含层，一次类推。
• 初始化权重,即服从均匀分布
• 如下图所示，实线表示均值mean value，垂直的条表示标准差。
  
  • 因为使用的均匀分布进行的初始化，所以前几层x的均值近似为0，所以对应Sigmoid函数的值就是0.5
  • 但是最后一层layer4的输出很快就饱和了（激活值趋于0）,训练到大100的时候才慢慢恢复正常
  • 作者给出当有5个隐含层的时候，最后一层始终处于饱和状态
  • 标准差反应的是数值的波动，可以看出后面才有了标准差的值
    
• 直观解释
  
  • 最后使用的是softmax(b+Wh)作为预测，刚开始训练的时候不能够很好的预测y的值，因此误差梯度会迫使Wh趋于0，所以会使h的值趋于0
  • h就是上一层的激活输出，所以对应的激活值很快降为0
• tanh激活函数是关于原点对称的，趋于0是没有问题的，因为梯度能够反向传回去。
  

3、初试化方法公式推导

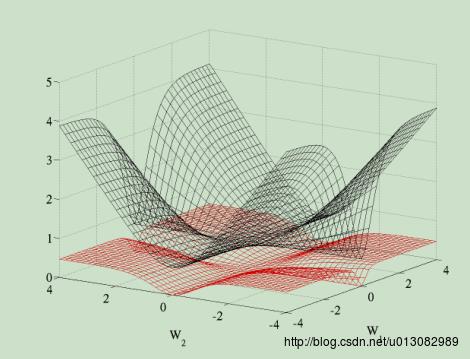
• 首先代价函数使用的是交叉熵代价函数，相比对于二次代价函数会更好，看下对比就知道了，二次代价函数较为平坦，所以使用梯度下降会比较慢。（图中W1表示第一层的权重，W2表示第二层的权重）
  
• 以tanh激活函数为例
• 符号说明
  
  • ………………………………第i层的激活值向量
  • ………………………………第i+1层的输入
  • x…………………………………输入
  • ………………………………..第i层神经元个数
  • W………………………………权重
  • Cost………………………………代价函数
• 所以第i+1层的输入：
• ，即z对应激活之后的值
• 根据BP反向传播可以得到：
  
  
  • 权重的偏导（梯度）就为：
  • 还是BP反向传播的推导，可以查看我之前给的BP反向传播的推导。
  • 它这里W是从0开始的，所以对应可能不太一致。
• tanh的导数为：
  
  • 所以：
  • 当的很小时，可以得到，
  • 这里实际上他是假设激励函数是线性的，下一篇论文中也有提到。
• 根据方差公式：可以得到：
  ，推导如下：
  
  • 
  • （式子太长，直接截图的，没用LaTex解析）
  • 因为输入的均值为0，可以得到：
  • 所以：，代入上面即可。
• 因为之前，所以可以得到：
  
• 代入到对权重w偏导（即为梯度）的方差为:
• 对于正向传播，我们希望
  
  • 对于反向传播，同样希望：
  • 两种情况可以转化为：和
    （比如第一种：， ，所以 ，第二种情况同理）
• 两式相加得：
• 最后提出了一个归一化的初始化方法,因为W服从均匀分布U[-c,c]，根据均匀分布的方差公式得：
  
  • 所以：
  • 求出，
  • 所以◆◆最终给出初始化权重的方法为：
• 这就是Xavier初始化方法