二叉树的前序遍历

Posted 2022-12-14 行路南

二叉树文章系列：

1. 二叉树的前序遍历
2. 二叉树的中序遍历
3. 二叉树的后序遍历
4. 二叉树的层序遍历
5. 二叉树的前序、中序、后序、层序遍历【解法完整版】

本文目录

• • 一、解题思路：递归
  • 二、解题思路：迭代（方法1）
  • 三、解题思路：迭代（方法2）

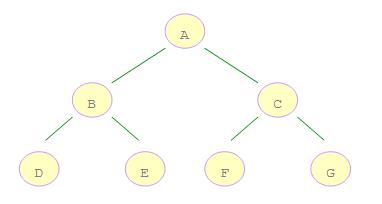
二叉树的前序遍历的记忆法则是“根左右"，即先遍历根节点，再遍历左子树节点，再遍历右子树节点。

以上图为例，前序遍历的结果是【A, B, D, E, C, F, G】

一、解题思路：递归

递归是我们实现前中后序遍历最常用的方法。

什么问题可以采用递归求解呢？

需要满足三个条件：

1. 一个问题的解可以分解为若干个子问题的解；
2. 这个问题与分解的子问题，除了数据规模不同外，求解思路相同
3. 存在递归终止条件。

那么在知道一个问题可以采用递归实现之后，如何写出递归代码呢？

关键在于能写出递归公式，找到终止条件。

在二叉树的前序遍历问题上，它的递归公式是:

preorder(node) = print node —> preorder(node->left) --> preorder(node->right)

它的终止条件是：

node 是否为空，为空则返回。

class Solution 
public:
    vector<int> preorderTraversal(TreeNode* root) 
        vector<int> res;
        preorder(res, root);
        return res;
    

    void preorder(vector<int>& res, TreeNode* root)
        
        if(!root) return;
        res.emplace_back(root->val);
        preorder(res, root->left);
        preorder(res, root->right);
    
;

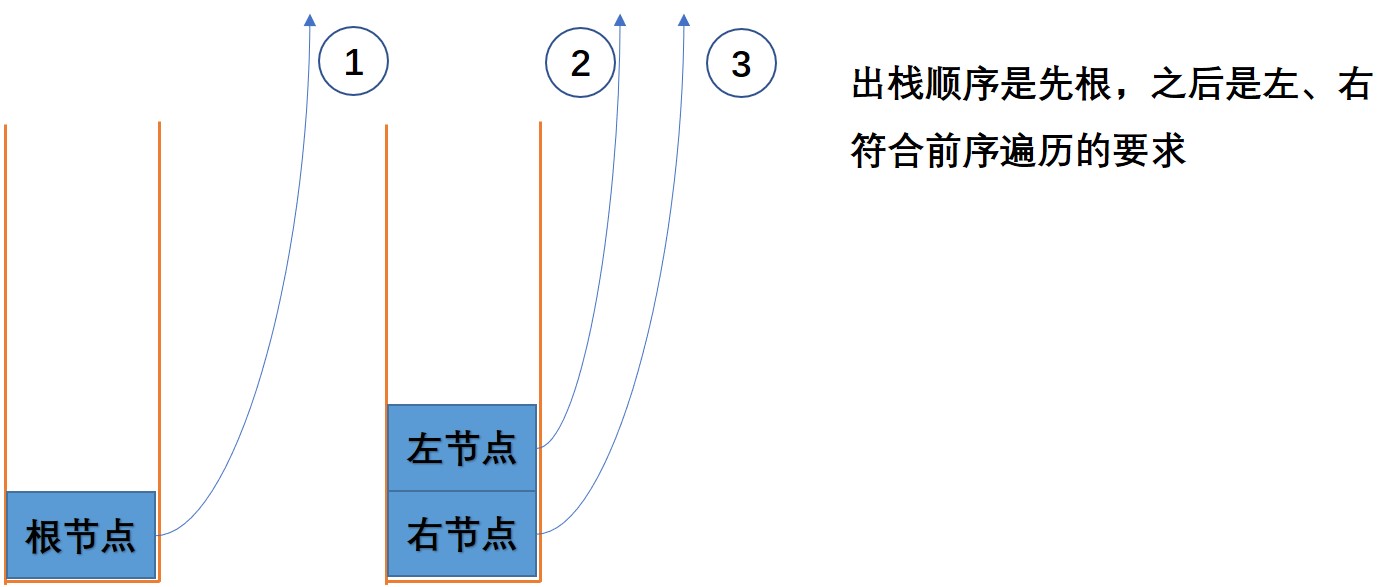
二、解题思路：迭代（方法1）

在递归方法实现过程中，它的底层是基于系统栈的结构来实现的。因此，我们可以使用栈的数据结构来辅助实现基于迭代方式的前序遍历。

具体思路为：

• 初始化栈stack，初始化输出列表res
• 根节点入栈
• while(栈不为空)，在循环体内部：
  • 栈顶元素出栈
  • 栈顶元素添加到输出列表
  • 如果栈顶元素的右子树节点不为空，将右子树节点入栈
  • 如果栈顶元素的左子树节点不为空，将左子树节点入栈
• 返回输出列表res

class Solution 
public:
    vector<int> preorderTraversal(TreeNode* root) 

        vector<int> res;
        if(!root) return res;

        stack<TreeNode*> s;
        s.push(root);

        while(!s.empty())
            TreeNode* node = s.top();
            s.pop();
            res.emplace_back(node->val);

            if(node->right) s.push(node->right);
            if(node->left) s.push(node->left);
        

        return res;


    
;

三、解题思路：迭代（方法2）

基于迭代方法的第二种思路如下：

• 初始化栈stack，初始化输出列表res
• 设置一个变量cur, 表示当前节点。并赋初始值为根节点root
• while(栈不为空 或者 当前节点cur不为空)，在循环体内部：
  • 沿着当前节点的左分支一直走，直到为空。在这个过程中将遍历的节点都入栈，同时添加到输出列表
  • 栈顶元素出栈
  • 更新当前节点cur为栈顶元素的右子树节点。
• 返回输出列表res

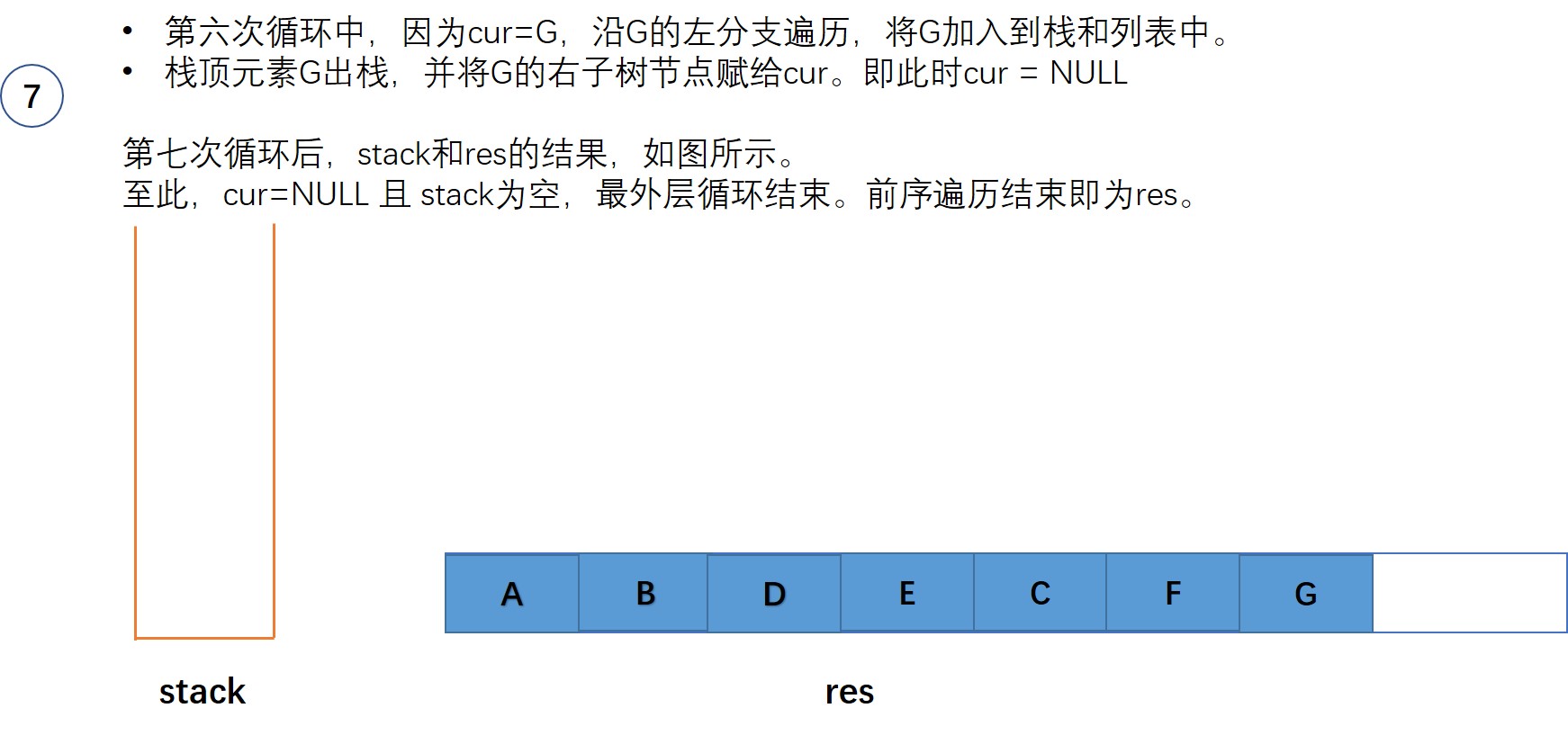
以图中的二叉树为例，来一步步来展示这个过程：

初始时，当前节点cur = root ，即节点A

class Solution 
public:
    vector<int> preorderTraversal(TreeNode* root) 

        vector<int> res;
        if(!root) return res;

        TreeNode* cur = root;
        stack<TreeNode*> s;
        while(!s.empty() || cur)
            // 沿着当前节点cur的左分支一直走到底
            while(cur)
                s.push(cur);
                res.emplace_back(cur->val);
                cur = cur->left;
            
            TreeNode* node = s.top();
            s.pop();
            cur = node->right;
        
        return res;

    
;