分类器组合方法Bootstrap, Boosting, Bagging, 随机森林

Posted 2022-12-13 Maggie张张

写在前面：机器学习的一个重要假设就是样本的分布和总体的分布是一致的。

        多分类器进行组合的目的是为了将单个分类器（也叫基分类器 base classifier）进行组合，提升对未知样本的分类准确率，（依赖于基分类器的分类性能和基分类器之间的独立性）。构建组合分类器的逻辑视图可以用以下的图表示：

                                               

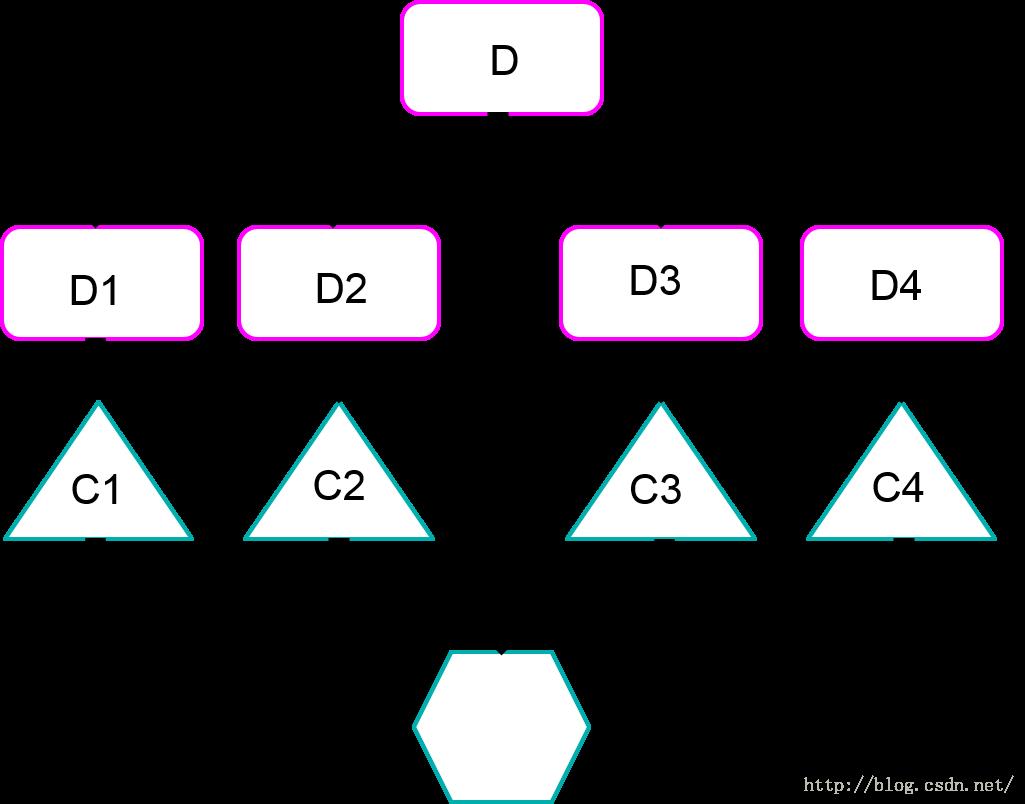
        提到组合方法（classifier combination），有很多的名字涌现，如bootstraping, boosting, adaboost, bagging, random forest 等等。那么它们之间的关系如何？用下图来理清思路：

                                   

       

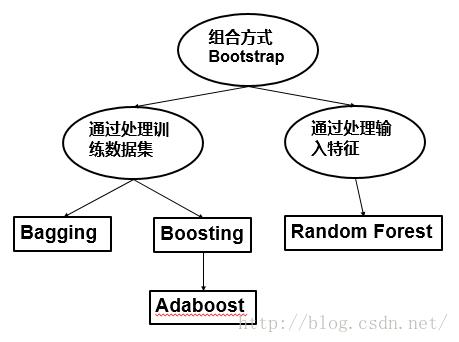
Boostrap是靴子的带子的意思，名字来源于“pull up your ownboostraps”，意思是通过拉靴子提高自己，本来的意思是不可能发生的事情，但后来发展成通过自己的努力让事情变得更好。放在组合分类器这里，意思就是通过分类器自己提高分类的性能。

Boostrap只是提供了一种组合方法的思想，就是将基分类器的训练结果进行综合分析，而其它的名称如Bagging。Boosting是对组合方法的具体演绎。

组合方法总体上可以分为两种。

第一种，通过处理训练数据集。这种方法根据某种抽样分布，通过对原始数据集进行再抽样来得到多个数据集。抽样分布决定了一个样本被选作训练的可能性大小，然后使用特定的学习算法为每个训练集建立一个分类器。Bagging袋装和Boosting提升都是这样的思想。Adaboost是Boosting当中比较出众的一个算法。

第二种，通过处理输入特征。在这种方法中，通过选择输入特征的子集来形成每个训练集。随机森林就是通过处理输入特征的组合方法，并且它的基分类器限制成了决策树。

今天我们主要着眼于Bagging、Adaboost和RF。

Bootstrap

        具体的方法是：

        （1）采用重复抽样的方法每次从n个原始样本中抽取m个样本（m自己设定）

        （2）对于m个样本计算统计量

        （3）重复步骤（1）（2）N次（N一般大于1000），这样就可以算出N个统计量

        （4）计算这N个统计量的方差

         比如说，我现在要对一些未知样本做分类，分类算法选取一种，比如SVM。我要估计的总体参数是准确率（accuracy）。对于n个原始样本，从步骤（1）开始，每次对抽取出的样本用SVM训练出一个模型，然后用这个模型对未知样本做分类，得到一个准确率。重复N次，可以得到N个准确率，然后对计算出的N个准确率做方差。

         我在考虑为什么要计算这N个统计量的方差而不是期望或者均值。方差表示的是一组数据与其平均水平的偏离程度，如果计算的方差值在一定范围之内，则表示这些数据的波动不是很大，那么他们的均值就可以用来估计总体的参数，而如果方差很大，这些样本统计量波动很大，那么总体的参数估计就不太准确？

Bagging

        是boostrap aggregation的缩写，是一种根据均匀概率分布从数据集中重复抽样（有放回的）的技术。子训练样本集的大小和原始数据集相同。在构造每一个子分类器的训练样本时，由于是对原始数据集的有放回抽样，因此同一个训练样本集中可能出现多次同一个样本数据。步骤是：

                                    

        最后对未知样本x进行分类，其结果是由单个分类器的预测结果投票表决出来的。

        举个例子，现在有一个原始数据集有10个样本，他只有一维特征x和对应的标签y，这个特征是连续的，取值从0.1到1.0，现在我们将基分类器都选择成决策树，自助样本集的数目定为5，也就是说我们要进行五组简单随机抽样。

                            

用得到的五个决策树模型对所有样本做分类，然后对五次结果做Bagging

                             

 五轮投票结果完全正确分类了原始数据集的10个样本

Boosting

         是一个迭代的过程，用来自适应的改变训练样本的分布，使得分类器聚焦在那些很难分的样本上。

        改变分布是什么意思呢？之前Bagging的过程，抽取自主样本集的时候是简单随机抽样，每个样本被抽到的概率是一样的，但是Boosting不一样，Boosting算法中给每一个样本赋予一个权值，每一轮在抽取自助样本集、训练完基分类器之后会对原始样本集做一个分类，然后跟效果比对，然后对分错的训练样本，自动的调节该样本的权值。

        权值可以用在以下方面：

       （1）可以用作抽样分布，从原始数据集中选出自助样本集（注意，Bagging抽样时样本是均匀分布的）

       （2）基分类器训练时更倾向于用用高权值的样本进行训练。

        举个例子，有10个样本，开始时简单随机抽样，每个样本被抽到的概率是一样的，都是1/10，然后第一轮结束后用得到的模型对该轮数据集中的样本分类，发现样本4被分错了，就增加它的权值，这样，第二轮抽取的时候4被抽到的概率增加了，第三轮也是一样。这样做，就可以让基分类器聚焦于难被分类的样本4，增加4被正确分类的几率。

                          

        那到底怎么根据每一轮的结果更新样本的权值，然后怎么组合基分类器的预测结果呢？有好几种用Boosting思想实现的算法，主要差别在于（1）每轮结束时如何改变样本的权值，（2）如何组合各个基分类器的预测结果，下面着重介绍Adaboost。