opengl es坐标变换2

Posted 2022-12-12 -dragon-

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了opengl es坐标变换2相关的知识，希望对你有一定的参考价值。

原文地址：http://blog.csdn.net/lyx2007825/article/details/8792475

Overview

几何数据——顶点位置，和标准向量(normal vectors),在OpenGL 管道raterization 处理过程之前可通过顶点操作(Vertex Operation)和基本组合操作改变这些数据。

Object Coordinates

对象的本地坐标系——任何变换之前的最初位置.为了变换(transformation)这些对象，可以调用glRotate(),glTranslatef(),glScalef()这些方法。

Eye Coordinates

使用GL_MODELVIEW矩阵和Object 坐标相乘所得。在OpenGL中用GL_MODELVIEW将对象对象空间(Object Space)变换到视觉空间(eye space)。GL_MODELVIEW

矩阵是模型矩阵（Model Matrix）和视觉矩阵（View Matrix）的组合 (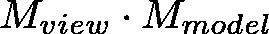)。其中，Model 变换指的是将Object Space转换到World Space

（译注：World Space值得是OpenGL中的三维空间），而View 变换是将World space变换到eye space。

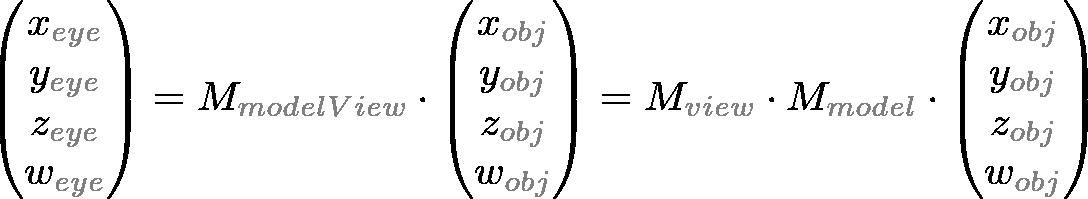
注意：在OpenGL中没有单独的camera（view） matrix。因此，为了模拟camera或者view的变换，其中的场景(3D物体和光照）必须通过和view相反的方向变换。也就是说，OpenGL总是将camera定义在(0,0,0)点，并且强制在eye space坐标系的-Z轴方向,而且不能变换。关于GL_MODELVIEW Matrix的详细资料可以查看此处:http://www.songho.ca/opengl/gl_transform.html#modelview

标准向量(Normal vectors)——从对象坐标系(Object coordinates)变换到视觉坐标系(eye coordinates)，它是用来计算光照(lighting calculation)的.注意标准向量(Normal vectors)的变换和顶点的不同。其中视觉矩阵(view matrix)是GL_MODELVIEW逆矩阵的转置矩阵和标准向量（Normal vector是）相乘所得，即：

更多关于标准向量变换(Normal Vector Transformation)的资料可连接到此处：http://www.songho.ca/opengl/gl_normaltransform.html

剪切面坐标系（Clip Coordinates）

视觉坐标系和GL_PROJECTION矩阵相乘，得到剪切面坐标系。GL_PROJECTION矩阵定义了可视的空间（截头锥体）（译注：关于什么是截头锥体，我还查了下资料，发现它是这个样子的：

，这个就是投影的效果啦）以及顶点数据如何投影到屏幕上（视角或者正交化(orthogonal)）,它被称为剪切面坐标系的原因是（x,y,z)变换之后

要和±w比较。更多关于GL_PROJECTION矩阵的资料可见:http://www.songho.ca/opengl/gl_transform.html#projection

标准化设备坐标系(NDC)

将剪切面坐标系除以w所得（关于w的讨论可见此处：,http://www.songho.ca/math/homogeneous/homogeneous.html），它被称为视角除法(perspective division)

.它更像是窗口坐标系，只是还没有转换或者缩小到屏幕像素。其中它取值范围在3个轴向从-1到1标准化了。

窗口坐标系（Window Coordinates）/屏幕坐标系(Screen Coordinates)

将标准化设备坐标系(NDC)应用于视口转换。NDC将缩小和平移以便适应屏幕的透视。窗口坐标系最终传递给OpenGL的管道处理变成了fragment。glViewPort()函数

用来定义最终图片映射的投影区域。同样，glDepthRange()用来决定窗口坐标系的z坐标。窗口坐标系由下面两个方法给出的参数计算出来

glViewPort(x,y,w,h);

glDepthRange(n,f);

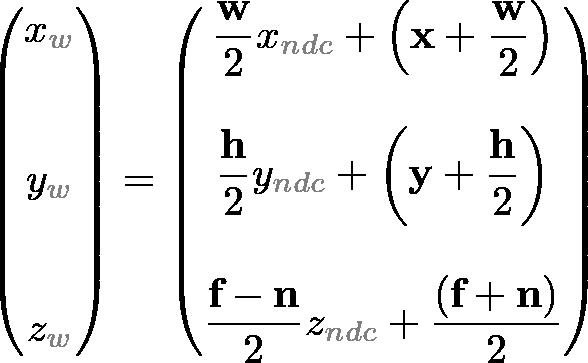
视口转换公式很简单，通过NDC和窗口坐标系的线性关系得到：

OpenGL 转换矩阵

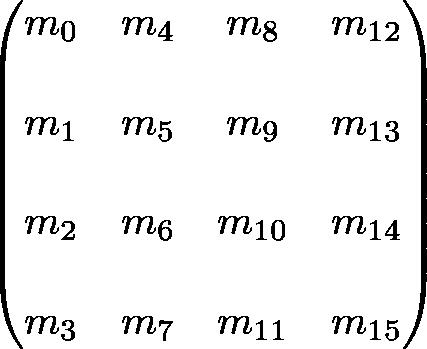
OpenGL使用4x4矩阵变换。注意，这16个元素存储在1D数组中，这些元素按列顺序排列。假如你想以行为顺序排列，你需要转置该矩阵。

OpenGL有4中不用的矩阵：GL_MODELVIEW,GL_PROJECTION,GL_TEXTURE和GL_COLOR.你可以在

代码中使用glMatrixMode()函数改变当前的类型。例如，为了选择GL_MODELVIEW矩阵，可以这样：

glMatrixMode(GL_MODELVIEW);

---------------------------------------------------------------------------------------------------------------------------------------------

Model-View 矩阵(GL_MODELVIEW)

GL_MODELVIEW矩阵在一个矩阵中包含view矩阵和model 矩阵，为了变换view(camera),你需要将整个

场景施以逆变换。gluLookAt()用来设置viewing变换。

最右边的三个矩阵元素 (m₁₂, m₁₃, m₁₄) 是用作位移变换的。m_{15元素是齐次坐标。（何为齐次坐标，参见：http://www.songho.ca/math/homogeneous/homogeneous.html），该元素是用来投影变换的。}

_{3个元素集(m₀, m₁, m₂),(m₄, m₅, m₆)和(m₈, m₉, m₁₀) 是用作欧拉变换和仿射变换，例如glRotate(),缩放glScalef().}

注意这三个元素集实际上指得是3个正交坐标系：

(m₀, m₁, m₂)： +X 轴，向左的向量(left vector)(估计是相对屏幕自己来说),默认为(1,0,0)

(m₄, m₅, m₆) : +Y轴，向上的向量(up vector),默认为(0,1,0)

(m₈, m₉, m₁₀): +Z轴，向前的向量，默认为(0,0,1).

4 columns of GL_MODELVIEW matrix

我们能够不使用OpenGL变换函数，直接构造GL_MODELVIEW矩阵。下面有一些有用的代码构建

GL_MODELVIEW矩阵

1. Angles to Axes

2. Lookat to Axes

3. Matrix4 class

注意，OpenGL在多种变换同时施加到顶点上时以相反的顺序矩阵相乘。例如，假如一个顶点先以M_A

进行变换。OpenGL首先在乘以顶点之前运用M_B x M_A 。故最后的变换出现在矩阵相乘之前，最先的变换在最后出现。

投影矩阵Projection Matrix(GL_PROJECTION)

GL_PROJECTION矩阵用来定义截锥体。该截锥体决定了那些对象或者对象的哪些部分将会被裁剪掉。同样，它也决定着3D场景怎样投影到屏幕中

（关于怎样构建投影矩阵，请查看

http://www.songho.ca/opengl/gl_projectionmatrix.html

OpenGL提供2个函数用来GL_PROJECTION变换。glFrustum()产生投影视角。glOrtho()产生正交（或者平行）投影。

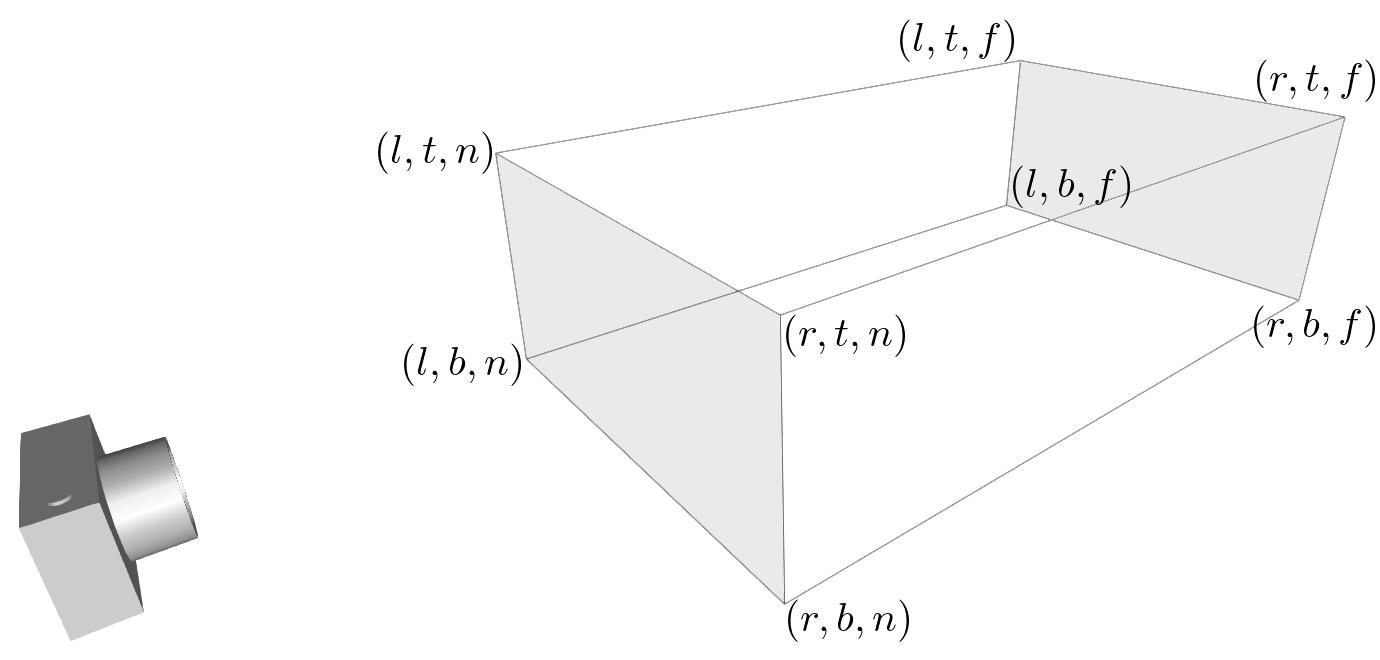
两个函数都需要6个参数决定6个剪切面：left, right, bottom, top, near, 和far 平面。截锥体的8个顶点如下所示：

OpenGL Perspective Viewing Frustum

远端平面（后面）的顶点能够简单地通过相似三角形的比率计算出来。例如，远端平面的左侧可以如下计算：

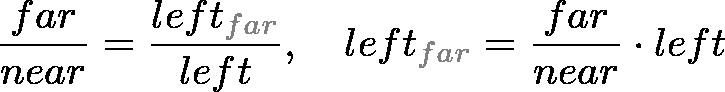
对于正交投影，ratio为1，所以远端平面的left,right,bottom和top值都与近端平面的值相同。

同样，你也可以使用gluPerspective()和gluOrtho2D()函数，但是传递更少的参数。gluPerspective()只需要4个参数：视图的垂直区域(vertical field of view(FOV)),

width/height的ratio，还有近端平面和远端平面的距离。下面代码使用gluPerspective()和glFrustum()实现同样的功能：

OpenGL正交的截锥体

OpenGL Orthographic Frustum

然而，假如你想要一个非对称的视觉空间，你可以直接使用glFrustum()。例如，

假如你想要呈现一个大的场景到2个相邻的屏幕，你可以截断截锥体变成2个不对称的截锥体(左和右)。然后，

呈现每个截锥体场景。

（这句话太不好翻译了，原位如下：

For example, if you want to render a wide scene into 2 adjoining screens, you can break down the frustum into 2 asymmetric frustums (left and right). Then, render the scene with each frustum.

An example of an asymmetric frustum