机器学习系列(23)_SVM碎碎念part6:对偶和拉格朗日乘子
Posted 寒小阳
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习系列(23)_SVM碎碎念part6:对偶和拉格朗日乘子相关的知识,希望对你有一定的参考价值。
原文地址:SVM - Understanding the math - duality-lagrange-multipliers/ by Brandon Amos
感谢参与翻译同学:@Fox && @程超 && @吕征达
时间:2018年1月。
出处:http://blog.csdn.net/han_xiaoyang/article/details/70214565
声明:版权所有,转载请联系寒小阳 (hanxiaoyang.ml@gmail.com)并注明出
1.引言
本篇是《SVM背后的数学原理》系列第6篇。今天我们将学习对偶,优化问题以及拉格朗日乘子。
如果你还没有阅读之前的文章,你可以先去阅读这篇文章:SVM碎碎念1
2.对偶
在数学优化理论中,对偶原理(the duality principle)表示一个优化问题既可以从原始问题(primal problem)的角度,也可以从对偶问题(the dual problem)的角度来处理。解决了对偶问题,就可以获得原始问题解决方案的一个下界(a lower bound)。(摘自维基百科)
如果你知道下界( lower bound)是什么,那么对偶的概念就很容易理解。
2.1 什么是下界?
如果你有一个部分有序集合
K
(有序集合指的是集合中的元素可以使用“小于或等于”关系进行比较),下界指的是集合
具体点说,从实数集
例如:
我们考虑如下 ℝ 的子集:
S=2,4,8,12
因为1小于等于2,4,8,12,那么1可以是S的下界。
-3同样符合上面的条件。
2是S中的一个元素,同样也是S的一个下界。
此外,因为2大于任何其他下界,我们给它起一个特殊的名字:下确界(infimum),即最大下界。
在上面的例子中,你可以找到无数的下界,但是下确界只有一个。
备注:同理,对于大于等于的关系,存在上界(upper-bound)和上确界(supremum)的概念。
2.2 回到对偶
现在我们知道了下界的概念,那么我们如何理解对偶的定义呢?对偶的定义表示可以将最小化问题转化为最大化问题 ,并且这个最大化问题的最大值是最小化问题的一个下界。也就是说,这个最大值小于等于最小化问题的最小值。
2.3 我们为什么关心对偶?
根据经验,有些情况下,解决对偶问题远比解决原始问题简单的多。从我们对下界已有的理解中可以得出,对于某些问题原始问题和对偶问题的结果是一样的!那什么情况下会这样?
我们看下面的图解。
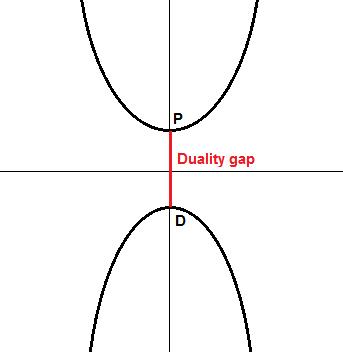
如上图所示,假设原始问题是寻找图中上半部分函数的最小值。这个最小值在
P
点。如果为上半部分的函数寻找一个对偶函数,我们可以找到图中下半部分的函数,它的最大值在
在下图中, P−D=0 ,不存在对偶间隙,我们称之为强对偶成立(strong duality holds)。
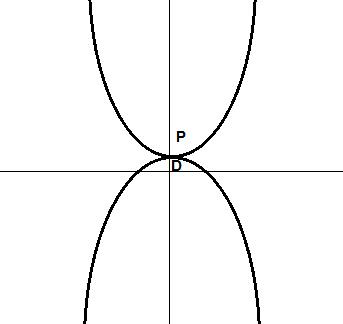
3.有约束条件的优化问题
3.1 注释
一个优化问题通常写成:
minimizexsubjecttof(x)gi(x)=0,i=1,…,phi(x)≤0,i=1,…,m
这种写法称为标准式。你应该知道还有其他多种写法。
在标准式中,
f
称为目标函数(有时也称为损失函数)。通过改变
还有
p
个定义等式约束的函数
必须遵守这些约束条件!
3.2 遵守约束是条件什么意思?
比如我们需要解决如下的优化问题:
minimizexx2
没有任何约束,找到它的最小值非常容易,当 x=0 时函数 x2 的值为0。如下图中的红色五角星:
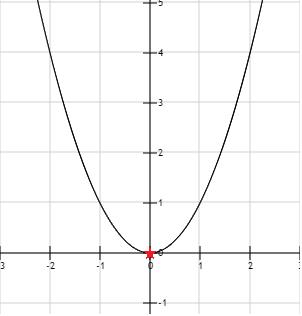
当没有任何约束是最小值是0
3.2.1 等式约束
但是,如果我们尝试添加一个等式约束呢? 例如,我们想要找到最小值,但是我们必须确保 x=1 。 这意味着我们需要解决如下的优化问题:
minimizexsubjecttox2x=1
这一次,当我们尝试 x=0 时,我们看到函数返回它的最小值。但是,我们不能说这就是优化问题的解。 事实上,这违反了约束条件 x以上是关于机器学习系列(23)_SVM碎碎念part6:对偶和拉格朗日乘子的主要内容,如果未能解决你的问题,请参考以下文章