并查集介绍及实现以及相关例题

Posted 2022-12-11 遥远的歌s

并查集的原理和使用背景

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个 单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一 个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。
比如：
某个公司的新员工有10人(这里给他们编号0，1，2，3，4，5，6，7，8，9)，其中4人(0,1,2,3)来自A城市，3人(4,5,6)来自B城市，3人(7,8,9)来自C城市，刚开始他们都不认识。当加入该公式的新职工群时，来自相同城市的人都互相认识了，他们约定一起去公司上班。
每个城市的人组成一个团队，约定每一个城市的第一号人当队长，那么可以表现如下图

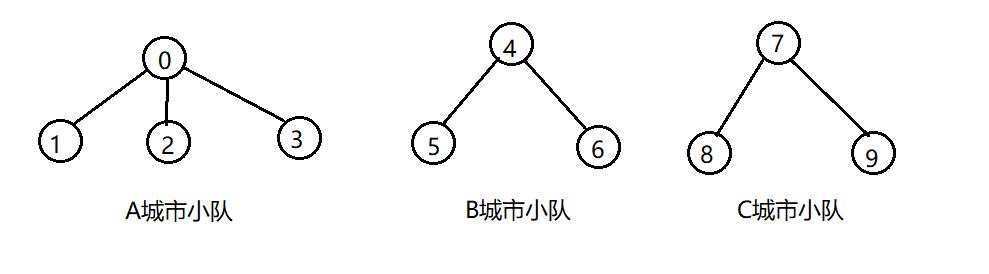
当他们一起到公司后，就熟悉了很多，就形成一个朋友圈，这里就可以用一个数组来表示。

当他们认识后，相同城市的就可以合并

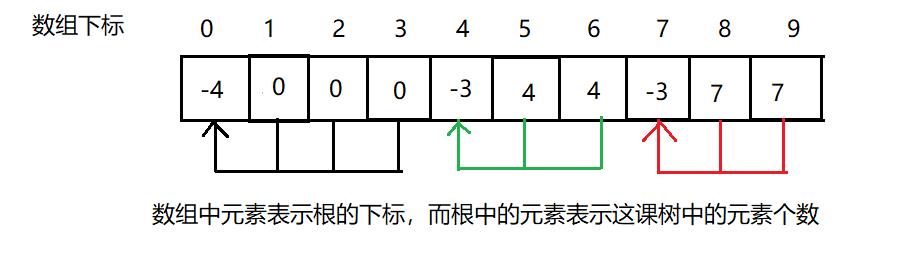
不难得出一些结论
1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素双亲在数组中的下标
当经过一段时间，A城市小队和B城市小队走到了一起，他们形成了一个朋友圈。如下图

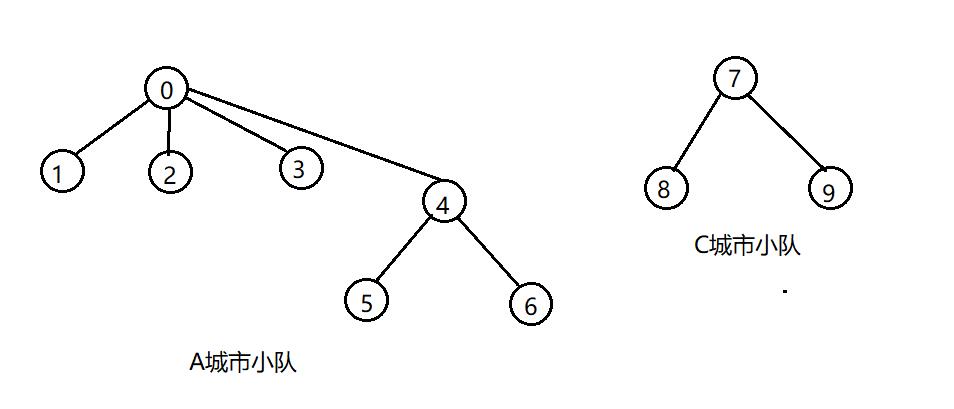
那么数组的表示如下图

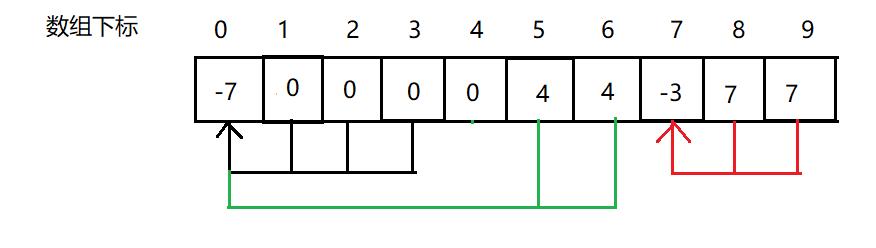
并查集实现

#include<iostream>
#include<vector>
using namespace std;
class uninfindset//并查集

public:
  uninfindset(size_t n)
  
    _v.resize(n,-1);
  
  int find_root(int x)//找根,x是下标
  
    while(_v[x] >= 0)
    
      int tmp = _v[x];
      x = tmp;
      //x = _v[x];
    
    return x;
  
  bool Union(int x1,int x2)
  
    int root1 = find_root(x1);
    int root2 = find_root(x2);
	//如果两个已经再同一个集合则返回false
    if(root1 == root2) return false;
    _v[root1]+=_v[root2];//合并
    _v[root2] = root1;//改变x2的根
    return true;
  
  //返回根的个数
  size_t count() const
  
  	size_t num = 0;
  	for(auto& ch:_v)
  	
  		if(ch<0)
  			num++;
  	
  	return num;
  
private:
  vector<int> _v;
;

例题

1.朋友圈
参考代码

class uninfindset

public:
  uninfindset(size_t n)
  
    _v.resize(n,-1);
  
  int find_root(int x)
  
    while(_v[x] >= 0)
    
      int tmp = _v[x];
      x = tmp;
    
    return x;
  
  bool Union(int x1,int x2)
  
    int root1 = find_root(x1);
    int root2 = find_root(x2);
    if(root1 == root2) return false;
    _v[root1]+=_v[root2];
    _v[root2] = root1;
    return true;
  
  size_t count() const
  
  	size_t num = 0;
  	for(auto& ch:_v)
  	
  		if(ch<0)
  			num++;
  	
  	return num;
  
private:
  vector<int> _v;
;
class Solution 
public:
    int findCircleNum(vector<vector<int>>& M) 
        uninfindset ufs(M.size());
        for(int i = 0;i<M.size();i++)
        
            for(int j = 0;j<M[i].size();j++)
            
                if(i == j) continue;//自己一样跳过不合并
                //如果等于1则表示有关系进行合并
                if(M[i][j] == 1)
                    ufs.Union(i,j);
            
        
        return ufs.count();
    
;

2.等式方程的可满足行性
参考代码

class uninfindset

public:
  uninfindset(size_t n)
  
    _v.resize(n,-1);
  
  int find_root(int x)
  
    while(_v[x] >= 0)
    
      int tmp = _v[x];
      x = tmp;
    
    return x;
  
  bool Union(int x1,int x2)
  
    int root1 = find_root(x1);
    int root2 = find_root(x2);

    if(root1 == root2) return false;
    _v[root1]+=_v[root2];
    _v[root2] = root1;
    return true;
  
  size_t count()
  
    size_t num = 0;
    for(auto& ch:_v)
    
      if(ch<0)
        num++;
    
    return num;
  
private:
  vector<int> _v;
;
class Solution 
public:
    bool equationsPossible(vector<string>& equations) 
        uninfindset ufs(26);
        //先将等于的都合并
        for(int i = 0;i<equations.size();i++)
        
            if(equations[i][1] == '=')
            
                ufs.Union(equations[i][0] - 'a',equations[i][3] - 'a');
            
        
        //查看不等于的是否再合并的集合中
        for(auto& str:equations)
        
            if(str[1] == '!')
            
                if(ufs.find_root(str[0]-'a') == ufs.find_root(str[3]-'a'))
                    return false;
            
        
        return true;
    
;