408数据结构与算法—数组和特殊矩阵的压缩存储（二十五）

Posted 2022-12-11 王同学要努力

【408数据结构与算法】—数组和特殊矩阵的压缩存储（二十五）

一、数组

• 数组：按一定格式排列起来的具有相同类型的数据元素的集合
• 一维数组：若线性表中的数据元素为非结构的简单元素，则称为一组数组
• 一维数组的逻辑结构：线性表，定长的线性表
• 声明格式：数据类型 变量名称【长度】
  
  二维数组：若一维数组中的数据元素又是一维数组结构，则称为二维数组。

声明格式：数据类型 变量名称[行数][列数]

在C语言中，一个二维数组类型也可以定义为一维数组类型（其分量类型为一维数组类型）即：

三维数组：若二维数组中的元素又是一个一维数组，则称作三维数组。

n维数组：若n-1维数组中的元素又是一个一维数组结构，则称作n维数组。

线性表结构是数组结构的一个特例，而数组结构又是线性表结构的扩展

• 数组的特点：结构固定—定义后，维数和维届不再改变。
• 数组的基本操作：除了结构的初始化和销毁之外，只有取值元素和修改元素值的操作。

二、数组的抽象数据类型定义

n维数组的抽象数据类型

😛二维数组的抽象数据类型定义

三、数组的基本操作

四、数组的顺序存储

• 数组的特点：结构固定，维数和维界不变
• 数组的基本操作：初始化，销毁，取元素、修改元素值。一般不做插入和删除操作
• 一般都是采用顺序存储结构来存储
• 注意：数组可以是多维的，但存储数据元素的内存单元地址是唯一的，因此在存储数组结构之前，需要解决将多维关系映射到一维关系的问题。

📢📢例：有数组定义:int a[5],每个元素占用4字节，假设a[0]存储在2000单元，a[3]地址是多少？

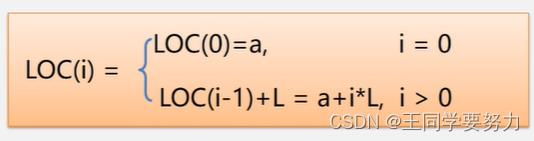
😛二维数组的存储方式

二维数组可有两种存储方式：

• 以行序为主序
• 以列序为主序
  
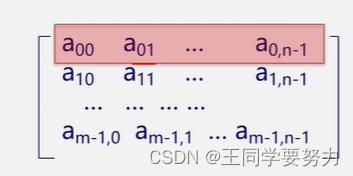
  以行序为主序
  
  以列序为主
  

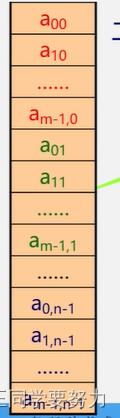
🎇二维数组的行序优先表示

以行序为主序：设数组开始存储位置LOC（0,0），存储每个元素需要L个存储单元数组元素a[i][j]的存储位置是：LOC(i,j)=LOC(0,0)+(n*i+j)*L
(n*i+j)表示a[i][j]前面所有元素的个数

🎇三维数组

按页/行/列存放，页优先的顺序存储

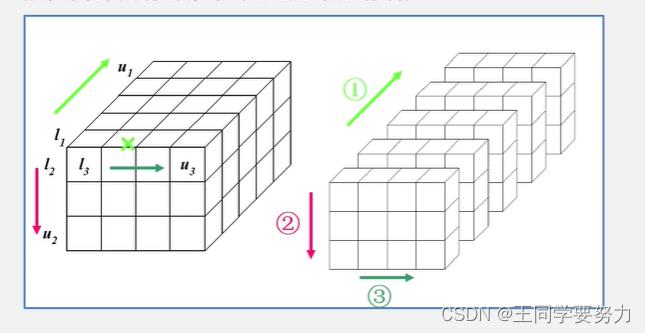
n维数组

五、特殊矩阵的压缩存储

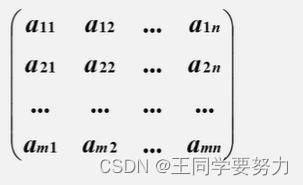
• 矩阵：一个由m*n个元素排成的m行n列的表
• 矩阵的常规存储：将矩阵描述为一个二维数组
• 矩阵的常规存储特点：可以对其元素进行随机存储 ；矩阵运算非常简单，存储的密度为1
• 不适宜常规存储的矩阵：值相同的元素很多且呈某种规律分布；零元素多
• 矩阵的压缩存储：为多个相同的为零元素只分配一个存储空间，对零元素不分配空间

1️⃣什么是压缩存储？

若多个数据元素的值相同，则只分配一个元素值的存储空间，且零元素不占存储空间

2️⃣什么样的矩阵能够压缩？

一些特殊矩阵，如对称矩阵，对角矩阵，三角矩阵，稀疏矩阵

3️⃣什么是稀疏矩阵？

矩阵中非零元素的个数较少（一般小于5%）

4️⃣对称矩阵

• 特点:在n*n的矩阵中，满足如下性质：aij=aji(1<=i,j<=n)
• 存储方法：只存储下（或者上）三角包括主对角线的数据元素，共占用n(n+1)/2个元素空间

🍑三角矩阵

特点：对角线以下（或者以上）的数据元素（不包括对角线）全部为常数C

🍑🍑对角矩阵

特点：在n*n的方阵中，所有非零元素都集中在以主对角线为中心的带状区域中，区域外的值全为0，则称为对角矩阵，常见的有三对角矩阵，五对角矩阵、七对角矩阵


存储方法：以对角线的顺序存储

稀疏矩阵存储

压缩存储原则：存各非零元的值，行列位置和矩阵的行列数

三元组顺序表

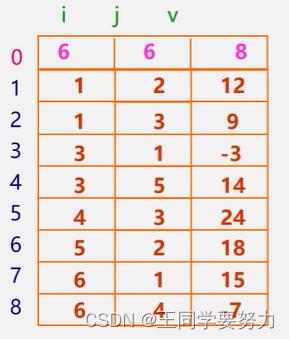
注意：为更可靠描述，通常再加一个总体信息，即：总行数、总列数、非零元素总个数

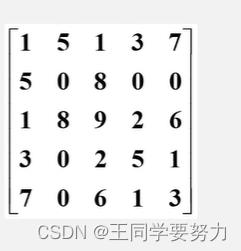
试着还原下列三元组所表示的稀疏矩阵

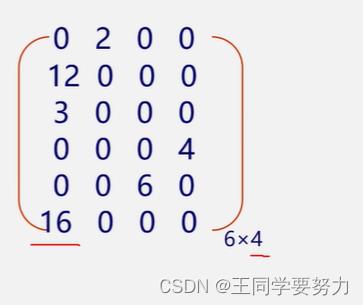
• 三元组顺序表又称有序的双下标法
• 三元组顺序表的优点：非零元素在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算
• 三元组顺序表的缺点：不能随机存储，若按行号存 取某一行中的非零元素，则需从头开始进行查找