A Busiest Computing Nodes（线段树+优先队列）

Posted 2022-12-11 jpphy0

目录

• 问题
• 分析
• 代码

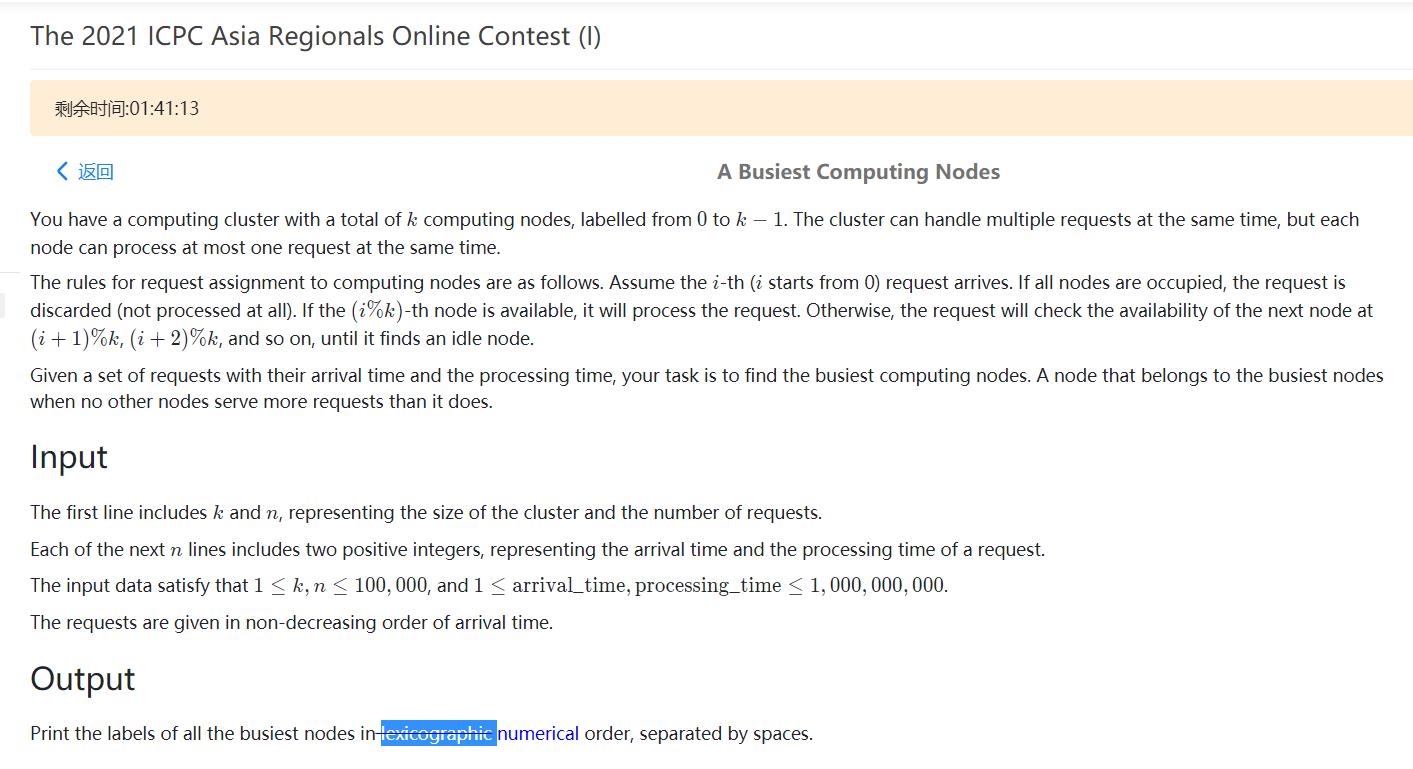
问题

Sample Input
3 5
1 5
2 2
3 3
4 3
5 3

Sample Output
1

分析

• 线段树维护空位
• 优先队列维护任务过期

代码

#include<bits/stdc++.h>
using namespace std;
const int MXN = 100010;
struct Pr
	int end, pos;
	bool operator<(Pr x)const return end > x.end;
;
priority_queue<Pr> q;
int tree[MXN<<2], k, n;
void build(int root, int l, int r)
	if(l == r)
		tree[root] = l;
		return;
	
	int mid = (l+r)>>1;
	build(root<<1, l, mid);
	build(root<<1|1, mid+1, r);
	tree[root] = min(tree[root<<1], tree[root<<1|1]);

int query(int root, int L, int R, int l, int r)
	if(l <= L && R <= r) return tree[root];
	if(R < l || L > r) return k;
	int mid = (L+R)>>1;
	return min(query(root<<1, L, mid, l, r), query(root<<1|1, mid+1, R, l, r));

void update(int root, int l, int r, int p)
	if(p > r || p < l) return; // p不在区间内
	if(l == r)
		tree[root] = tree[root] == l ? k : l;
		return;
	
	int mid = (l+r)>>1;
	update(root<<1, l, mid, p), update(root<<1|1, mid+1, r, p);
	tree[root] = min(tree[root<<1], tree[root<<1|1]);

int ask(int i)
	int p = query(1, 0, k-1, i%k, k-1);
	if(p < k) return p;
	if(i%k == 0) return k;
	p = query(1, 0, k-1, 0, i%k-1);
	return p;

int main()
	int at, pt, p, cnt[MXN], ans = 0;	
	scanf("%d%d", &k, &n);
	build(1, 0, k-1);
	for(int i = 0; i < n; ++i)
		scanf("%d%d", &at, &pt);
		while(q.size() && q.top().end <= at)
			update(1, 0, k-1, q.top().pos), q.pop();
		p = ask(i);
		if(p == k) continue;
		++cnt[p];
		update(1, 0, k-1, p);
		q.push((Pr)at+pt, p);
	
	for(int i = 0; i < k; ++i) ans = max(ans, cnt[i]);
	p = 0;
	for(int i = 0; i < k; ++i) if(cnt[i] == ans) p++;
	for(int i = 0; i < k; ++i)
		if(cnt[i] == ans)
			printf("%d", i), --p;
			if(p) printf(" ");
		
	
	return 0;