f(t)的奈奎斯特角频率为w，求f(t)cos(wt)的奈奎斯特角频率？

Posted 2023-04-25

最好能详细讲解一下！谢谢啦！

时域相加频域就取较大的那个，相乘就取和，相卷积就取较小的。这个是相乘，f(t)是w，cos(wt)的T=2pi/w. f=1/T=w/2pi. w1=2pi·f=w，奈奎斯特取两倍为2w。 相加结果为3w。

对低通信号进行采样时，依据Nyquist采样定理，采样频率至少为信号最高频率的2倍。

而对带通信号，其采样频率可以低于信号的最低频率，但必须不小于信号带宽的2倍。cos(wt)的角频率与wm的大小关系。

代数稳定性

代数稳定性判据可用来判别系统的稳定性,但它很难判别系统稳定或不稳定的程度,也很难知道系统中的各个参数对系统稳定性的影响。H. Nyquist于1932年提出的频率稳定性判据是对系统在频率域的稳定性的分析，又称为奈奎斯特( Nyquist)判据。

这个判据是由系统开环频率特性来判断闭环系统的稳定性，因此可以不求闭环系统的特征方程，就可以知道系统是否稳定，同时还可以得知系统的相对稳定性以及改善系统稳定性的途径。

参考技术A

时域相加频域就取较大的那个，相乘就取和，相卷积就取较小的。

这个是相乘，f(t)是w，cos(wt)的T=2pi/w. f=1/T=w/2pi. w1=2pi·f=w，奈奎斯特取两倍为2w。 相加结果为3w。

对低通信号进行采样时，依据Nyquist采样定理，采样频率至少为信号最高频率的2倍。

而对带通信号，其采样频率可以低于信号的最低频率，但必须不小于信号带宽的2倍。cos(wt)的角频率与wm的大小关系。

扩展资料：

代数稳定性判据可用来判别系统的稳定性,但它很难判别系统稳定或不稳定的程度,也很难知道系统中的各个参数对系统稳定性的影响。H. Nyquist于1932年提出的频率稳定性判据是对系统在频率域的稳定性的分析，又称为奈奎斯特( Nyquist)判据。

这个判据是由系统开环频率特性来判断闭环系统的稳定性，因此可以不求闭环系统的特征方程，就可以知道系统是否稳定，同时还可以得知系统的相对稳定性以及改善系统稳定性的途径。

参考资料来源：百度百科-奈奎斯特频率

参考技术B 时域相加频域就取较大的那个，相乘就取和，相卷积就取较小的。
这个是相乘，f(t)是w，cos(wt)的T=2pi/w. f=1/T=w/2pi. w1=2pi·f=w，奈奎斯特取两倍为2w。 相加结果为3w。

傅里叶变换本质

傅里叶变换的公式为

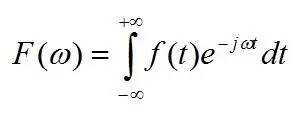
可以把傅里叶变换也成另外一种形式：

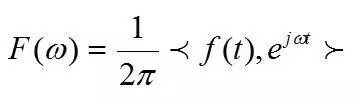
可以看出，傅里叶变换的本质是内积，三角函数是完备的正交函数集，不同频率的三角函数的之间的内积为0，只有频率相等的三角函数做内积时，才不为0。

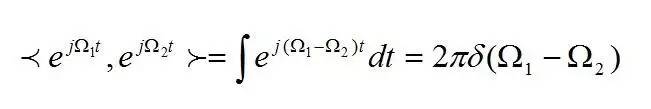
下面从公式解释下傅里叶变换的意义

因为傅里叶变换的本质是内积，所以f(t)和求内积的时候，只有f(t)中频率为w的分量才会有内积的结果，其余分量的内积为0。可以理解为f(t)在w上的投影，积分值是时间从负无穷到正无穷的积分，就是把信号每个时间在w的分量叠加起来，可以理解为f(t)在w上的投影的叠加，叠加的结果就是频率为w的分量，也就形成了频谱。

傅里叶逆变换的公式为

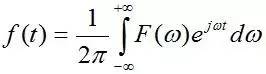
下面从公式分析下傅里叶逆变换的意义

傅里叶逆变换就是傅里叶变换的逆过程，在和求内积的时候，只有t时刻的分量内积才会有结果，其余时间分量内积结果为0，同样积分值是频率从负无穷到正无穷的积分，就是把信号在每个频率在t时刻上的分量叠加起来，叠加的结果就是f(t)在t时刻的值，这就回到了我们观察信号最初的时域。