最大熵模型
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最大熵模型相关的知识,希望对你有一定的参考价值。
参考技术A信息增益在决策树中介绍,最大熵模型之后再来更。
为了解释熵,首先要引入“信息量”这个词。直观上理解,信息量可以度量一个事件包含的信息。先给出公式,然后结合例子来理解。
信息量的定义:
例子:比如有两个事件,狗咬了人与人咬了狗,那很明显狗咬人这件事情概率大,人咬了狗这件事情概率小,所以可以通过公式来分析。log是一个单调递增的凹函数,因此公式中 越大则信息量 越小; 越小则信息量 越大。例子中,狗咬人的信息量就很小,人咬狗的信息量就很大。总而言之信息量与概率成反比,概率越低则信息量越大,概率越大信息量则越小。
有了信息量的基础,就可以用来解释熵是什么东西。简单的一句话来解释就是 “熵是信息量的期望”,先给出公式:
熵的定义:
可以看到,事件的概率乘上这个时间的信息量再求和,那就是期望的定义。熵能够反映事件的不确定性,不确定性与熵成正比关系。
联合熵实际上是表示两个变量或者多个变量熵的并集。给出公式:
多变量 联合熵的定义:
条件熵可以从引言部分中给出的Venn图中可以直观地理解,由于个人能力有限,无法用通俗的语言来解释。还是用公式来描述其含义比较准确。
条件熵的定义:
推导一波:
条件熵的两种含义:
第一种含义是说从联合熵 中减去熵 第二中含义是说熵 减去互信息 . 其中,互信息就是指两个熵的交集,接下来马上介绍互信息。
互信息的含义可以通过引言部分的Venn图理解一下,实际上就是两个熵的交集。给出公式:
互信息的定义:
特点: 互信息常用于机器学习中的特征选择和特征关联性分析。互信息刻画了两个变量之间的非线性相关性,而概率论中的相关性 用来刻画线性相关性
KL散度用来刻画两个分布之间的差异性,可参考MLPR一书中对贝叶斯的描述。有很多类似的度量两个分布P和Q的方法,如 ,这里只是mark一下,目前我还没有逐一去研究过,这里仅讨论KL散度。
为什么需要用KL散度来比较两个分布之间的差异性呢?在这个问题之前还有问题,什么是两个分布?怎么就来了两个分布?答案是实际的应用问题引出的。机器学习中有时候需要比较两个样本集的差异,按照经验比较差异那就可以用一些范数距离来求解,如用一阶范数 或者二阶范数 直接来计算不久OK了吗?当然,用范数来做有一定的道理,也是可以的,但是有一个先决条件——“两个数据集中的样本能够逐一对应”。如果不满足这个先决条件,那么用范数来度量差异性就是不合理的。实际的应用中,很难保证两个样本集中的样本能够一一对应,因此用范数距离比较差异的方法就不可行了。那么就换一种思路,我用两个样本集的分布来比较差异性,这样就回答了“两个分布怎么来的”这个问题。
再回答标题中的问题,为什么需要用KL散度来比较两个分布之间的差异性呢?答案就很简单了,KL散度只是很多种比较分布差异性的一种,我们这里讨论熵的时候就用到了相对熵,那就是KL散度。条条大路通罗马,KL散度只是其中一种方法。
假设有两个分布P和Q,我们需要求他们的相对熵,那么用公式可以表示为
相对熵的定义:
性质1:
性质2:随着 的增大,P和Q两个分布的差异会非常明显
推导一波: 为了方便进一步的推导,我们令 , 则 ; 令 则有
由于log函数是一个凹函数,因此根据凹函数的詹森不等式 ,可以对进一步推导:
其中 。通过推导可以发现
证毕!
交叉熵可以用来计算学习模型分布与训练分布之间的差异,交叉熵广泛用于逻辑回归的Sigmoid和Softmax函数中作为损失函数使用。(这句话引自 https://www.cnblogs.com/kyrieng/p/8694705.html ,感谢大佬的解读)给出公式:
交叉熵的定义
实际上交叉熵还可以这样理解:
因此,交叉熵可以看做是熵加上KL散度.
决策树中介绍(还未更)
在介绍最大熵之前,首先来明确一下事件概率的经验值和理论值
经验值:
假设有这样一个数据集 ,我们用 来表示从包含n个样本的数据集中样本 所占的比例。这个 就是我们的经验值,实际上也就是我们从数据中训练得到的值。
理论值: 理论上这个事件的概率应该如何表示呢?实际上这个问题在很早以前就学过了。就是抛硬币的例子,例如抛100次出现30次正面,抛1000次出现400次正面,抛10000次出现4800次正面....抛 次的时候出现 次正面。因此,最后逼近极限的 就是抛硬币例子中概率的理论值。在考虑我们的数据集 ,在这个例子中事件 的理论概率值就是数据集 中的样本无穷多的时候 .用公式来描述就是:
通过前面几节对熵的介绍,可以知道熵表示事件的不确定性,熵越大则不确定性越大。如果有A,B,C三件事情,通过已有数据测量发现他们发生的概率都是三分之一。那么问题来了,现在又发生了一个事件,请问到底是是A,B,C其中的哪件事情?要回答这个问题就先来看看最大熵原则是怎么说的
最大熵原则是这样一句话:承认已知数据,对未知数据无偏见。
通过这句话,我们在例子中所承认的就是“A,B,C三件事情,通过已有数据测量发现他们发生的概率都是三分之一”,对未知数据无偏见意思就是,再来一个事件我们主观地认为它可能会是哪个事件。
通过上面的例子可能会有两个问题,最大熵到底有什么用?如何应用最大熵?那么下面的例子来解释这两个问题。
插播一条李航《统计学习方法》中对最大熵原理是这样讲的“最大熵原理认为,学习概率模型时,在所有可能的概率模型中,熵最大的模型是最好的模型”
先回忆条件熵: 最大熵怎么用呢?我们可以用最大熵来确定事件的概率,然后通过概率来确定事件的归属类别。通俗地将就是可以通过对数据进行分析后进行参数估计。
用上面的条件熵可以有:
这个式子的意思就是:求解 ,使得熵 最大。实际上,这个式子就引出了最大熵模型的目标。再定义一个特征函数就构成了最大熵问题的清单。特征函数是什么呢?可以理解为数据的特征对估计结果的映射关系。接下来给出最大熵问题的清单:
接下来,有目标函数,有约束,那就可以用拉格朗日朗日乘子法求解。可以看到,这里又引入了一个经验值 ,它和理想值 相等是一个约束条件。用公式来描述:
开始构造拉格朗日函数:
对 求偏导:
令 则可以推导得到:
令 则有:
这样,我们就得到了最终所要估计的概率 .
logistic regression与最大熵模型·最大熵模型
李航·统计学习方法笔记·第6章 logistic regression与最大熵模型(2)·最大熵模型
标签(空格分隔): 机器学习教程·李航统计学习方法
注意,这里有一个前提,这里讨论的分类模型都是概率模型!
最大熵模型是另外一种机器学习模型,与逻辑斯蒂回归模型没有什么关系,只不过被安排在了一个章节讲解
最大熵原理只是一个学习的准则,利用这个准则可以从一堆概率模型中选择一个最优的
1 最大熵原理
最大熵模型是根据最大熵原理推导得到的,所以,为了推导最大熵模型,必须首先了解最大熵原理!
1.1 最大熵原理的基本内容
- 最大熵原理认为:在所有可能的概率模型中,熵最大的模型为最好的概率模型(下图中的阶段2)

这里的“所有可能的概率模型”是一个概率模型的集合,是在所有的概率模型中,根据一定的约束条件选取出来的(上图中的阶段1)
不知道能否这样理解???
比如,对应逻辑斯蒂回归模型中,它使用的用来表示分类器的模型其实就是利用逻辑斯蒂分布构造的一个概率分布,这个概率分布的形式是一定的,只不过参数待求,那么,可以将这些形式一定但参数未知的概率分布看着是“所有可能的概率模型”的集合,在这个集合中,找到熵最大的那个模型,也就实现了参数的求解综上,最大熵原理可以表述为:在满足约束条件的概率模型集合中选取熵最大的模型
那么,如何计算概率模型的熵呢? → 先讨论离散情况
对于某一个随机变量X,它的概率分布为P(X)(即PMF或者说是分布律),它的熵定义为
H(P)=−∑i=1nP(xi)logP(xi)
它表述的是随机变量X取得所有可能值 xi ( i=1,⋯,n )带来的自信息的数学期望,即表征了该信号带来的信息量!
上面的熵的取值范围是什么呢?
0⩽H(P)⩽logn
具体推导过程见《最优化理论·拉格朗日Lagrange对偶性的一个实例》所以,最大熵原理的具体内容或者说是实际使用方法为:
- 根据已有的信息(约束条件),选择适当的概率模型
- 对于那些不确定的部分,认为它们是等可能的,也就实现了最大熵的目的
- 那这个方法如何使用呢?下面给出一个实际的例子:

- 首先,根据已知条件,可以得到下面的约束:

除此信息外,不再有其他可利用信息,那么,根据最大熵原理(不确定的信息认为其为等可能),则有

- 如果接下来又添加了一个可用信息

则此时,再根据最大熵原理,可以得到
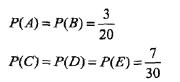
- 首先,根据已知条件,可以得到下面的约束:
1.2 最大熵原理的几何意义
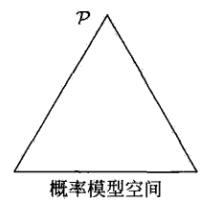
- 下图是所有可能的概率模型空间(用一个2单纯形表示),所有可能的概率空间位于三角形内部
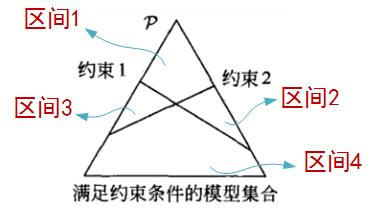
- 现在加入了两个约束条件,此时的概率空间变小了,变成了图中的5条之间的某个交集围成的区间(由于这里并没有给出两个约束的具体内容,所以这个区间还不能确定,可能是下图中的四个子区间的任何一个)
2 最大熵模型
2.1 到底应该如何表示分类模型?
- 对于分类问题,它的分类模型可以表示条件概率分布: P(Y|X)
- 例如,对于一个三分类的分类问题,这个分类模型其实就是一个离散型的条件概率分布,每个类别 Y 的概率取值都有一个模型
P(Y=i|X) ,它不是一个具体的取值,而是一个与输入的样本 X=x ( x 为一个特征向量)相关的一个函数:可以认为,该表就是要求解的分类器!!!
可能取值 类别1 类别2 类别3 分布律 P(Y=1|X) P(Y=2|X) P(Y=3|X) 通俗理解 函数 p1(x) 函数函数 p2(x) 函数 p3(x)
- 再以逻辑斯蒂回归问题的模型 P(Y|X) 为例
可能取值 Y=1 Y=0 概率 P(Y=1|X)=exp(wx)1+exp(wx) P(Y=0|X)=11+exp(wx) 通俗理解 函数 p1(x) 是 x 的函数 函数函数 p2(x) 是 x 的函数2.2 最大熵模型的约束条件
2.2.1 最大熵模型的一个总述
利用最大熵原理去求解上面所述的条件概率(应用于分类问题中),得到的分类模型就是最大熵模型
那么,应该如何做呢?
给定一个训练数据集
T=(x1,y1),(x2,y2),⋯,(xN,yN) 其中:
N 为训练集中样本个数;
xi∈X (输入空间)为输入,它其实是一个向量,代表的是输入样本的特征;
yi∈Y以上是关于最大熵模型的主要内容,如果未能解决你的问题,请参考以下文章