理论： 数论：拓展欧几里得算法及其证明

Posted 2022-12-10 sun897949163

拓展欧几里得算法

算法描述

定义1.7
.

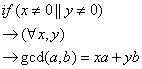
算法证明

记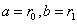,对a，b使用欧几里得定理得：
.

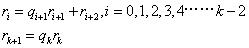
在这里我们代入 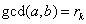，将上式改写成：

.

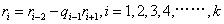
我们将上式逐一向前代回， 就将得到rk关于a和b的线性组合。
.

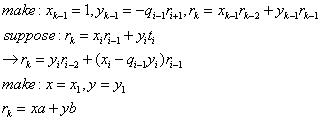
算法推论

拉梅定理：用欧几里得算法计算两个正整数的驻地啊公因子时， 所需的除法次数不会超过连个整数中较小的那个十进制数的5倍
·
拉梅定理推论：求两个正整数a，b（a>b）的最大公因子需要O（log2a3）次运算
·
拓展欧几里得推论：如果gcd(a,b) = 1， 那么a，b互素

代码实现

//     xm+yn=gcd(m,n)
long long exgcd(long long m, long long &x, long long n, long long &y)

    long long x1, y1, x0, y0;
    x0 = 1, y0 = 0;
    x1 = 0, y1 = 1;
    long long r = (m % n + n) % n;
    long long q = (m - r) / n;
    while(r)
    
        x = x0 - q * x1;   y = y0 - q * y1;
        x0 = x1;           y0 = y1;
        x1 = x;            y1 = y;
        m = n; n = r; r = m % n;
        q = (m - r) / n;
    
    return n;

主要应用

求解不定方程

求模的逆元

求解同余方程组

下文上超链接