1. Crypto 加密算法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了1. Crypto 加密算法相关的知识,希望对你有一定的参考价值。
参考技术AHash,音译为哈希,也叫散列函数、摘要算法。它是把任意长度的输入,通过散列算法变换成固定长度的输出,该输出就是散列值。
常用的哈希算法有:
MD5 信息摘要算法 (MD5 Message-Digest Algorithm),一种被广泛使用的密码散列函数,可以产生出一个128位(16字节)的散列值,用于确保信息传输完整一致。
SHA (Secure Hash Algorithm),即安全散列算法。散列算法又称杂凑算法或哈希算法,能将一定长度的消息计算出固定长度的字符串(又称消息摘要)。SHA包含5个算法,分别是SHA-1、SHA-224、SHA-256、SHA-384和SHA-512,后四者并称为SHA-2。
循环冗余校验 (Cyclic redundancy check,通称“ CRC ”)是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数,主要用来检测或校验数据传输或者保存后可能出现的错误。生成的数字在传输或者存储之前计算出来并且附加到数据后面,然后接收方进行检验确定数据是否发生变化。一般来说,循环冗余校验的值都是32位的整数。
AES ,高级加密标准(Advanced Encryption Standard),又称 Rijndael 加密法,是美国联邦政府采用的一种区块加密标准。
MAC ,消息认证码(带密钥的 Hash 函数):密码学中,通信实体双方使用的一种验证机制,保证消息数据完整性的一种工具。构造方法由 M.Bellare 提出,安全性依赖于 Hash 函数,故也称带密钥的 Hash 函数。消息认证码是基于密钥和消息摘要所获得的一个值,可用于数据源发认证和完整性校验。
PBKDF2 (Password-Based Key Derivation Function)是一个用来导出密钥的函数,常用于生成加密的密码。它的基本原理是通过一个伪随机函数(例如 HMAC 函数),把明文和一个盐值作为输入参数,然后重复进行运算,并最终产生密钥。如果重复的次数足够大,破解的成本就会变得很高。而盐值的添加也会增加“彩虹表”攻击的难度。
在需要使用 CryptoSwift 的地方将其 import 进来:
欢迎留言讨论,有错误请指出,谢谢!
Swift 开发学习交流,联系我 QQ:3500229193 入群,请备注“Swift 学习”!
非对称加密算法-RSA算法
??加密算法分为对称加密算法和非对称加密算法,其中非对称加密算法作为计算机通信安全的基石,在保证数据安全方面起着重要的作用。而相对于对称加密算法的易理解性,非对称加密算法存在一定的难度。下面通过对RSA算法的剖析,让我们更好的理解非对称加密算法的原理。
一、对称加密算法和非对称加密算法
1、对称加密算法
??对称加密算法:加密和解密都使用同样规则(密钥)的算法。
??(1)、A选择某一种规则对信息进行加密;
??(2)、B使用同一规则(逆规则)对信息进行解密;
2、非对称加密算法
??非对称加密算法:加密和解密可以使用不同的规则,只要这两种规则之间存在某种对应关系即可。
??(1)、B根据算法生成两把密钥(公钥和私钥),其中私钥是保密的,公钥是公开的,供要与B通信的其它人使用;
??(2)、A从B处获取公钥,并用它来加密;
??(3)、B得到A加密后的信息,用私钥进行解密,完成通信;
二、RSA算法的数学基础
1、互质关系
??互质又称为互素,如果两个或两个以上的整数的最大公约数是 1,则称它们为互质。比如7和10,他们最大的公约数是1,所以他们互质。8和10最大的公约数是2,所以他们不是互质。并不是只有两个质数才能形成互质。
??根据互质关系,可以得出以下结论(后面欧拉函数会用到):
- 两个不同的质数一定互质。例如,2与7、13与19。
- 一个质数,另一个不为它的倍数,这两个数互质。例如,3与10、5与 26。
- 1和任何一个自然数都互质。如1和9908。
- 2的幂和任何一个奇数都互质。如32和75、256与315。
- 相邻两个自然数互质。如15与16。
- 相邻两个奇数互质。如49与51。
2、欧拉函数
??欧拉函数指的是对正整数n,求小于或等于n的正整数中与n互质的数的数目,记作φ(n)。比如1至10中,与10形成互质关系的有1,3,7,9,所以φ(10)=4。
??欧拉函数通用公式为(除n=1外,φ(1)=1):
\\[
φ(n)=n(1-\\frac1p_1)(1-\\frac1p_2)......(1-\\frac1p_r)
\\n=p_1^k_1*p_2^k_2......p_r^k_r,其中p_1、p_2......p_r为质数
\\]
??比如φ(20)=8计算过程如下:
\\[
φ(20)=φ(2^2\\times5)=20(1-\\frac12)(1-\\frac15)=8
\\]
??欧拉函数证明如下:
- 当n=1时,φ(1) = 1
???因为1与任何数都构成互质关系,则 φ(1) = 1 。
- 当n是质数,φ(n) =n-1
???因为质数与小于它的每一个数,都构成互质关系,则φ(n) =n-1。如φ(5)=5-1=4。
当n是质数的某个次方,公式如下,其中p为质数,k为大于1的整数
\\[ φ(p^k) =p^k(1-\\frac1p) \\]
因为质数的某个次方与除与质数的倍数外都形成互质关系,而质数的倍数1 * p、2 * p、3 * p、……、p^(k-1) * p,即有p^(k-1)个,则
\\[ φ(p^k) =p^k-p^k-1=p^k(1-\\frac1p),如φ(5^3)=5^3(1-\\frac15)=100。 \\]当n可以分解成两个互质的整数之积,
\\[ φ(p_1\\timesp_2)= φ(p_1)φ(p_2) \\]
该定理用到中国剩余定理即可证明,具体过程可参考其它文档。如φ(15)=φ(3 * 5)=φ(3) φ(5) =2 * 4 =8。
根据以上推论,因为任意一个大于1的正整数,都可以写成一系列质数的积,可以推导出当n为大于1的整数时:
\\[ n=p_1^k_1p_2^k_2...p_r^k_r \\]\\[ φ(n)=φ(p_1^k_1p_2^k_2...p_r^k_r) \\]
\\[ φ(n)=φ(p_1^k_1)φ(p_2^k_2)...φ(p_r^k_r) \\]
\\[ φ(n)=p_1^k_1(1-\\frac1p_1)p_2^k_2(1-\\frac1p_2)...p_r^k_r(1-\\frac1p_r) \\]
\\[ φ(n)=p_1^k_1p_2^k_2...p_r^k_r(1-\\frac1p_1)(1-\\frac1p_2)(1-\\frac1p_r) \\]
\\[ φ(n)=n(1-\\frac1p_1)(1-\\frac1p_2)...(1-\\frac1p_r) \\]
以上即为欧拉函数的通用计算公式。
3、欧拉定理
??欧拉定理也称费马-欧拉定理,指的是:如果两个正整数a和n互质,则n的欧拉函数 φ(n) 可以让下面的等式成立。
\\[
a^φ(n)=1(mod\\ n)
\\]
??即a的φ(n)次方被n除的余数为1,或者说a的φ(n)次方减1,能被n整除。如7和5互质
\\[
7^φ(5)-1=7^4-1=2401-1=2400,可以被5整除
\\]
4、模反元素
??如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1。这时,b就叫做a的模反元素。证明如下:
\\[
a^φ(n)=a\\times a^φ(n-1) = 1(mod\\ n),其中a^φ(n-1)就是a的模反元素
\\]
三、RSA算法过程
1、生成密钥对(公钥和私钥)
随机找两个质数a和b(a和b越大越安全),并计算他们的乘积n
比如 a = 5 ,b = 11。计算他们的乘积 n = 5 * 11 = 55 ,转化为二进为 110111,该加密算法即为 6 位。本例子中是为了计算方便,所以取的数比较小,实际算法是 1024 位 或 2048 位,位数越长,算法越难被破解。
计算n的欧拉函数m = φ(n)
根据公式m = φ(55) = φ(5)φ(11) = (5-1)(11-1) = 40
随机选择一个整数e,条件是1<e<m,且e与m互质
我们随机选择e=17
计算e对于φ(n)(即m)的模反元素d
即找一个整数 d,使得 (e * d ) % m = 1。 等价于 e * d - 1 = y * m ( y 为整数) 找到 d ,实质就是对下面二元一次方程求解。 e * x - m * y = 1 。其中 e = 17,m = 40,17x - 40y = 1 这个方程可以用"扩展欧几里得算法"求解。具体求解过程略,算出一组整数解(x,y )= (33,14),即 d=33。 到此密钥对生成完毕。不同的e生成不同的d,因此可以生成多个密钥对。
??本例中公钥为(n,e) = (55 , 17),私钥为(n,d) = (55 ,33) ,仅(n,e) =(55 , 17)是公开的,其余数字均不公开。可以想像如果只有 n 和 e,如何推导出 d,目前只能靠暴力破解,位数越长,暴力破解的时间越长。
2、加密生成密文
??对明文z采用公钥(n,e)进行加密,其中明文必须转换为数字,且必须比n小。加密的公式如下:
\\[
z^e=c(mod\\ n)
\\]
??其中z为明文,n和e为公钥,c为加密后的密文,所以c可以转换为:
\\[
c=z^e \\% n
\\]
??假如明文为15,公钥(n,e) = (55 , 17),则加密后的密文c为:
\\[
c=15^17\\%55=5
\\]
3、解密生成明文
??对密文c采用公钥(n,d)进行解密,解密的公示如下:
\\[
c^d=z(mod\\ n)
\\]
??其中c为密文,n和d为私钥,z为解密后的明文,所以z可以转换为:
\\[
z=c^d\\%n
\\]
??根据上述条件,密文c为5,私钥(n,d) = (55 ,33) ,则解密后的明文z为:
\\[
z=5^33\\%55=15
\\]
四、RSA算法有效性证明
1、有效性问题
??根据上述RSA算法示例,要验证RSA算法的有效性,即验证根据加密公式:
\\[
z^e=c(mod\\ n)
\\]
??可以推导出,解密公式是有效的:
\\[
c^d=z(mod\\ n)
\\]
2、证明过程
??根据加密规则,可以推导出:
\\[
c= z^e - kn
\\]
??将上述式子代入解密公式,即求证以下式子成立:
\\[
(z^e-kn)^d = z(mod\\ n)
\\]
\\[ z^ed = z(mod\\ n) \\]
当z与n互质时
根据欧拉定理
\\[ z^φ(n) = 1(mod\\ n) \\]
则可以推出
\\[ z\\times (z^φ(n))^p=z(mod\\ n) \\]\\[ z^1+pφ(n)=z(mod\\ n) \\]
由于
\\[ ed = 1(mod\\ φ(n)) \\]\\[ ed = 1+pφ(n) \\]
所以可以推导出
\\[ z^ed = z(mod\\ n) \\]当z与n不为互质时
因为n=a*b,其中a和b都为质数。因为z和n不为互质,则z和n必定有一个公约数,由于n为两个质数a和b的乘积,则z一定为a或b的倍数,记作ka或者kb。
假定z=ka(a=kb同理)。由于b为质数,如果k为b的倍数,即k=hb,则z=hab,其中h为正整数,则推导出z大于n,但是根据条件被加密的明文必须小于n,所以可以推导出k不是b的倍数,由于b为质数,所以可以推断出k和b互质,同理,推导出ka与b互质,即z与b互质。
根据欧拉定理,可知下列式子成立:
\\[ z^φ(b)≡1(mod\\ b) \\]
可推导出:
\\[ z^φ(b)=(ka)^φ(b)=(ka)^b-1≡1(mod\\ b) \\]
对于一个数求余结果为1,那么它的n次方,求余也为1。根据这个定理,可推导出:
\\[ [(ka)^b-1]^h(a-1)≡1(mod\\ b) \\]\\[ [(ka)^b-1]^h(a-1)\\times ka≡ka(mod\\ b) \\]
\\[ (ka)^ed≡ka(mod\\ b) \\]
\\[ (ka)^ed=ka+ob \\]
由于两名等式成立,且a与b互质,可以推导出o一定为a的倍数,即0=ja,可推导出:
\\[ (ka)^ed=ka+ob=ka+jab \\]
因为z=ka,n=ab,所以可以退出:
\\[ z^ed≡z(mon\\ n) \\]
五、RSA算法的安全性
??RSA算法的安全性,是基于目前的条件下,在空间和时间上,无法对它进行有效破解。
??根据上述推导,RSA算法用到a、b、n、m、e、d六个数字。其中公钥(n,e)是公开的,其余的4个数字是保密的。其中密钥d是算法的核心。
- e*d ≡ 1 (mod m)。其中e是公开的,那就需要知道m,才能算出d。
- 根据公式φ(n)=(a-1)(b-1)=m,要计算出m,必须知道a和b。
- n=ab。只有将n因数分解,才能算出a和b。
??目前对于大数的因数分解,除了暴力破解,没有更好的途径。以现有的计算资源和能力,目前能被破解的最长RSA密钥就是768位,所以只要保证RSA密钥是1024位及以上,即可保证算法的安全性。
六、总结
1、RSA算法流程
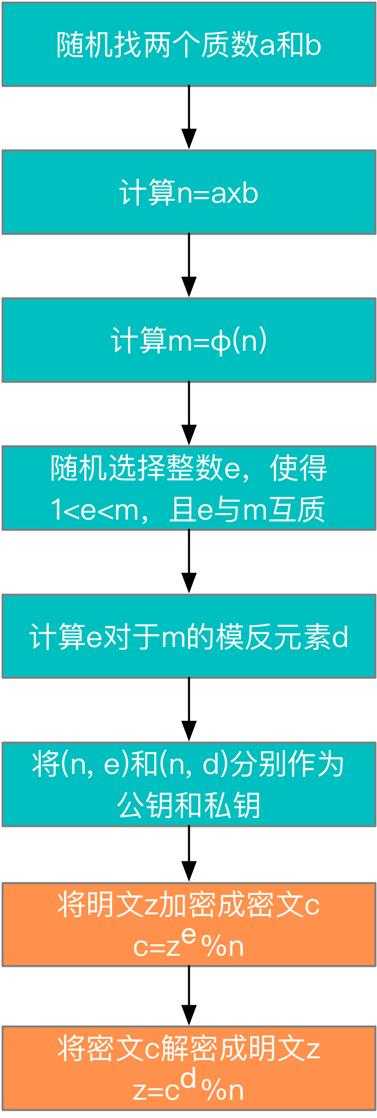
2、RSA算法安全性
??目前对于大数的因数分解,除了暴力破解,没有更好的途径。以现有的计算资源和能力,目前能被破解的最长RSA密钥就是768位,所以只要保证RSA密钥是1024位及以上,即可保证算法的安全性。
3、RSA算法应用
??在RSA算法中,公钥(n,e) 只能加密小于n的整数。对于大于n的整数,可以采用两种方法。一是把长信息分割成若干段短消息,每段分别加密;另一种是先选择一种对称性加密算法加密信息,再用RSA公钥加密对称性加密算法的密钥。
??另外,由于RSA算法性能问题,通常加解密都比较慢,所以通常和对称性加密算法一起配合使用。
以上是关于1. Crypto 加密算法的主要内容,如果未能解决你的问题,请参考以下文章