MIT 18.02 多变量微积分总结（Part II）

Posted 2022-12-09 Xurtle

Line Integrals

三种基本的曲线积分种类

line integrals with respect to arc length

求曲线长度的积分一目了然：$L=\\int_a^b ds$，其中的 $ds=\\sqrt(dx)^2+(dy)^2=\\sqrt\\left(\\fracdxdt\\right)^2+\\left(\\fracdydt\\right)^2dt$. 根据这个我们有了对弧长的线积分，它的基本形式如下：

$$\\int_C f(x,y)ds$$

从上面的曲线积分中可以看出，它的积分是一重的，而 differential 却有2个，因此我们一定需要参数化方程，从而去掉一个变量，在上面求曲线长度的积分中，变量 $x,y$ 被参数化成了一个变量 $t$。下图是我从 Paul’s Online Math Notes 截下来几种基本曲线的参数方程形式：

对于 piecewise smooth curves（比如下图） 来说，它的计算也很简单，就是把各个部分的积分累加起来，公式如下：

$$\\int_C f(x,y)ds=\\int_C_1 f(x,y)ds+\\int_C_2 f(x,y)ds+\\int_C_3 f(x,y)ds+\\int_C_4 f(x,y)ds$$

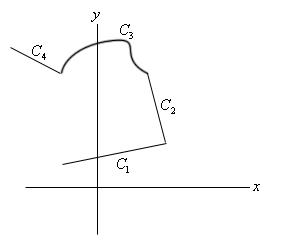
关于这种类型的曲线积分有以下2种性质：

1. Not Path-independence. 起点终点相同，但是积分路径不同，会导致不同的积分结果
2. 在同一条积分路径上，积分方向不会影响积分结果

line integrals with respect to x, y, and/or z

The line integral of f with respect to x is,

$$\\int_C f(x,y)dx$$

The line integral of f with respect to x is,

$$\\int_C f(x,y)dy$$

从上面的定义可以看出，它和对弧长的线积分唯一不同就是 differential. 上面的2种积分经常一起出现，因此通常用下面的 notation 去表示它们：

$$\\int_C P(x,y)dx+\\int_C Q(x,y)dy=\\int_C Pdx+Qdy$$

对于这种类型的积分来说，积分方向相反会导致积分的结果相反，因此得到如下3种表达：

∫Cf(x,y)dx=−∫−Cf(x,y)dx∫Cf(x,y)dy=−∫−Cf(x,y)dy∫CPdx+Qdy=−∫−CPdx+QdyMIT 18.01 单变量微积分总结

MIT 18.06 线性代数总结（Part I）

MIT 18.06 线性代数总结（Part II）

人脑天生会算微积分，并应用于精准控制奔跑，来自MIT团队

MIT 18.03 写给初学者的微积分校对活动 | ApacheCN

MIT 6.828 JOS????????????10. Lab 1 Part 3: The kernel