什么是拉普拉斯概率

Posted 2023-04-24

参考技术A 在概率论与统计学中,拉普拉斯分布是以皮埃尔-西蒙·拉普拉斯的名字命名的一种连续概率分布.由于它可以看作是两个不同位置的指数分布背靠背拼接在一起,所以它也叫作双指数分布.两个相互独立同概率分布指数随机变量之间的差别是按照指数分布的随机时间布朗运动,所以它遵循拉普拉斯分布.

贝叶斯和朴素贝叶斯是啥

目录

• 一、贝叶斯
  • 先验概率、似然概率、后验概率
  • 公式推导
• 二、为什么需要朴素贝叶斯
• 三、朴素贝叶斯是什么
  • 条件独立
  • 举例：长肌肉
  • 拉普拉斯平滑
  • 半朴素贝叶斯

一、贝叶斯

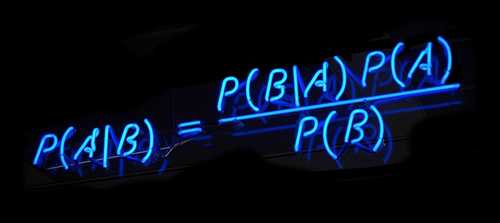
简单地说，贝叶斯就是你见到贝克汉姆，说了一句yes，研究的是这种概率事件。
开玩笑啦，贝叶斯原理是英国数学家托马斯·贝叶斯提出的，为了解决一个“逆概率”问题。
例如，如果一个男人发现了他老婆手机里暧昧短信 ，计算机他老婆出轨的概率。

现实生活中，我们很难知道事情的全貌，当不能准确预知一个事物本质的时候，但是可以依靠和事物本质相关的事件来进行判断。

先验概率、似然概率、后验概率

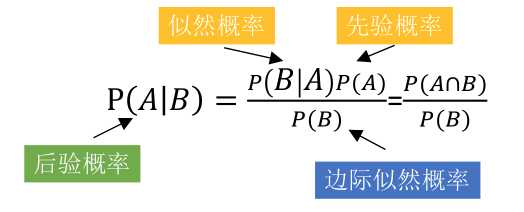
贝叶斯原理类似概率反转，通过先验概率和似然概率，推导出后验概率。
什么是先验概率、似然概率、后验概率？

再以上面出轨的例子为例，

• 先验概率：男人的老婆没有任何情况，出轨的概率
• 似然概率：男人的老婆出轨了，手机里有暧昧短信的概率
• 后验概率：男人发现老婆手机有暧昧短信，计算他老婆出轨概率

再举个例子，产品由不同的工厂ABC生产，每个工厂都有自己的次品率

• 先验概率：A厂的产品占产品总数的比例
• 似然概率：A厂的次品率
• 后验概率：已知一件产品是次品，推断这件产品来自在A厂的概率。（次品可能来自ABC中任意一个厂）

似然概率是由假设正推结果，后验概率是由结果倒推假设

公式推导

• (P(A|B))：表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。

• (P(AB))：表示事件A和事件B同时发生的概率

• (P(AB)=P(BA))，可得(P(AB)=P(BA)=P(B|A)P(A)=P(A|B)P(B))

• 通过(P(A|B))来求(P(B|A))，可得(P(B|A)=frac {P(A|B)P(B)} {P(A)})

• 分母(P(A))可以根据全概率公式分解为：(P(A)=sum_{i=1}^n P(B_i)P(A|B_i))

• 最终公式变为：(P(B|A)=frac {P(A|B)P(B)} {sum_{i=1}^n P(B_i)P(A|B_i)})

二、为什么需要朴素贝叶斯

假设训练数据的属性由n维随机向量x表示，分类结果用随机变量y表示，那x和y的统计规律就可以用联合概率分布(P(X,Y))描述，每个具体的样本((x_i,y_i))都可以通过(P(X,Y))独立同分布地产生。

贝叶斯分类器的出发点是联合概率分布，根据条件概率性质可以得到

(P(X,Y)=P(Y)?P(X∣Y)=P(X)?P(Y∣X))

• (P(Y))：每个类别出现的概率，先验概率
• (P(X|Y))：给定的类别下不同属性出现的概率，似然概率

先验概率很容易计算出来，只需要统计不同类别样本的数目即可，而似然概率受属性数目的影响，估计较为困难。
例如，每个样本包含100个属性，每个属性的取值可能有100种，那分类的每个结果，要计算的条件概率是(100^2=10000)，数量量非常庞大。因此，这时候引进了朴素贝叶斯

三、朴素贝叶斯是什么

朴素贝叶斯，加了个朴素，意思是更简单的贝叶斯。
朴素贝叶斯假定样本的不同属性满足条件独立性假设，并在此基础上应用贝叶斯定理执行分类任务。
简单地说是

对于给定的待分类项x，分析样本出现在每个类别中的后验概率，将后验概率最大的类作为x所属的类别

条件独立

要解决似然概率难以估计的问题，就需要引入条件独立性假设。
条件独立性假设保证了所有属性相互独立，互不影响，每个属性独立地对分类结果发生作用。
这样条件概率变成了属性条件概率的乘积

(P(X=x∣Y=c)=)

(P(X(1)=x(1),X(2)=x(2),?,X(n)=x(n)∣Y=c))

(prod_{j=1}^nP(X^j=x^j|Y=c))

这是朴素贝叶斯方法，有了训练数据集，先验概率(P(Y))和你似然概率(P(X|Y))就可以视为已知条件，用来求解后验概率(P(X|Y))。

给定的输入x，朴素贝叶斯分类器利用贝叶斯定理求解后验概率，并将后验概率最大的类作为输出

举例：长肌肉

肌肉是训练、睡眠、饮食多种因素组合的结果

训练	睡眠	饮食
非常好	非常好	非常好
好	好	好
一般	一般	一般
不太好	不太好	不太好
不好	不好	不好
非常不好	非常不好	非常不好

如果要计算后验概率，假设属性不独立，(6^3)就有了216组合，例如其中一种组合是{训练：好，睡眠：不好，包含：一般}，这样的组合复杂度太高了

如条件独立互不影响后，只需要考虑3个维度的结果，把最终的属性概率相乘，例如是80%(训练) * 85%(睡眠) * 90%(饮食)，算复杂度降低了几个数量级。

拉普拉斯平滑

受训练数据集规模的限制，某个属性的取值可能在训练集中从未与某个类同时出现，这就可能导致属性条件概率为0，些时直接使用朴素贝叶斯分类就会导致错误的结论。
例如：在训练集中没有样本同时具有“年龄大于 60”的属性和“发放贷款”的标签，那么当一个退休人员申请贷款时，即使他是李嘉诚，朴素贝叶斯分类器也会因为后验概率等于零拒绝。
因为训练集样本的不充分导致分类错误，不是理想的结果，为了避免这种干扰，在计算属性条件概率时需要添加一个“拉普拉斯平滑”的步骤。

拉普拉斯平滑就是计算类先验概率和属性条件概率时，在分子上添加一个较小的修正量，在分母上则添加这个修正量与分类数目的乘积，避免了零概率对分类结果的影响。

半朴素贝叶斯

属性之间可能具有相关性，而朴素贝叶斯独立假设性会影响分类性能。
半朴素贝叶斯分类器考虑了部分属性之间的依赖关系，既保留了属性之间较强的相关性，又不需要完全计算复杂的联合概率分布。
常用方法是建立独依赖关系：假设每个属性除了类别之外，最多只依赖一个其他属性。