三种形式全排列——指数型排列型组合型类型题目汇总

Posted 2022-12-09 Jocelin47

题型汇总如下：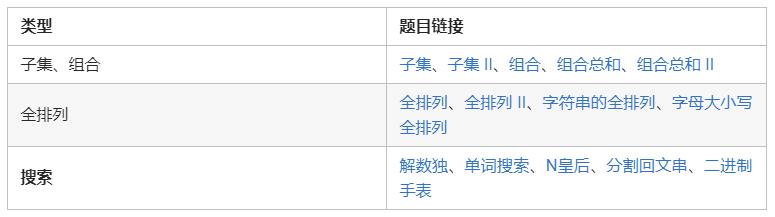

一、指数型(子集、组合问题)

1.1 递归实现指数型枚举

与leetcode78.子集是一样的
可以参考这篇链接把里面的题目都做一下，并且这一篇文章用到的子集的思路我觉得在做子集2的时候用剪枝时候的思想可以统一起来，当做模版，并且里面都是for进行遍历，剪枝的时候里面直接把剪枝的条件continue就可以了

指数型按照升序把所有中方案输出出来

#include<bits/stdc++.h>

using namespace std;

#define N 20
int n;

int st[N];
int a[N];
void dfs(int u)

    if( u == n+1 )
    
        for(int i = 1; i <=n; i++) //满足三个数的时候
        
            if(st[i]==1)  //如果我们选了这个数才把他打印出来
                cout << i << " ";
        
        cout << endl;
        return;
    
    st[u] = 0; //不选这个数我们置0
    dfs(u+1);
    st[u] = 1; //选这个数我们置1
    dfs(u+1);


int main()

    cin >> n;
    dfs(1);
    return 0;

子集[推荐写法]

这里换一种思路去写上面的问题，反正都是一直往里面添加方案，我们for遍历的时候每次从下一个数开始就可以了，得到的就是所有的方案

class Solution 
public:
    vector<vector<int>> rec;
    vector<int> path;
	vector<vector<int>> subsets(vector<int>& nums) 
		
		dfs(rec, nums, 0, path);
		return rec;
	

	void dfs(vector<vector<int>>& rec, vector<int> nums, int u, vector<int> path) 
        if(u == nums.size()+1)    //可要可不要
        	return;
		rec.push_back(path);
		for (int i = u; i < nums.size(); i++) 
			path.push_back(nums[i]);
			dfs(rec, nums, i + 1, path);
			path.pop_back();
		
	
;

1.2 子集II 这一题可以跟全排列2进行比较，里面的退出剪枝条件是一样的

class Solution 
public:
    vector<vector<int>> rec;
    vector<int> path;
    int st[20] = 0;
    vector<vector<int>> subsetsWithDup(vector<int>& nums) 
        sort(nums.begin(),nums.end());
        dfs(0,nums);
        return rec;
    
    void dfs(int u,vector<int>& nums)
    
        int n = nums.size();
        if( u == n)
        
            rec.push_back(path);
            return;
        
        //不选
        dfs(u+1,nums);

        //选
        if( u > 0 && nums[u] == nums[u-1] && st[u-1] == 0)
            return;
        if( st[u]==0 )
        // if( st[u]==0 && (u==0 || nums[u] != nums[u-1] || st[u-1] == 1))
        
            st[u] = 1;
            path.push_back(nums[u]);
            
            dfs(u+1,nums);
            path.pop_back();
            st[u] = 0;
        
    
;

实现方法二：按照上面子集的方法去写，然后剪枝跟下面的全排列2的方法一样 [推荐写法]

class Solution 
public:
    vector<vector<int>> rec;
    vector<int> path;
    bool st[11] = 0;
	vector<vector<int>> subsetsWithDup(vector<int>& nums) 
        sort(nums.begin(),nums.end());
		dfs(rec, nums, 0,st);
		return rec;
	

	void dfs(vector<vector<int>>& rec, vector<int> nums, int u,bool st[]) 
        if(u == nums.size()+1)    
            return;
		rec.push_back(path);
		for (int i = u; i < nums.size(); i++) 
            if(i > 0 && nums[i] == nums[i-1] && st[i-1] == 0) //不是第一个数，且不重复的数
                continue;
            st[i] = 1;
			path.push_back(nums[i]);
			dfs(rec, nums, i + 1,st);
            st[i] = 0;
			path.pop_back();
		
		
	
;

二、排列型

2.1 94. 递归实现排列型枚举

全排列则需要多加一个for遍历所有的开始情况，而不是选或不选，而是标记状态选没选过。

#include<iostream>

using namespace std;

int n;
#define N 10
int st[N];
int a[N];
void dfs(int u)

    if( u == n + 1)
    
        for(int i = 1; i <= n; i++)
        
            cout << a[i] << " ";
        
        cout << endl;
        return;
    
    
    for(int i = 1;i <=n;i++) //枚举所有的可能
    
        if(st[i] == 0)
        
            a[u] = i;
            st[i] = 1;
            dfs(u+1);
            st[i] = 0;
            
        
        
    



int main()

    cin >> n;
    dfs(1);
    return 0;

用vector实现更容易理解 [推荐写法]

#include<iostream>
#include<vector>
using namespace std;

#define N 1000
int n;
vector<int>res;
bool st[N];

void dfs(int u)
    
     if(res.size()==n)
     
         for(auto a: res)
            cout << a << ' ';
         cout << endl;
         return;
     
     
     for(int i = 1;i <= n; i++ )
     
          if(st[i]==0)
          
              res.push_back(i);
              st[i] = 1;
              dfs(u+1);
              res.pop_back();
              st[i] = 0;
          
          
     


int main()

    cin >> n; 
    dfs(1);
    return 0;

2.2 46. 全排列

class Solution 
public:
    vector<vector<int>> res;
    vector<int> path;
    int st[1000] = 0;
    vector<vector<int>> permute(vector<int>& nums) 
        int n = nums.size();
        dfs(1,n,nums);
        return res;
    
    void dfs(int u,int n,vector<int>& nums)
    
        if( path.size() == n)
        
            res.push_back(path);
            return;
        

        for(int i = 0; i < n;i++)
        
            if( st[i] == 0)
            
                st[i] = 1;
                path.push_back(nums[i]);
                dfs(u+1,n,nums);
                st[i] = 0;
                path.pop_back();
            
        

    
;

2.3 全排列2

class Solution 
public:
    vector<vector<int>> res;
    vector<int> path;
    int st[1000] = 0;
    vector<vector<int>> permuteUnique(vector<int>& nums) 
        int n = nums.size();
        if(n==0)
            return res;
        sort(nums.begin(),nums.end());
        dfs(0,n,nums);
        return res;
    
    void dfs(int u,int n,vector<int>& nums)
    
        if( path.size() == n)
        
            res.push_back(path);
            return;
        

        for(int i = 0; i < n;i++)
        
            if( i>0 && nums[i] ==  nums[i-1] && st[i-1]==0) //如何筛选重复出现的数字，
            //比如 1 1如果前面 st[i-1] =0,第一个1没有用过，而第二个1就不可以再用了，这样就可以得到筛掉重复出现的数字。
            //如果第一个用了第二个就可以再用一次。
                continue;
            if( st[i] == 0)
            
                st[i] = 1;
                path.push_back(nums[i]);
                dfs(u+1,n,nums);
                st[i] = 0;
                path.pop_back();
            
        

    
;

2.4 字符串的全排列

2.5 784. 字母大小写全排列

跟子集的写法又有点像了

class Solution 
public:
    vector<string> rec;
    string path;
    vector<string> letterCasePermutation(string s) 
        dfs(0,s);    
        return rec;
    
    void dfs(int u,string s)
    
        rec.push_back(s);

        for(int i = u; i < s.size();i++)
        
            if( s[i] <= 'z' && s[i] >='a')
            
                s[i] -= 32;
                dfs(i+1,s);
                s[i] += 32;
            
            else if(  s[i] <= 'Z' && s[i] >='A' )
            
                s[i] += 32;
                dfs(i+1,s);
                s[i] -= 32;
            
        
    
    
;

三、组合型

3.1 93. 递归实现组合型枚举

实现思路1：用start索引

#include<iostream>

using namespace std;

#define N 1000
int n,m;
int st[N];
void dfs(int u, int start)
                                         //剩余可选的数
    if( u + (n - start) < m ) //已经选的数u + (总数n - 起始的start)
        return;
    if( u == m + 1)
    
        for(int i =1;i<=m;i++)
        
            cout << st[i] << " ";
        
        cout << endl;
        return;
    
    
    for(int i = start; i <=n; i++)
    
        st[u] = i;
        dfs(u + 1,i + 1); //下一个开始的点为i+1
        st[u] = 0;
    
    


int main()

    cin >> n >> m; 
    dfs(1,1);
    return 0;

实现思路二：更容易理解 [推荐写法]

#include<iostream>
#include<vector>
using namespace std;

#define N 1000
int n,m;
vector<int>res;

void dfs(int u)
     if(res.size()==m)
     
         for(auto a: res)
            cout << a << ' ';
         cout << endl;
         return;
     
     for(int i = u;i <= n; i++ )
     
          res.push_back(i);
          dfs(i+1);
          res.p
以上是关于三种形式全排列——指数型排列型组合型类型题目汇总的主要内容，如果未能解决你的问题，请参考以下文章
 
 hdu 1521 排列组合 —— 指数型生成函数
 递归实现指数型 / 组合型 / 排列型枚举
 递归实现组合型指数型排列型 枚举
 排列组合 HDU - 1521 -指数型母函数
 hdu1521 排列组合(指数型母函数)
 HDU 1521 排列组合 指数型母函数