超级干货：BPSK/QPSK数字调制系统误码率MATLAB仿真

Posted 2022-12-09 爱吃猫咪的花酱

本文旨在通过简单实例来对基于MATLAB的数字调制解调系统仿真进行一个较为全面的介绍，并加深对一些基础知识的理解。且有详细解释大多数人在进行数字调制MATLAB仿真时遇到的大部分问题。

数字调制的概念

数字调制是把数字信号即二进制比特或一定长度的比特串变换为连续信号波形，进而在连续信道中传输的过程。其向信道编译码器提供了一条透明的离散编码信道。大多数情况下，我们将调制过程分成以下几个子过程：

1. 比特（串）到星座图中信号的映射（mapping）。（离散信号）
2. 离散信号（可以为一维实信号或二维复信号）向波形（waveform）的转换。（连续基带信号）
3. 基带波形与载波相乘变换到射频。（可能先到中频再上变频到射频）

所以一般情况下，不进行特殊说明，调制指的是过程1，即映射。映射包含了两层含义：

• 星座图
• 星座图中各信号点对应的比特串

后者也称为标识（labeling）方式，当星座图确定时，映射指的也就是标识，不过以标识称之更加准确。$M$阶调制存在 $M!$ 种可能的标识方案，标识方案对系统的性能有很大的影响。最常见的标识方式为 Gray 标识，其特点是星座图中邻近的两个信号，其标识仅有一位不同，这样当误符号率一定时，误比特率（BER）最小。

BPSK与QPSK仿真实例

星座图与标识方式

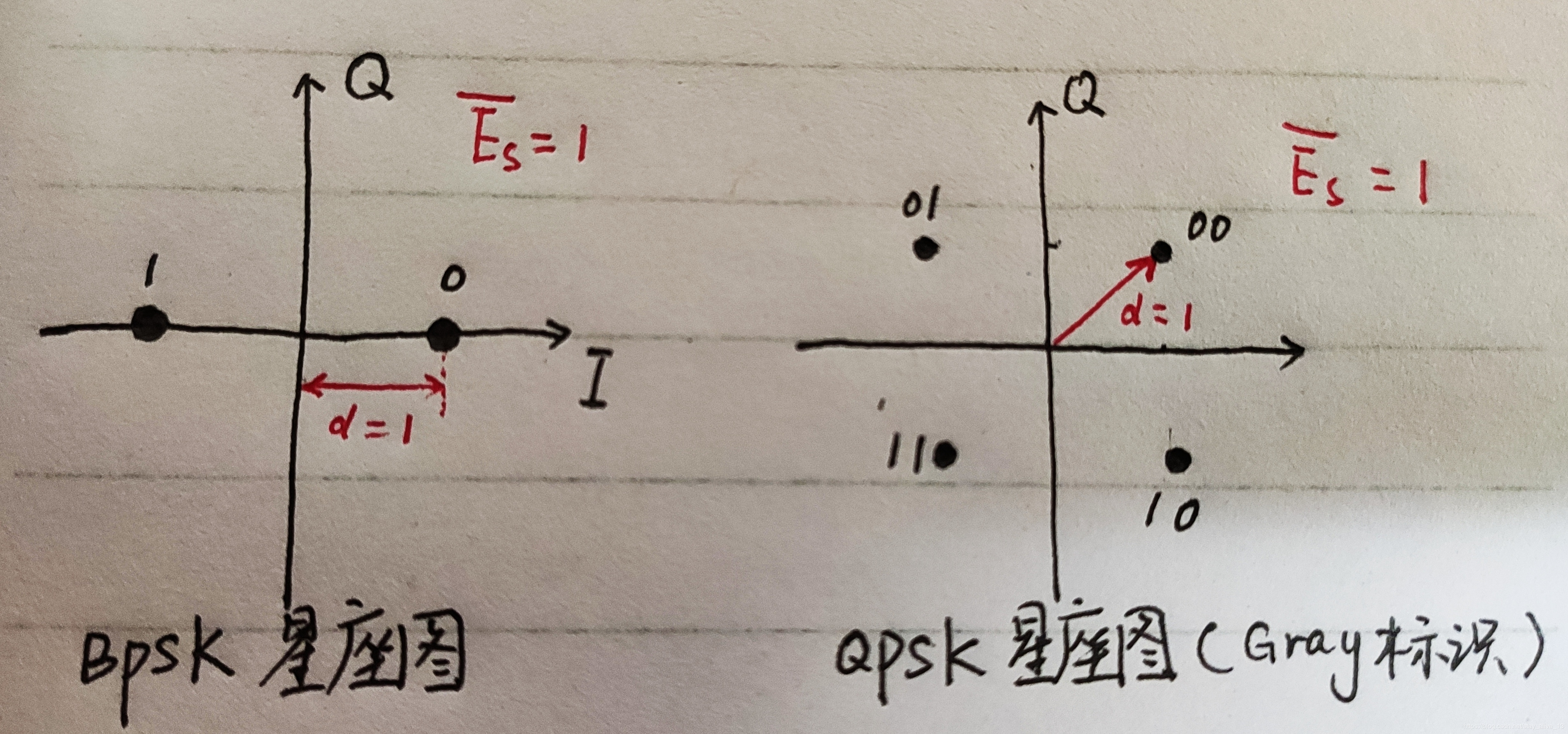
上述星座图并不是唯一的，也可以有任意的旋转角度。

对于BPSK调制，比特到信号的映射关系$s=\mu (b)$可以表示为：
$$s=1-2b,b=0,1$$
对于QPSK，映射$s=\mu (b_1,b_0)$可以表示为：
$$s=\frac{(1-2b_0)+j(1-2b_1)}{\sqrt{2}}$$
利用上面两个映射关系，就可以实现自己调制，而不用使用MATLAB中的函数或工具箱中的函数（或Object）。

调制模块代码

以下代码完成调制功能：

%% BPSK Modulation
frameLength = 10000;
b = randi([0, 1], frameLength, 1);
s_bpsk = 1 - 2 * b;

%% QPSK Modulation

% method 1
frameLength = 10000; % bits per data frame
b = randi([0, 1], frameLength, 1);
qpskMod = comm.QPSKModulator('BitInput', true, 'PhaseOffset', pi/4, 'SymbolMapping', 'Gray');
s_qpsk_1 = qpskMod(b);

% method 2
frameLength = 10000; % bits per data frame
M = 4; % Modulation Order
symLength = frameLength / M; % symbols per data frame
sym = randi([0, M-1], symLength, 1);
s_qpsk_2 = pskmod(sym, M, pi/4, 'gray');

注意：BPSK调制尽量不要使用MATLAB中自带函数。
如pskmod函数和comm.BPSKModulator，你可以自行尝试一下，调制的结果是复数形式，虽然虚部为0。但是当你使用awgn函数加噪声时，该函数会给两个维度（实部和虚部）都加上噪声，而不是只给一个维度上加，这必然导致实际的噪声功率为设想的一半。换句话说，仿真结果相比理论情况有3dB的增益，不过这是错误的。

添加AWGN噪声

$\frac{E_b}{N_o},\frac{E_s}{N_o},SNR$的辨析

基本概念

1. $E_b$表示信息比特能量， $E_s$表示符号能量

   在一个星座图中，每一个符号$s$都有其符号能量$E_s=|s{|}^2$,该星座图的平均符号能量为：
   $${\overline{E}}_s=\sum _{m=0}^{M-1}|s_m{|}^2$$

2. $N_o$表示高斯白噪声的单边功率谱密度

3. $SNR$表示每一个采样时刻信号功率与噪声功率的比值
   $$SNR=\frac{{\sigma }_s^2}{{\sigma }_n^2}$$

相互之间的关系

1. $E_b$与$E_s$之间的关系
   $$E_b=\frac{E_s}{information\_bits\_per\_symbol}$$

注意此处为每个符号所携带的信息比特数，因为在存在信道编码的场景下，符号所携带的还有冗余校验比特。对于采用$M$阶调制，以及码率为$R$的信道编码的情况，上面公式中的$information\_bits\_per\_symbol={\log }_2^M\ast R$

2. $N_o$与${\sigma }_n^2$的关系
   • 对于实信号，即一维调制（BPSK，PAM）
     $$N_o=2{\sigma }_n^2$$
   • 对于复信号，即IQ调制
     $$N_o={\sigma }_n^2$$
     $${\sigma }_{nI}^2={\sigma }_{nQ}^2=\frac{{\sigma }_n^2}{2}=\frac{N_o}{2}$$
     综上，可知对任意维度，都有
     $$N_o=2{\sigma }^2$$
     推导过程在附录中给出。
3. E s E_s Es以上是关于超级干货：BPSK/QPSK数字调制系统误码率MATLAB仿真的主要内容，如果未能解决你的问题，请参考以下文章

   调制识别基于高阶累积量的调制方式识别算法matlab仿真，课题识别BPSK, QPSK, 16QAM, 64QAM

   通信算法之三十三：5G NR LDPC仿真链路

   各类数字调制系统仿真与误码率分析ASK,FSK,PSK

   频带传输数字频带传输系统之不同调制方式的误码率与频谱特性总结

   数字调制系统的误码率matlab仿真,对比ASK,FSK和MDPSK

   用matlab viterbi算法怎么求传输