[动态规划与回溯算法] 01背包

Posted 2022-12-08 一个正直的男孩

01背包问题

题目描述：

大白话：有n个商品且每个商品的价格和重量都不一样，现在有一个m空间大小的包，你在n个商品中选取并使包中物品价格和为最大值

思路：

小时候不是有一篇课文叫小猴子下山，现在博主自编后续(如有雷同纯属巧合)

故事中所会遇到的物品

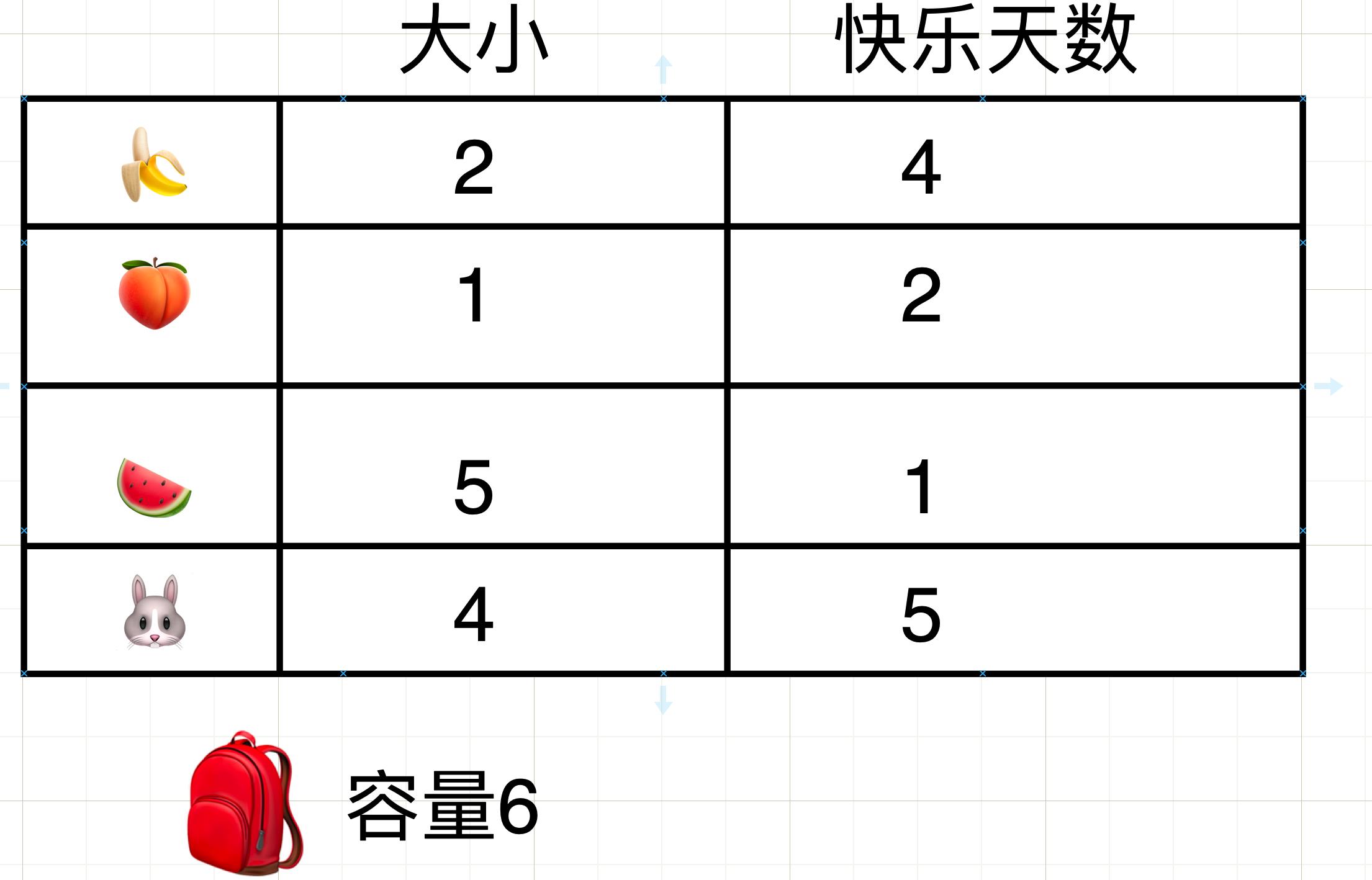
回到家的小猴子很不甘心就发明了一个时光机，这次他带着一个背包穿越时空，这次他依旧是原路程下山他先看到了 🍌他放入的包里，继续下山他看到了🍑他看了下包里空间又把桃子放入包中，继续下山这次看到了🍉看了看包里的容量这个时候小猴子需要进行一个抉择是装西瓜还是不装西瓜

1. 装🍉（丢弃包中的🍌）
2. 不装🍉

显然选择🍉，大小太大了，让小猴子快乐的天数也不多所以他选择了2不装，继续下山，这次他看到了🐰且有上次的经验,小猴子顺利捉到了🐰，但是又陷入了抉择

1. 装🐰（丢弃🍑）
2. 不装
   
   

这一次显然是丢弃了桃子带着兔子下了山，且现在小猴子包里的物品可以让小猴子快乐天数最多的

状态的定义：

可以如小猴子例子中一样，把物品抽象成状态，当全部物品都遇那么这个包里面都的价值也就是最大化的(如上述小猴子)


二（没错这里需要俩个状态定义）
他的背包也是在动态变化，就类似自己书包一样把每个区域划分出来，背包也类似对此划分出来（或许可以说背包是在动态增长的max为小猴子中的6）

那么我们如何在程序中定义一个背包呢？

动归这一类问题一般是用一个数组来存储问题的解，那么我们是用什么数组来存储解呢？


你看物品有 商品 与 价格，是俩独立的东西，所以我们用一个二维数组来存解（i,j）,i==价格，j==空间（抽象的状态后面有图解）

状态的初始化：

当小猴子刚下山的时候又一段路是空的所以说明这个包也是空的
也就是 [0][j个元素]==0，且有可能上来的物品就比背包大所以 [i][0]==0

转移方程

在故事中小猴子装东西又俩种情况

1. 直接装
2. 空间空间不够丢弃东西装装价格高的（快乐天数==商品价格）
3. 太大了装不下（上次背包所剩下的物品）
   
   转移方程就是 f(i,j)=max(f[i-1][j-1],f[i-1][j-A[i-1]]+V[i-1])
   有疑惑很正常，其实你没有吧这个背包抽象好（或许我描述的不够清楚），下面就是背包的实体化

图解整个过程：

代码：

int backPackII(int m, vector<int> &A, vector<int> &V)
    
        // write your code here

        //初始化容器
       vector<vector<int>>result;
        vector<int>d1;
        d1.resize(m+1,0);
        result.resize(A.size()+1,d1);

        //状态初始化
            //result[0][j]==0
            //result[i][0]==0


         //状态的定义与转移方程
         int i;
         for(i=1;i<=A.size();i++)//物品个数
          
              for(int j =1;j<=m;j++)//背包的空间
              
                  //方程1：result[i-1][j-A[i-1]]+V[i-1],物品大小可以放入
                  //方程2: result[i-1][j] 物体的大小比背包大
                  if(A[i-1]<=j)
                  
                      result[i][j]=max(result[i-1][j],result[i-1][j-A[i-1]]+V[i-1]);//体积过关了，但是他的价格一定要是最高的
                  
                  else
                  
                      result[i][j]=result[i-1][j];//体积太大放不下那么热背包里面还是只有上次所剩的物品
                  

              
          
            return result[i-1][m];//返回最优解
    

题目链接

唠唠家常

小猴子下山的故事原本的寓意是做事要一心一意一篇小学的课文我陷入了沉思，我现在就如这只小猴子做着一件事想着另一件事