递归：数组分治求和

Posted 2022-12-08 我家大宝最可爱

数组分治求和

数组求和的递归是我自己瞎想的，主要是想要使用归并的思想，我们依然把原问题划分为子问题，进而缩小问题规模。但是这里我们需要调用两次子问题，我们把数组分为两个部分，然后分别求解出左边数组的和，右边数组的和，之后将其相加就是总的和

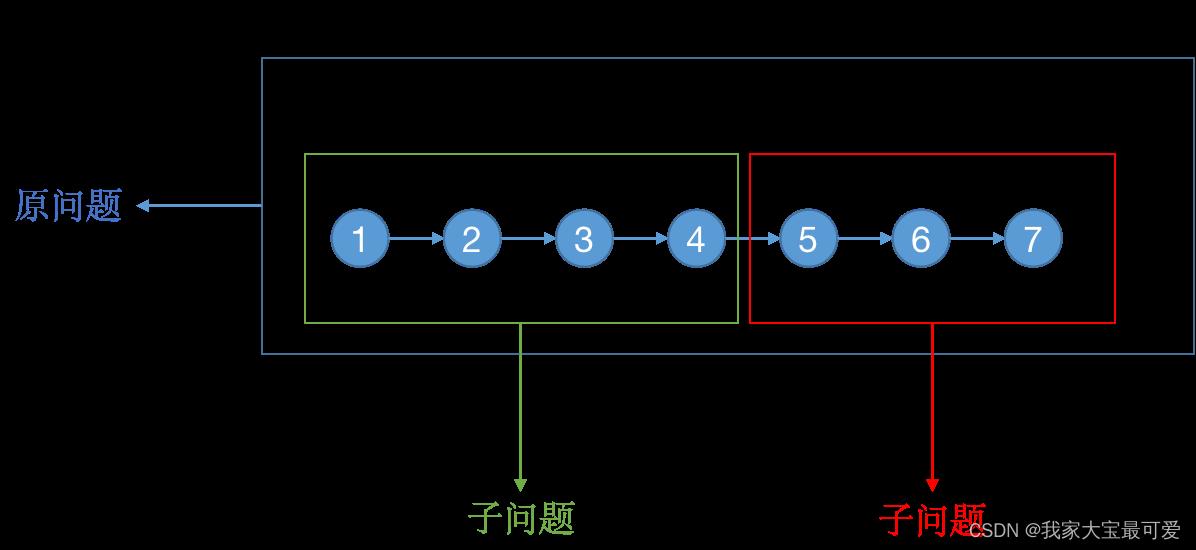
这个问题也很好的说明了递归的一个特点，那就是缩小问题规模，子问题与原问题是等价的，我们求解出子问题之后，需要再进行一些逻辑操作。现在突然想到一个问题，子问题与原问题等价吗？

1. 逻辑上肯定是相同的，只是问题规模缩小了。
2. 那些逻辑操作则是解决问题的

arr = [-1,2,3,4,5,6]

def mergeAdd(arr, l,r):
    if l >= r:
        return arr[l]
    
    m = (l + r) // 2

    lsum = mergeAdd(arr, l, m)
    rsum = mergeAdd(arr, m+1, r)

    return lsum + rsum

res = mergeAdd(arr,0,len(arr)-1)
print(res)

1. 终止条件，当左游标大于等于右游标的时候，说明只有一个元素了，此时直接返回值即可
2. 子问题和重复逻辑，原来求解的是0到len(arr)-1所有元素的和，现在求解成子问题0到m和子问题m+1到len(arr)-1和，调用了两次子问题，之后将求解的和相加即是总的和