通学智能合约系列（十五）--函数修改器modifier

Posted 2022-12-08 通学技术

写在前面

大家好，真的是我，我又来啦。通学技术，学通技术，欢迎大家继续跟我一起学习智能合约系列。

9.函数modifire的强大功能（上）

在solidity的世界里，为我们提供了一种类似于spring切面的操作。可以在我们函数的任意位置插入一个函数方法，我们称之为函数修改器。

下面就让我们来看看他是怎么写的吧~

pragma solidity ^0.4.16;

contract modifireTest
    
    address public ower;
    
    uint public num = 0;
    
    function modifireTest()
        ower = msg.sender;
    
    
    //定义一个函数修改器 
    modifier onlyOwer
        // 不符合条件时 则抛出异常
        require(msg.sender == ower);
        //修饰函数时，函数被插入到'_;'位置
        _;
    
    
    function changeIt(uint _num) onlyOwer
        
        num = _num;
        
    
    

从上面函数我们可以看出，当我们的账户等于我们的部署者时，我们会将_num赋值给num，让我们来执行看看吧

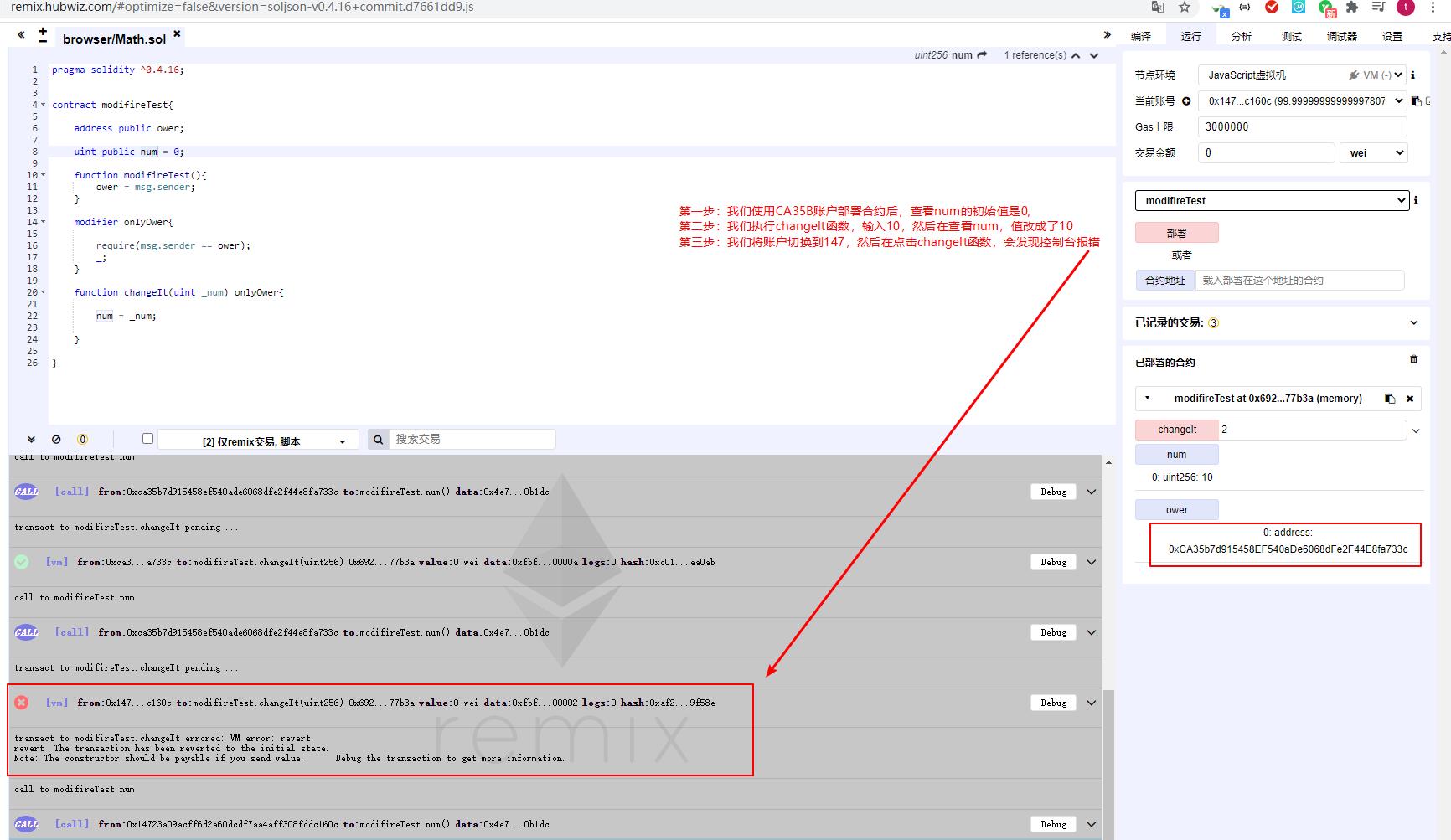
此上的操作符合我们的预期。我们都知道spring利用他的切面特性可以做日志功能等，solidiy的这个函数修改器也是可以增强我们函数的功能，或者是可以做到一些逻辑复用。

10.函数modifire的强大功能（中）

在之前学mapping数据类型的时候，我们举过一个例子，来给我们分配钱包，但是我们怎么验证我们已经给某人分配过钱包了呢？结合我们上小节学的内容，聪明的你是不是已经有方案了呢?

pragma solidity ^0.4.16;

contract mappingTest
  // 映射 一个钱包地址对应一个个人身份id 
  mapping(address => uint) idMapping;
  // 映射 一个个人身份id地址对应一个个人姓名
  mapping(uint => string) nameMapping;
  
  
  uint id = 1;
  // 给某某人提供以太钱包 
  function offerWallet(string name) 
  
      //验证是否还没有给某人分配过钱包
      require(idMapping[msg.sender] == 0);
      
      
      address account = msg.sender;
      // 先给某某人分配一个身份id，然后将钱包绑定到某某人的身份id上
      idMapping[account] = id;
      // 然后在将个人id与个人姓名进行映射绑定
      nameMapping[id] = name;
      
      id++;
     
  
  // 根据地质获取身份id
  function getIdByAddress(address account) view returns(uint)
      
      return idMapping[account];
  
  // 根据id获取个人姓名
  function getNameById(uint id) view returns(string)
      
      return nameMapping[id];
  
   

当然，上述所加的require语句已经满足了我们的要求，但是可不可以写的更好一点呢？

modifier control()
	require(idMapping[msg.sender] == 0);
	_;

我可以可以自定义函数修改器，对函数进行修改。这样，在很多函数都需要做这个校验的时候，我们只需要给那个函数加上control这个修复器作为修饰符即可。

11.函数modifire的强大功能（下）

像我们都应该玩过《是兄弟就来砍我》《山海经》，这类招摇撞骗的游戏吧，不，不是玩过，是看到过。我们不说这个游戏是怎么和那些个明星相互gj来搜刮民脂民膏的。就来想想一个场景。我们经不住诱惑，进到游戏里面后，他告诉我们升级到50级可以领取88元红包，升级到200级，可以体现。假设让你用合约写一个小程序，你会怎么写呢？

pragma solidity ^0.4.16;


contract modifireTest3
    
    
    uint level = 200;
    
    uint money = 0;
    
    uint cash;
    
    modifier modifyLevel(uint _inputLevel)
        
        require(level >= _inputLevel);
        _;
    
    
    function addMoney() modifyLevel(50)
        
        // require(level >= 50);
        
        money = 88;
        
    
    
    
    function recoverCash() modifyLevel(200)
        // require(level >= 200);
        
        money = 0;
        cash = 88;
    
    
    function getMoneyAndCash() view returns(uint,uint)
        return (money,cash);
    
    

如果按照我们常规的写法，我们肯定是在给角色增加现金这个方法中写一个等级判断，给在提现这个方法中也写一个等级判断。的确也是能实现，但是相对来说就啰嗦了不是。作为有经验的开发人员，我们要善于精简提炼我们的代码。这不，solidity的开发人员，已经考虑到我们的“懒惰心理”啦。通过这种方式，是不是发现，人生苦短，我也可以用solidity的modifier了呢？

12.多重modifire的执行顺序

我们在第一次介绍modifier的时候，就说他很像我们spring中的AOP，符合面向切面的思想。

下面我们看的这段代码，大家看看是不是更像呢？

pragma solidity ^0.4.16;

contract modifireTest4
    
    uint public a = 0;
    
    modifier mod1
        
        a = 1;
        
        _;
        
        a = 2;
    
    
    function test() mod1
        
        a = 100;
    
    
    

如果说执行了 test方法后，猜猜a的结果是多少呢？猜对了，答案是2。相当于我们的_（下划线）替代了test函数。那么假如，我们有多个modifier方法呢？来看看他是怎么执行的吧！

pragma solidity ^0.4.16;


contract modifireTest4
    
    uint public a = 0;
    
    modifier mod1
        
        a = 1;
        
        _;
        
        a = 2;
    
    
    modifier mod2
        
        a = 1;
        
        _;
        
        a = 2;
    
    
    function test() mod1 mod2
        
        a = 100;
    
    
    

这个程序大家伙在来猜一下答案呢？我猜大家都猜不对，因为我也猜错了。不卖关子了，我们直接看执行结果吧。

没有猜到吧，答案竟然还是2,这个果然二。那他的执行顺序到底是怎么样子的呢？下面容我给大家说明：

1. a =1
2. mod1执行，进入mod2,a=3
3. mod2替换方法，a=100
4. a=4
5. a=2

我们可以理解为上述的过程，是一个套娃的过程，最终结果还是要看我们的1号种子选手。

所以如是説:modifier多了不可怕,我只認排在首位的老大.

面向区块链编程，构建可信社会。