MIT 18.06 线性代数总结(Part II)
Posted Xurtle
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了MIT 18.06 线性代数总结(Part II)相关的知识,希望对你有一定的参考价值。
引言
终于到了课程的后半部分,它的主题是关于 determinants 和 eigenvalues 的。
Properties of Determinants
教授在整个 lecture 18 中介绍了 Determinants 的10个属性。The determinant is a number associated with any square matrix; we’ll write it as det A or |A|. 文章 summary 中已经把这10个属性整理地很清楚了,没有什么好补充的了。
Determinant Formulas and Cofactors
通过上个小节中介绍的属性 3(b),可以推导出求 2×2 矩阵的行列式的公式,如下图所示。从这个推导过程中可以看出,我们先拆分第一行,得到2个矩阵,然后再把得到的这个2个矩阵分别拆分得到4个矩阵。
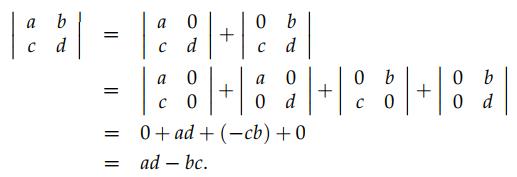
从这个模式中,不难得到3×3矩阵的行列式的公式:我们先拆分第一行,会得到3个矩阵,然后再分别拆分这3个矩阵的第2行,就会得到9个矩阵,然后再分别拆分这9个矩阵的第3行,会得到27个矩阵。幸运的是,这27个矩阵中会得到很多的0,就像2×2 矩阵那样,问题是哪些矩阵会是0呢?从那个2×2 矩阵就可以看出来,同一列上存在超过1个非0元素的矩阵就会为0。因此,这个3×3的矩阵的非0项有 3!=6 个,因此对于 n×n 的矩阵来说,就有 n! 个非0项。这是因为,第1行有n种选择,由于它占了一列,第2行就只有 n-1 种选择了,以此类推,你动手试试马上就明白了。
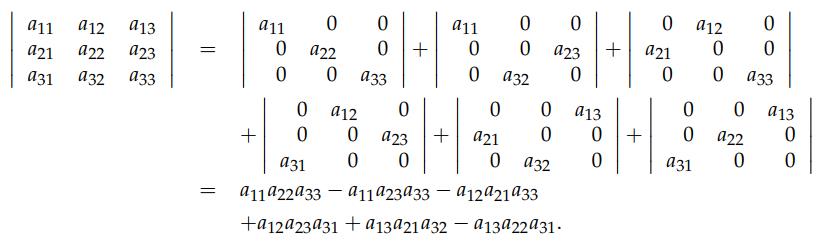
Cofactor formula 实际上就是重写我们上面得到的 determinant Formulas,下图中是沿着 row 1 的 cofactor,你也沿着其它的 rows 计算,哪个 rows 更容易得到矩阵的 determinant 就用哪个。在下图可以看到,第1行的每个元素乘以括号中的 cofactors,不难发现,each cofactor is (plus or minus) the determinant of a 2×2 matrix. 那么如何决定是正的还是负的 determinant 呢?用 (−1)i+j ,比如下图中的例子, a11 的 cofactor 就是正的 determinant,由于i=1,j=1; 而对于 a12 的 cofactor 就是负的 determinant,由于i=1,j=2,你可以做一下 Exercises on determinant formulas and cofactors 中的练习题来巩固一下公式。

在这个 lecture 中,教授用上面得到的公式计算了一下 Tridiagonal matrix 的行列式,we get a sequence which repeats every six terms. 计算过程也很简单,请参考:Tridiagonal matrix
无论是 Determinant Formulas and Cofactors 都是用来求一个矩阵的 determinant 的,对于一个矩阵来说,哪个简单就用哪个方法求解。
Cramer’s Rule, Inverse Matrix and Volume
在前面的小节中,我给出了一个求矩阵的逆的算法,即通过对 [A|I]→[I|A−1] 消元转换的过程。至此,我们可以通过先前学过的知识来得出一个 formula for A−1 ,下面公式中的 CT 是 cofactors
A−1=1detACT
要想证明上述公式的正确性,只需要证明 (detA)I=ACT ,如下图所示,矩阵的第1行 × CT 的第1列实际上就是求矩阵 A 的行列式的 Cofactors 公式,即 detA , 矩阵的第2行 × CT 的第2列也是求矩阵 A 的行列式的 Cofactors 公式,以此类推, ACT 得到的矩阵对角线上应该全部是 det A,接下来如何证明其它的元素都是0呢?其实也很简单,如果你让矩阵的第1行 × CT 的第2列实际上就是矩阵V的行列式,这里矩阵 V 就是把原来矩阵A的第2行用A的第1行取替掉,这就导致了 V 的第1行和第2行相等,因此V是一个 singular 的矩阵,所以 det V=0. 同样的道理,你让矩阵的第1行 × CT 的第3列实际上也是一个矩阵的行列式,这次只不过是把原来矩阵A的第3行用A的第1行取替掉,以此类推。这会导致对角线以外的元素都是0,因此公式可证。
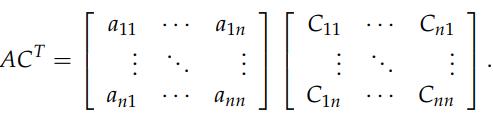
如果你已经理解了 cofactors,Cramer’s Rule 也很好理解,实际的计算中它并没有多大作用,它只不过给了另一种角度去看待公式。计算 inverses 还是用消元来的更有效,这里就不多说它了。
最后是行列式与体积之间的关系:|det A|=volume of box, box 的边是矩阵 A 的列向量。在前面,我已经总结了关于行列式的10个属性,后7个属性是前面3个属性衍生出来的,因此想证明它们的关系,我们只需要证明 volume of box 也满足前面3个属性,证明很简单,不多说了,看一下 lecture 20 马上就能明白了。给出三角形3个顶点的坐标,下图是用行列式计算其面积的公式,在某些情况下,用行列式计算面积要比直接算更为简单,这个公式也更容易记住。同时建议参考一下我总结的多变量微积分的小节:
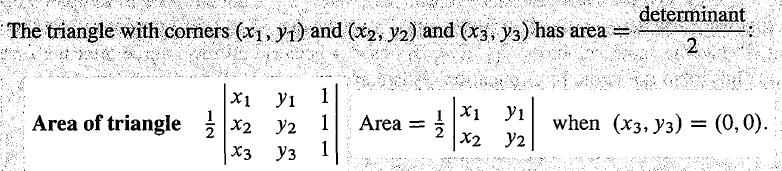
Eigenvalues and Eigenvectors
从几何的角度看 eigenvectors:当矩阵 A 作用于向量 x 时,输出的结果平行 x. 写成代数的形式就是: Ax=λx ,这里的 x 是矩阵 A 的特征向量; λ 是矩阵 A 的特征值。从这个公式不难看出,所有的向量都是 identity matrix 的特征向量,所有的特征值 = 1。注意:特征向量应该是 non-zero 向量。由于等式中有2个未知量(x 和 λ ),我们需要点技巧来解等式。
首先,把等式变换成: Ax−λx=(A−λI)x=0 ,现在很明显,我们要求的特征向量 x 就是 A−λI 的 nullspace,因此要想 nullspace 有 non-zero 的解, A−λI 必须是 singular. 即, det(A−λI)=0 , 求出 λ 以后,接着就可以求出特征向量 x 了。
接下来谈谈矩阵的对角化。If A has n linearly independent eigenvectors, we can put those vectors in the columns of a (square, invertible) matrix S. 如下图所示,我们可以得到: AS=SΛ ,因此 A=SΛS−1
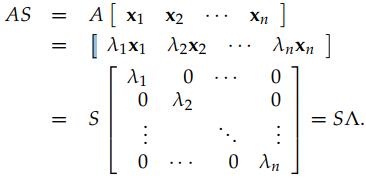
接下来谈谈矩阵 A 的指数。一种角度是:如果 Ax=λx , 那么 A2x=λAx=λ2x . 另一种角度是: A2=SΛS−1SΛS−1=SΛ2S−1 . 因此可得结论: A 的 k 次幂,它的特征向量保持不变,而特征值也变成了 k 次幂。我们还可以得到另一个结论:就是当 |λ|<1,k→∞ 时, Ak→0
从上面的推导过程可以看到,上面得到的所有结论依赖一个条件:A 要有 n 个 independent eigenvectors,否则结论都不成立。如果矩阵 A 的所有 eigenvalues 都不相同,那么它就保证有 n 个 independent eigenvectors. 幸运的是,大多数的矩阵都会有不同的 eigenvalues.
注意:从 Ax=λx 可以看出,有一个特征向量可以得到一个特征值,即一个特征向量对应一个特征值; 但是,多个特征向量有可能对应相同的特征值(比如单位矩阵或者 Finding Eigenvectors with repeated Eigenvalues 中的例子),反过来说是不成立的(多个特征值对应同一个特征向量)。