都2021年了，不会还有人连深度学习还不了解吧-- 优化算法篇

Posted 2022-12-07 奋斗の博客

导读

最近在整理5000粉的粉丝福利，希望大家继续多多支持！你们的支持是我保持更新高质量文章的动力！今天讲述CNN的灵魂所在–优化算法，可以说没有这些优化算法，CNN是无法工作的，巧妇难为无米之炊，如果说数据是CNN的米，那么优化算法可以说是CNN的厨具了。如果你想入坑深度学习，那么请看下去吧！绝对干货满满！

目前深度学习系列已经更新了7篇文章，分别是激活函数篇、卷积篇、损失函数篇、下采样篇、Padding篇、评估指标篇，另有1篇保姆级入门教程，1篇总结性文章CNN中十大令人拍案叫绝的操作，想要入门深度学习的同学不容错过！

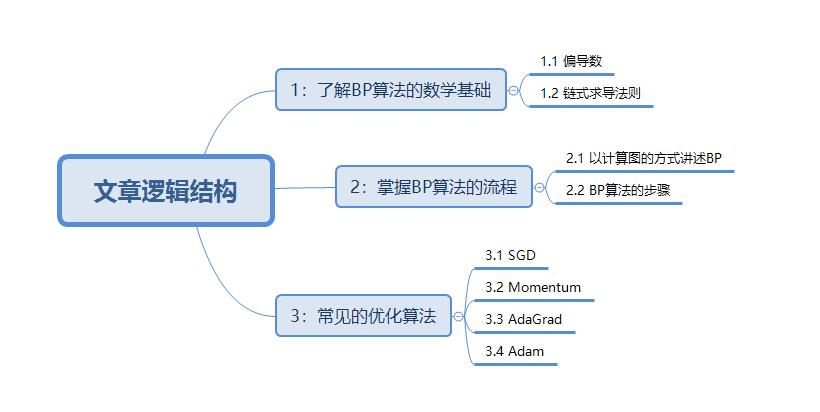
开始讲解之前，希望大家先了解该篇文章的逻辑结构，这对于更深入的阅读文章非常有好处。

一、数学基础

众所周知，入门深度学习需要一定的数学基础，需要掌握的数学知识并不多，想要入坑的小萌新不必担心，这些知识也是高等数学这门课上必学的知识点，在这里简单介绍一下！

1.1 偏导数

在一元函数中，导数就是函数的变化率。在二元函数中，由于自变量多了一个，情况自然要比一元函数复杂的多。

在 xOy 平面内，当动点由 P(x0,y0) 沿不同方向变化时，函数 f(x,y) 的变化快慢一般说来是不同的，因此就需要研究 f(x,y) 在 (x0,y0) 点处沿不同方向的变化率。在这里我们只研究x轴方向和沿y轴方向的变化率，也就是我们大学期间学习过的偏导数。

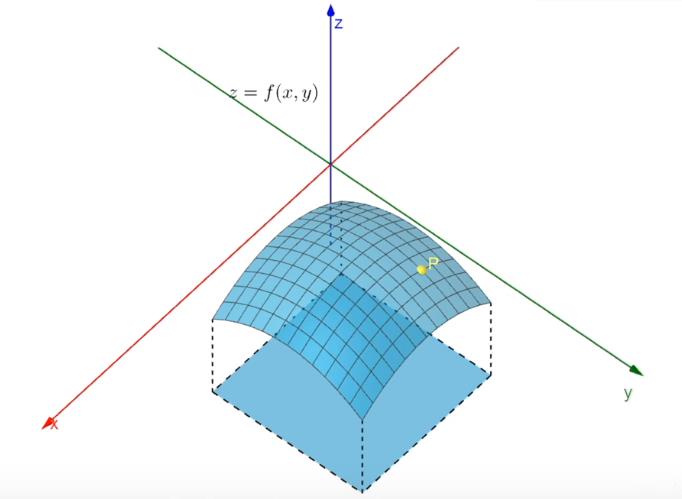
看上图如何来找出沿x轴方向的偏导数和沿y轴方向的偏导数呢？

• x轴方向的偏导数：要求沿x轴方向的偏导数，那一定得先找到沿x轴方向的这条曲线了（联想导数的定义）。
  

• y轴方向的偏导数：要求沿y轴方向的偏导数，那很自然的想到先找到沿y轴方向的这条曲线了（联想导数的定义）。
  

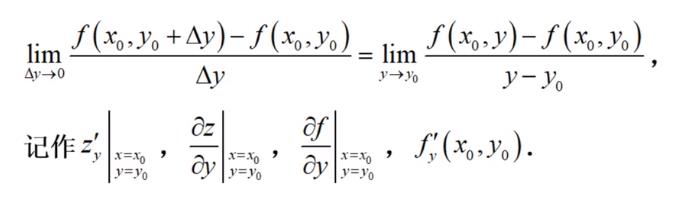
1.2 链式求导法则

链式求导法则的定义如下：如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。
其实非常容易理解，就是引入了一个第三变量，这个变量可以互相抵消，并没有影响最终的结果。

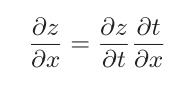
第三变量抵消之后：

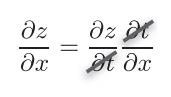
这样做的目的：有时候我们很难求出两个量（假设是L和x）之间的梯度关系，但是我们很容易求出L和t以及t和x之间的关系，这样我们就可以通过链式求导法则求出L和x之间的梯度关系了。

二、BP算法

2.1 加法节点的反向传播

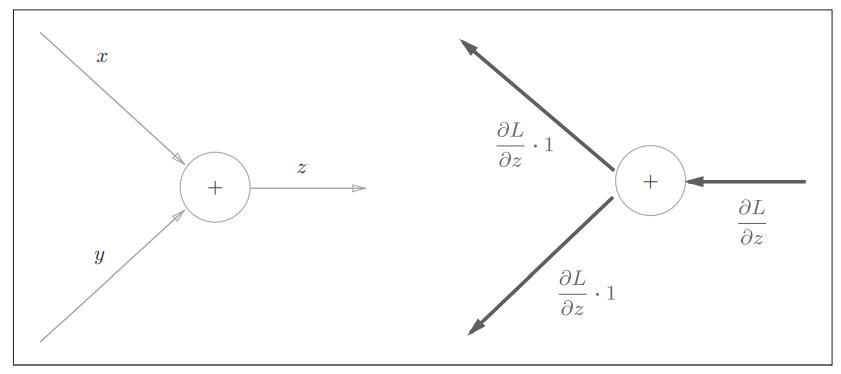
从图中可以看出，加法节点的方向传播仅仅是将前一个神经元的值原封不动的输出到下一个神经元。

2.2 乘法节点的反向传播

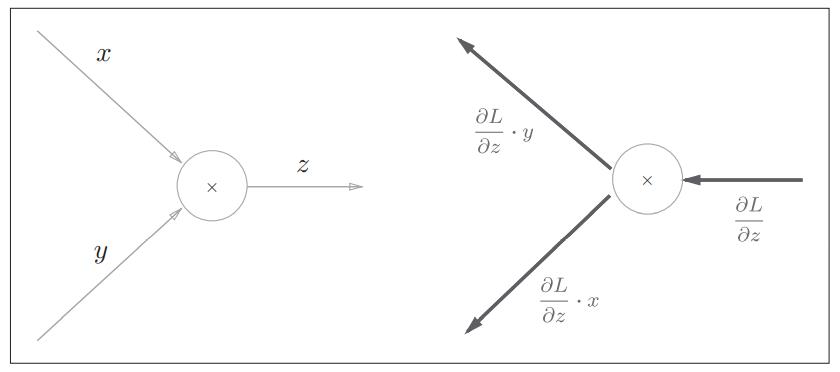
我们考虑z=xy。偏导数用可以用下式表示：

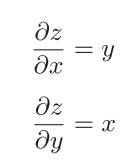
乘法的反向传播会将上一个神经元的值乘以正向传播时的输入信号的“翻转值”后传递给下游。翻转值表示一种翻转关系，如上图所示，正向传播时信号是x的话，反向传播时则是y；正向传播时信号是y的话，反向传播时则是x。

分别理解加法和乘法的反向传播之后，我们剋通过下面这个案例来巩固一下。

2.3 计算图方式理解BP算法

我们在正式讲述BP算法之前，先来看一下案例，这个案例掌握了，BP算法就迎刃而解了。首先，我们需要计算每个节点的反向传播的值。

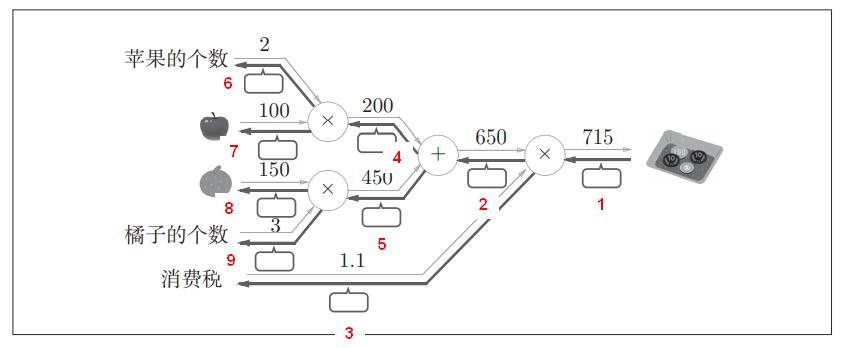
前向传播过程在这里省略了，按照流程一步一步走就行了！在这里详细介绍反向传播的计算过程。
反向传播详细计算过程：

标号	计算过程
1	715 / 715 = 1
2	1 * 1.1 = 1.1
3	1 * 650 = 650
4	1.1（+法节点原封不动的传回去）
5	1.1（+法节点原封不动的传回去）
6	1.1 * 100 = 110
7	1.1 * 2 = 2.2
8	1.1 * 3 = 3.3
9	1.1 * 150 = 165

计算完成后，得到下图。

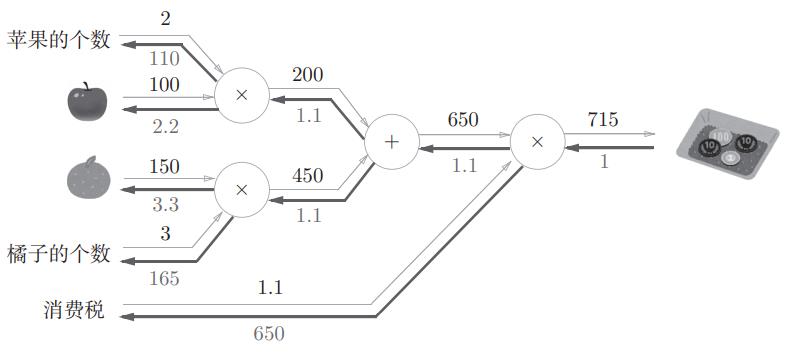
相信通过这个案例，大家已经对反向传播算法有所了解了，趁热打铁，我们直接看一下BP反向传播算法的流程。

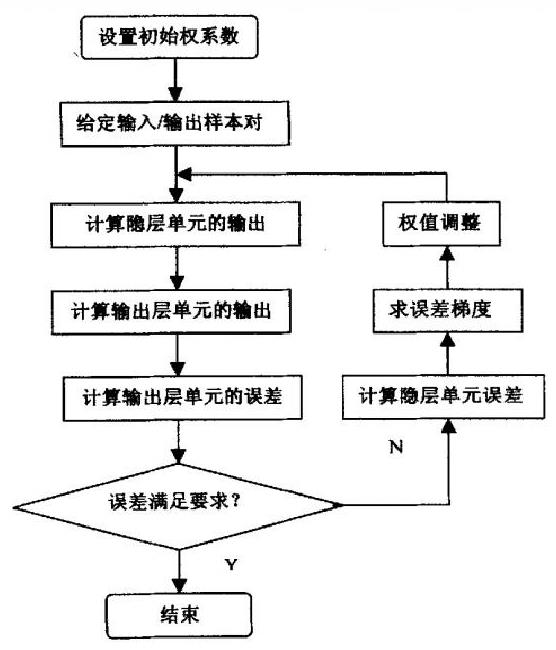
2.2 BP算法的流程

在这里只简单介绍一下BP算法的大致步骤，具体计算过程网络上已经有很多文章，有些写的还不错，这里就不详细描述了！大家自行到网络上查阅！

三、常见的优化算法

神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题，解决这个问题的过程称为最优化。然而这个探索的过程是非常困难的，因为神经网络模型的参数空间是非常复杂的，是不可估计的。

为此，科学家以梯度为线索，使用参数的梯度，沿着梯度的方向更新参数，并重复这个步骤多次，从而逐渐靠近最优解，以上的这个过程被称为随机梯度下降法，也就是大家所熟知的SGD。

对于SGD的描述，有一段话描述的非常到位，引用自《深度学习入门：基于Python的理论与实现》，这本书也是我一直在推荐的：

有一个性情古怪的探险家。他在广袤的干旱地带旅行，坚持寻找幽深的山谷。他的目标是要到达最深的谷底（他称之为“至深之地”）。这也是他旅行的目的。并且，他给自己制定了两个严格的“规定”：一个是不看地图；另一个是把眼睛蒙上。因此，他并不知道最深的谷底在这个广袤的大地的何处，而且什么也看不见。在这么严苛的条件下，这位探险家如何前往“至深之地”呢？他要如何迈步，才能迅速找到“至深之地”呢？
寻找最优参数时，我们所处的状况和这位探险家一样，是一个漆黑的世界。我们必须在没有地图、不能睁眼的情况下，在广袤、复杂的地形中寻找“至深之地”。大家可以想象这是一个多么难的问题。在这么困难的状况下，地面的坡度显得尤为重要。探险家虽然看不到周围的情况，但是能够知道当前所在位置的坡度（通过脚底感受地面的倾斜状况）。于是，朝着当前所在位置的坡度最大的方向前进，就是SGD的策略。勇敢的探险家心里可能想着只要重复这一策略，总有一天可以到达“至深之地”。

优化算法主要有以下的几种，当然现在有越来越多的研究者在研究效果更好的优化算法，但基本上都是对SGD算法的改进及再改进，因此，掌握好SGD及其它常用的优化算法，是

3.1 随机梯度下降法（SGD）

SGD可以简单概括为：

W指的是权重参数，把损失函数关于权重参数W的梯度记为：

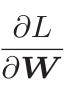
η表示学习率，是一个常数，实际上会取0.01或0.001这些事先决定好的值，当然具体的取值并没有一个统一的规定，一个网络结构有一个网络结构的取法。这个需要通过后期阅读大量的论文汲取经验。

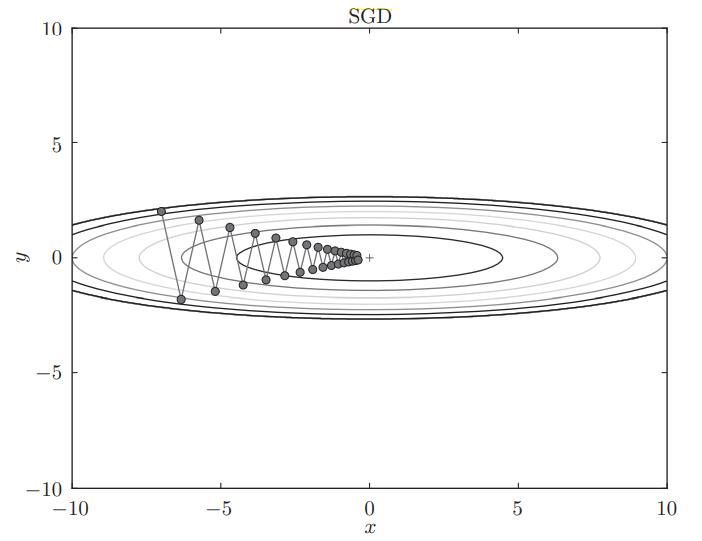
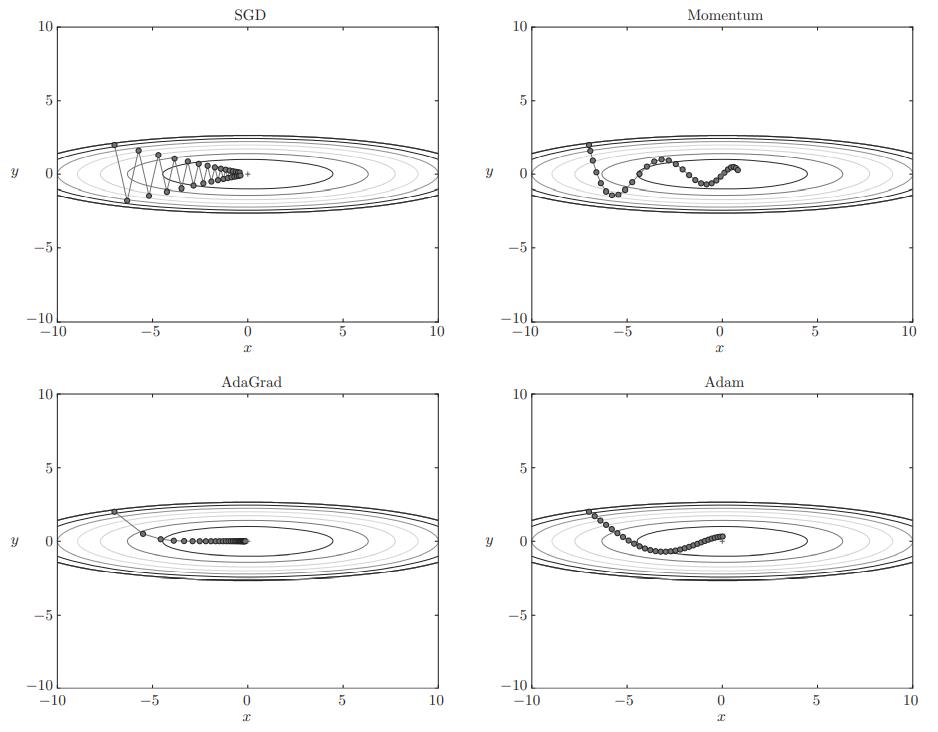
由上图看出，SGD优化策略呈”之“字形移动，无疑这是一种非常低效的路径。造成这种现象的根本原因在于梯度的方向并没有指向最小值的方向。

3.2 Momentum

Momentum是“动量”的意思，用数学式表示Momentum方法如下所示：

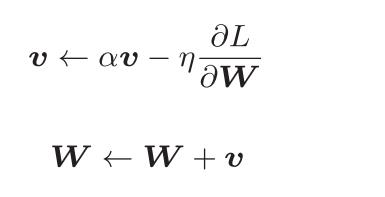
W表示要更新的权重参数，η表示学习率（也被称为步长），这里新出现了一个变量v，对应物理上的速度。表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加这一物理法则。αv这一项表示在物体不受任何力时，该项承担使物体逐渐减速的任务（α设定为0.9之类的值），对应物理上的地面摩擦或空气阻力。

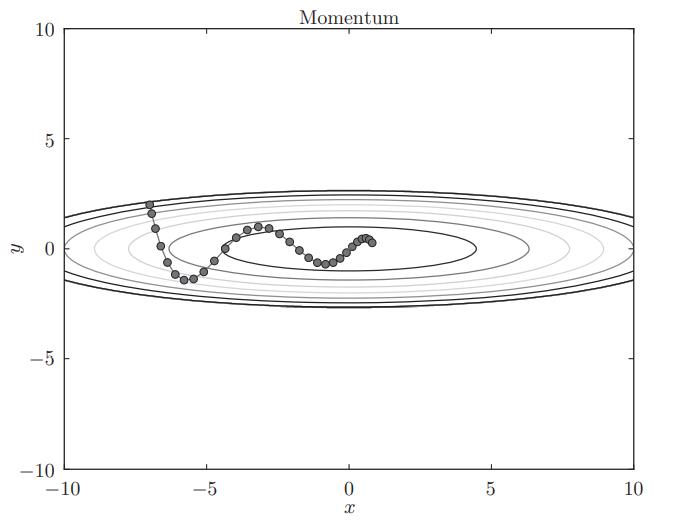
和SGD相比，我们发现“之”字形的“程度”减轻了。这是因为虽然x轴方向上受到的力非常小，但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽然y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它们会互相抵消，所以y轴方向上的速度不稳定。因此，和SGD时的情形相比，可以更快地朝x轴方向靠近，减弱“之”字形的变动程度。

3.3 AdaGrad

在深度学习领域中，学习率（也称为步长）是一个非常非常重要的超参数，学习率过大，在解空间内不能找到一个全局的最优解，导致学习发散而不能正确进行训练；学习率过小，则会导致学习耗费大量的时间，这都是不可取的。鉴于这个问题，研究者发现了一种调学习率的有效技巧，这种技巧被称为学习率衰减。

这里新出现了变量h，它保存了以前的所有梯度值的平方和，然后，在更新参数时，通过乘以 1/根号下h，就可以调整学习的尺度。这意味着，参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。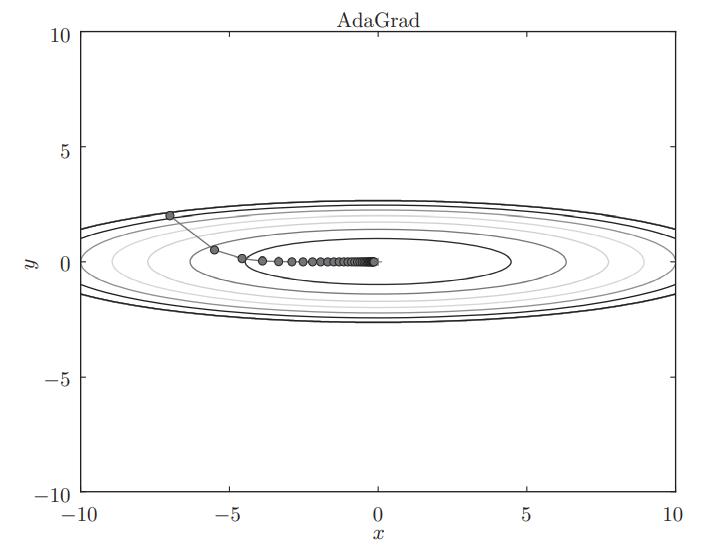

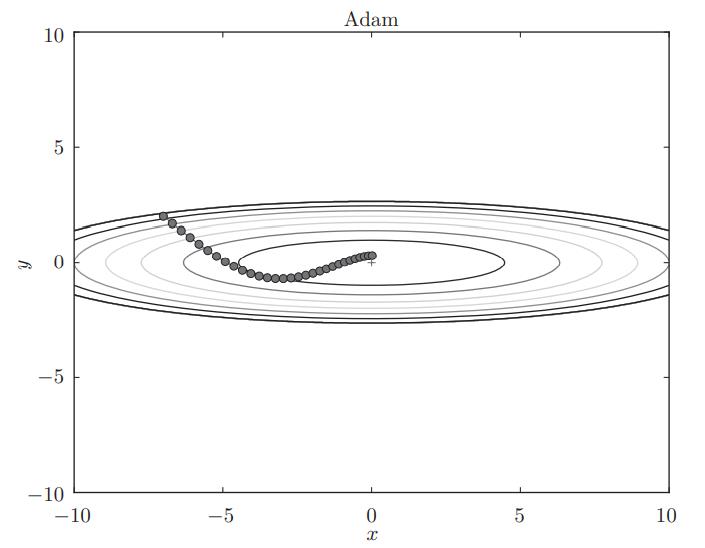
3.4 Adam

Adam是综合了Momentum的特点和AdaGrad的特点，是这两种方法融合之后的一种优化策略。该方法理论有些复杂，单纯靠一篇文章的一小节内容不可能完全讲清楚，因此，强烈推荐大家去看原论文。论文链接：https://arxiv.org/abs/1412.6980v8

Adam会设置 3个超参数。一个是学习率，另外两个是一次momentum系数β1和二次momentum系数β2。根据论文，标准的设定值是β1为 0.9，β2 为 0.999。设置了这些值后，大多数情况下都能顺利运行。

总结

优化算法有很多，但是基本上都是在SGD的基础上修改的，明白了SGD的优化策略后，其它的优化策略也可以很容易的理解，而且现在的深度学习框架例如PyTorch已经集成了各种优化策略，不需要我们自己实现。
根据使用的方法不同，参数更新的路径也不同。只看图的话，AdaGrad似乎是最好的，不过也要注意，结果会根据要解决的问题而变。并且，很显然，超参数（学习率等）的设定值不同，结果也会发生变化。

文章持续更新，可以关注微信公众号【医学图像人工智能实战营】获取最新动态，一个专注于医学图像处理领域前沿科技的公众号。坚持以实践为主，手把手带你做项目，打比赛，写论文。凡原创文章皆提供理论讲解，实验代码，实验数据。更有上百部深度学习入门资料免费等你来拿，只有实践才能成长的更快，关注我们，一起学习进步~

计划

深度学习保姆级入门教程 – 论文+代码+常用工具
1个字，绝! – CNN中十大令人拍案叫绝的操作
都2021年了，不会还有人连深度学习还不了解吧？（一）-- 激活函数篇
都2021年了，不会还有人连深度学习还不了解吧？（二）-- 卷积篇
都2021年了，不会还有人连深度学习还不了解吧？（三）-- 损失函数篇
都2021年了，不会还有人连深度学习还不了解吧？（四）-- 上采样篇
都2021年了，不会还有人连深度学习还不了解吧？（五）-- 下采样篇
都2021年了，不会还有人连深度学习还不了解吧？（六）-- Padding篇
都2021年了，不会还有人连深度学习还不了解吧？（七）-- 评估指标篇
都2021年了，不会还有人连深度学习还不了解吧？（八）-- 优化算法篇
都2021年了，不会还有人连深度学习还不了解吧？（九）-- 注意力机制篇
都2021年了，不会还有人连深度学习还不了解吧？（十）-- 数据归一化篇

觉得写的不错的话，欢迎点赞+评论+收藏，欢迎关注我的微信公众号，这对我帮助真的很大很大很大！