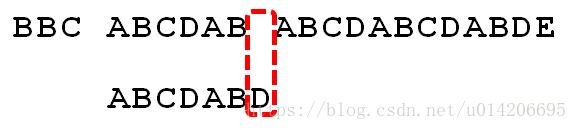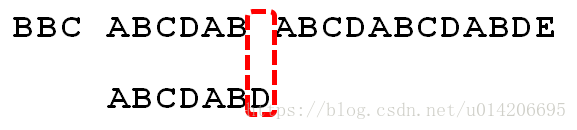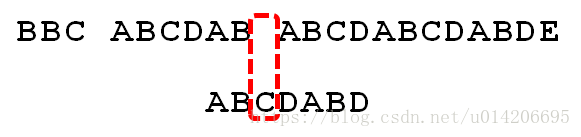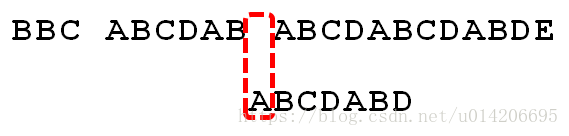数据结构-串的模式匹配

Posted 2023-04-22

参考技术A 串的模式匹配就是子串定位操作。给定两个串s="s0 s1 ... s(n-1)"和t="t0 t1 ... t(m-1)"（其中n和m分别是串s和t的长度），在主串s中寻找子串t的过程称为模式匹配，t称为模式。如果在s中找到等于t的子串，则称匹配成功，返回t在s中的首次出现的下标位置；否则匹配失败，返回-1。

本文介绍三个串模式匹配算法，分别是简单回溯算法（Brute-Force，BF算法）、KMP算法、KMP算法的改进。

从主串s的第0个字符开始，与模式串t的第0个字符开始逐字符比较，不相同时回溯到模式串t的第0个和主串s的第1个字符，重新开始比较。以此类推，直到t的所有字符完成匹配，则匹配成功，否则匹配失败。

BF算法速度慢的原因是存在大量不必要的回溯，即在某一趟与t的匹配过程失败后，需要返回s串开始字符的下一字符重新开始比较，这对于某些模式串t来说是不必要的。例如，若s=12123123132，t=12313，在t与12 12312 3132中加粗子序列进行比较时，在 2 处发生失配，BF算法接下来将t与121 23123 132、1212 31231 32、12123 12313 2比较。由于t中的231、312与其开始的123并不相同，显然t与121 23123 132、1212 31231 32的比较是不必要的。

KMP算法就是利用模式串中与模式串开头部分子串的重复性来减少重复回溯，实现新一轮比较的直接跳转。 具体来说，KMP算法利用一个数组记录模式串中每一个字符前面有几个字符与模式串从头重复，在与s串比较失配时，直接跳转到重复子串的下一个字符继续比较，而不用跳转至模式串t的第0个字符。

算法步骤： ①计算跳转数组next。②利用KMP算法进行模式匹配。

next数组通过递推计算，即如果当前字符 t[j] 的前一个字符 t[j-1] 与其 next[j-1] 指向的字符 t[next[j-1]] 相同，意味着 t[j] 前的 next[j-1]+1 个字符与从 t[0] 到 t[next[j-1]] 的子串相同，因此 next[j]=next[j-1]+1 ；如果不相同，则递推至 t[next[j-1]] 的next值指向的字符，与 t[j-1] 比较，直到确认 t[j] 前与 t 串从头重复的字符数，或者无重复字符标记为 0 。

注意此处的函数返回参数类型为int*，用于 返回一位数组 ，且返回的这个一位数组必须在函数中用static定义。

KMP算法进行模式匹配时，只需在回溯时将 j 指针赋值为 next[j] 。需要注意的是，若 next[j] 为 -1 ，则意味着 t[j] 前面没有与 t 从头重复的字符，且 t[j] 与 s[i] 失配，则 i 和 j 均加 1 。

考虑更特殊的模式串，还能进一步减少不必要的回溯次数。例如，s=111211112，t=11112，按照上述next的计算方式，next=-1,0,1,2,3。当 i=3, j=3 时失配，此时 s[i]=2, t[j]=1 ，由于 next[j]=2 ，于是 j 跳转为 2 ，t=11 1 12与s=111 2 11112比较。由于 t[next[j]]=t[j] 也为 1 ，必然与 s[i]=2 不相同，显然这次回溯也不必要。

总结来说， 当失配的字符与待跳转的字符相同时，跳转一步并无意义，可再跳一步 ，即将当前字符置为跳转后字符的next值。

串的模式匹配算法之kmp

---

title: 串的模式匹配算法之kmp

tags: 数据结构与算法之美

author: 辰砂

---

1.引言

首先我们需要了解串的模式算法目的：确定主串中所含子串第一次出现的位置（定位）；常见的算法种类： BF算法（又称古典的、经典的、朴素的、穷举的），KMP算法（特点：速度快）。网上有很多帖子，博客写的都特别好，这篇文章也是对自己的一个总结。

2.BF算法

BF算法设计思想：

---

将主串的第pos个字符和模式的第一个字符比较
若相等，继续逐个比较后续字符；
若不等，从主串的下一字符起，重新与模式的第一个字符比较。
直到主串的一个连续子串字符序列与模式相等 。
返回值为S中与T匹配的子序列第一个字符的序号，即匹配成功。
否则，匹配失败，返回值 0

---

1.举例：

假设现在我们面临这样一个问题：有一个文本串S，和一个模式串P，现在要查找P在S中的位置，怎么查找呢？

 

如果用暴力匹配的思路，并假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置，则有：

如果当前字符匹配成功（即S[i] == P[j]），则i++，j++，继续匹配下一个字符；

如果失配（即S[i]! = P[j]），令i = i - (j - 1) （表示主串的位置回到当前的下一个位置），j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。

1. public static int bfMatch(char[] s, char[] p) {
   int sLen = s.length;
   int pLen = p.length;
   int i = 0;
   int j = 0;
   while (i < sLen && j < pLen) {
   if (s[i] == p[j]) {
   //①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++
   i++;
   j++;
   } else {
   //②如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0
   // i - (j - 1) 表示主串的位置回到当前的下一个位置。
   i = i - j + 1;
   j = 0;
   }
   }
   //匹配成功，返回模式串p在文本串s中的位置，否则返回-1
   if (j == pLen) {
   return i - j;
   } else {
   return -1;
   }
   }
   public static void main(String[] args) {
   String s = "BBC ABCDAB ABCDABCDABDE";
   String p = "ABCDABD";
   System.out.println(bfMatch(s.toCharArray(),p.toCharArray()));
   }

    

2.时间复杂度说明：

若n为主串长度，m为子串长度，最坏情况是 主串前面n-m个位置都部分匹配到子串的最后一位，即这n-m位各比较了m次 最后m位也各比较了1次

总次数为：(n-m)m+m＝(n-m+1)m 若m<<n，则算法复杂度o(n*m)< p="">

网上有个很好的例子，故引用：

举个例子，如果给定文本串S“BBC ABCDAB ABCDABCDABDE”，和模式串P“ABCDABD”，现在要拿模式串P去跟文本串S匹配，整个过程如下所示：

1.S[0]为B，P[0]为A，不匹配，执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[1]跟P[0]匹配，相当于模式串要往右移动一位（i=1，j=0）

2.S[1]跟P[0]还是不匹配，继续执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，S[2]跟P[0]匹配（i=2，j=0），从而模式串不断的向右移动一位（不断的执行“令i = i - (j - 1)，j = 0”，i从2变到4，j一直为0）

3.直到S[4]跟P[0]匹配成功（i=4，j=0），此时按照上面的暴力匹配算法的思路，转而执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，可得S[i]为S[5]，P[j]为P[1]，即接下来S[5]跟P[1]匹配（i=5，j=1）

4.S[5]跟P[1]匹配成功，继续执行第①条指令：“如果当前字符匹配成功（即S[i] == P[j]），则i++，j++”，得到S[6]跟P[2]匹配（i=6，j=2），如此进行下去

5.直到S[10]为空格字符，P[6]为字符D（i=10，j=6），因为不匹配，重新执行第②条指令：“如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0”，相当于S[5]跟P[0]匹配（i=5，j=0）

6.至此，我们可以看到，如果按照暴力匹配算法的思路，尽管之前文本串和模式串已经分别匹配到了S[9]、P[5]，但因为S[10]跟P[6]不匹配，所以文本串回溯到S[5]，模式串回溯到P[0]，从而让S[5]跟P[0]匹配。

而S[5]肯定跟P[0]失配。为什么呢？因为在之前第4步匹配中，我们已经得知S[5] = P[1] = B，而P[0] = A，即P[1] != P[0]，故S[5]必定不等于P[0]，所以回溯过去必然会导致失配。那有没有一种算法，让i 不往回退，只需要移动j 即可呢？

3.KMP算法（主串指针不回溯）

算法思想：利用已经部分匹配的结果而加快模式串的滑动速度？且主串S的指针i不必回溯！可提速到O(n+m)！

算法步骤： 下面先直接给出KMP的算法流程：

---

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置

 

如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++，继续匹配下一个字符；

 

如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。

 

换言之，当匹配失败时，模式串向右移动的位数为：失配字符所在位置 - 失配字符对应的next 值（next 数组的求解会在下文的3.3.3节中详细阐述），即移动的实际位数为：j - next[j]，且此值大于等于1。

 

---

很快，你也会意识到next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

此也意味着在某个字符失配时，该字符对应的next 值会告诉你下一步匹配中，模式串应该跳到哪个位置（跳到next [j] 的位置）。如果next [j] 等于0或-1，则跳到模式串的开头字符，若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头，且具体跳过了k 个字符。

public static int kmpMatch(char[] s, char[] p) {
int sLen = s.length;
int pLen = p.length;
int i = 0;
int j = 0;
while (i < sLen && j < pLen) {
if (s[i] == p[j]) {
//①如果当前字符匹配成功（即S[i] == P[j]），则i++，j++
i++;
j++;
} else {
j = next[j];
}
}
//匹配成功，返回模式串p在文本串s中的位置，否则返回-1
if (j == pLen) {
return i - j;
} else {
return -1;
}
}

 

为此,定义next[j]函数，表明当模式中第j个字符与主串中相应字符“失配”时，在模式中需重新和主串中该字符进行比较的字符的位置。

1.如何求next()?

1.寻找前缀后缀最长公共元素长度

比如 字符串 ‘a’ 的前缀就是为空，后缀也是为空，所以前缀后缀的意思，是不包括当前字符串，字符串 ‘ab’ 的前缀是a，后缀是b。

定义： 对于P = p0 p1 ...pj-1 pj，寻找模式串P中长度最大且相等的前缀和后缀。如果存在p0 p1 ...pk-1 pk = pj- k pj-k+1...pj-1 pj，那么在包含pj的模式串中有最大长度为k+1的相同前缀后缀。

比如：

j	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
模式串	a	b	c	a	a	b	c	a	b	c	a	a	a	b	d	a	b
前后缀最长公共元素	0	0	0	1	1	2	3	1	2	3	4	5	6	2	0	1	2

 

 

 

2.求next数组

next 数组考虑的是除当前字符外的最长相同前缀后缀，所以通过第①步骤求得各个前缀后缀的公共元素的最大长度后，只要稍作变形即可：将第①步骤中求得的值整体右移一位，然后初值赋为-1，如下表格所示：

j	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
模式串	a	b	c	a	a	b	c	a	b	c	a	a	a	b	d	a	b
next[j]	0	1	1	1	2	2	3	1	1	2	3	4	5	6	2	1	2

 

 

 

 

 

 

3.如何求next函数值

1. next[1] = 0;表明主串从下一字符si+1起和模式串重新开始匹配。i = i+1; j = 1;

    

2. 设next[j] = k，则next[j+1] = ?

    

   ①若pk=pj，则有“p1…pk-1pk”=“pj-k+1…pj-1pj” ，如果在 j+1发生不匹配，说明next[j+1] = k+1 = next[j]+1。

    

   ②若pk≠pj，可把求next值问题看成是一个模式匹配问 题，整个模式串既是主串，又是子串。

    

   

若pk’=pj，则有“p1…pk’”=“pj-k’+1…pj”， next[j+1]=k’+1=next[k]+1=next[next[j]]+1.

若pk”=pj ，则有“p1…pk””=“pj-k”+1…pj”， next[j+1]=k”+1=next[k’]+1=next[next[k]]+1. next[j+1]=1.

 

 

4.总结

核心的点在于：以前的bf算法是需要i进行回溯，导致时间复杂度O(m*n) ,现在kmp算法的核心是i不进行回溯，而j这个值不确定，根据串的规律，主串前面匹配成功的串前缀和后缀相等的地方不需要匹配即可。这样的时间复杂度是O(m + n)

引用博客例子：

1.最开始匹配时

P[0]跟S[0]匹配失败

 

所以执行“如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]”，所以j = -1，故转而执行“如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++”，得到i = 1，j = 0，即P[0]继续跟S[1]匹配。

 

P[0]跟S[1]又失配，j再次等于-1，i、j继续自增，从而P[0]跟S[2]匹配。

 

P[0]跟S[2]失配后，P[0]又跟S[3]匹配。

 

P[0]跟S[3]再失配，直到P[0]跟S[4]匹配成功，开始执行此条指令的后半段：“如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++”。

 

 

2.P[1]跟S[5]匹配成功，P[2]跟S[6]也匹配成功, ...，直到当匹配到P[6]处的字符D时失配（即S[10] != P[6]），由于P[6]处的D对应的next 值为2，所以下一步用P[2]处的字符C继续跟S[10]匹配，相当于向右移动：j - next[j] = 6 - 2 =4 位。

3.向右移动4位后，P[2]处的C再次失配，由于C对应的next值为0，所以下一步用P[0]处的字符继续跟S[10]匹配，相当于向右移动：j - next[j] = 2 - 0 = 2 位。

4.移动两位之后，A 跟空格不匹配，模式串后移1 位。

5.P[6]处的D再次失配，因为P[6]对应的next值为2，故下一步用P[2]继续跟文本串匹配，相当于模式串向右移动 j - next[j] = 6 - 2 = 4 位。

6.匹配成功，过程结束。

匹配过程一模一样。也从侧面佐证了，next 数组确实是只要将各个最大前缀后缀的公共元素的长度值右移一位，且把初值赋为-1 即可。

代码如下：

void get_next(SString T, int &next[])
{
i= 1; next[1] = 0; j = 0;
while( i<T[0]){
if(j==0 || T[i] == T[j]){
++i; ++j;
next[i] = j;
}
else
j = next[j];
}
}

 

kMP算法的时间复杂度

设主串s的长度为n,模式串t长度为m,在KMP算法中求next数组的时间复杂度为O(m),在后面的匹配中因主串s的下标不减即不回溯,比较次数可记为n,所以KMP算法总的时间复杂度为O(n+m)

---

参考原文：https://blog.csdn.net/vjulyv/article/details/7041827?utm_source=copy