机器学习总结四：逻辑回归与反欺诈检测案例

Posted 2022-12-07 想考个研

机器学习算法总结

一、Bagging之决策树、随机森林原理与案例

二、boosting之GBDT、XGBT原理推导与案例

三、SVM原理推导与案例

四、逻辑回归与反欺诈检测案例

五、聚类之K-means

---

四、逻辑回归

1、概述

1. 由线性回归变化而来的，应用于分类问题中的广义回归算法。

2. 组成：

   • 回归函数
     $$z=w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b=\left[\begin{array}{c}{w}_1{w}_2{w}_{n}b\end{array}\right]\ast \left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\\ 1\end{array}\right]=w^{T}X$$

• 激活函数/sigmoid函数

$$g(z)=\frac{1}{1+e^{-z}}$$

$$\begin{array}{lc}\frac{{\delta }^{\prime }g(z)}{\delta z}& =-(1+e^{-z}{)}^{-2}\ast e^{-z}\ast -1=\frac{e^{-z}}{(1+e^{-z}{)}^2}=\frac{1}{1+e^{-z}}\ast \frac{1+e^{-z}-1}{1+e^{-z}}\\ & =sigmoid\ast (1-sigmoid)\end{array}$$

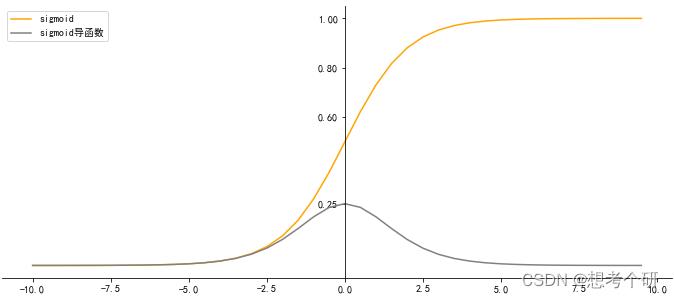
3. 机率/统计学几率：事件发生的概率与该事件不发生的概率的比值

4. 对数几率：分类为1的概率/分类不为1的概率的比值再取对数
   $$ln(\frac{g(z)}{1-g(z)})=ln(\frac{\frac{1}{1+e^{-z}}}{1-\frac{1}{1+e^{-z}}})=ln(e^z)=z$$
   可以看出：逻辑回归中线性回归部分预测结果是在求预测为1的几率(取对数)

2、原理

2.1、损失函数

衡量参数w优劣的评估指标，用来求解最优参数的工具。

注：没有“求解参数”需求的模型没有损失函数，比如决策树、knn、随机森林
$$\begin{gathered} J(w)=-\sum _{i=1}^n[y_{i}lo{g}_{2}g(x_i)+(1-y_i)lo{g}_2(1-g(x_i))] \\ n:样本数量；x_i,y_i：样本特征和真实标签 \end{gathered}$$

2.2、损失函数推导方式1

对 于 二 分 类 为 例 ： 设 p = g ( y i ^ = 1 ∣ x i ,