二叉搜索树的概念 及 功能代码实现

Posted 2022-12-06 小乔不掉发

1、概念：

二叉搜索树 又称 二叉排序树

特点：

• 二叉树 每个节点中保存关键字（key）（关键字需要具备 比较 的能力）
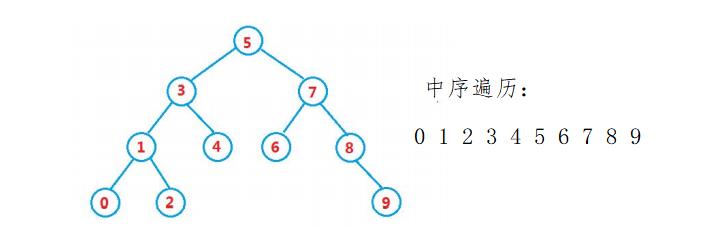
• 每个节点 都是 大于左子树，小于右子树
• 二叉树搜索树中 不会出现 相等的 key
• 中序遍历 一定是 有序的
  
• 时间复杂度：最好和平均：O(log(n)) 最坏：O(n)

通过平衡树，解决搜索树最坏情况：
二叉搜索树的平衡树（AVL树 + 红黑树）

AVL树：

前提是，二叉搜索树，要求 每个结点 的 左右子树高度差 的绝对值 不超过1

AVL 的查找操作等同于普通搜索树的查找
AVL 的插入操作，需要多一步维护操作（借助旋转完成）

特点： 高度不会太夸张，时间复杂度控制在 O(nloog(n))

红黑树：

相对平衡树

性质：

• 1、树的结点标记颜色（红 或 黑）
  
• 2、树的 根 如果存在，一定是 黑色
• 3、树的 ” 叶子结点 “（叶子结点的空结点），看做黑色
• 4、树中 红色结点 的 相邻 不能是红色
  （假如 node 是红色。则 node.parent | node.left | node.right 不能是红色）
• 5、从 根 到 任意叶子，所有路径上，黑色的数量需要保持一致
  

2、二叉搜索树的操作：

（1）查找操作：

    //查找
    public boolean search(Integer key) 
        Node cur = root;
        while (cur != null) 
            int cmp = key.compareTo(cur.key);
            if (cmp == 0) 
                return true;
             else if (cmp < 0) 
                cur = cur.left;
             else 
                cur = cur.right;
            
        
        return false;
    

（2）插入操作：

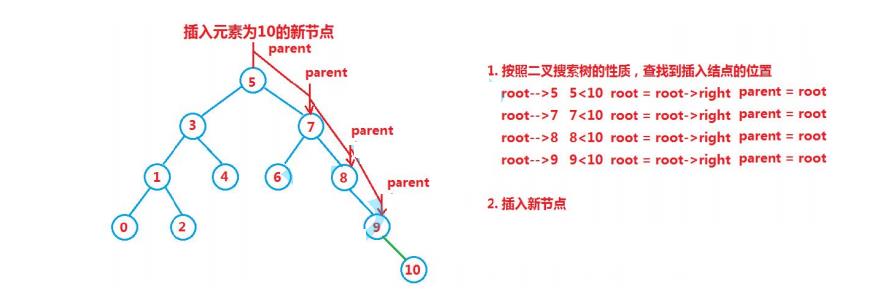
• 1、如果树是空树，即根 == null，直接插入
  
• 2、如果树不是空树，按照查找逻辑确定插入位置，插入新节点
  

    //插入
    public void insert(Integer key)
        //空树
        if (root == null) 
            root = new Node(key);
            return;
        
        //始终保持 parent 是 cur 的双亲节点
        Node parent = null;
        Node cur = root;
        int cmp = 0;
        while (cur != null) 
            cmp = key.compareTo(cur.key);
            if (cmp == 0) 
                //说明二叉树中已经有该节点，直接抛异常
                throw new RuntimeException("BST 中不允许出现两个相同的数");
             else if (cmp < 0) 
                parent = cur;
                cur = cur.left;
             else 
                parent = cur;
                cur = cur.right;
            
        
        //cur 已经到了要插入的位置了
        Node newNode = new Node(key);
        if (cmp < 0) 
            parent.left = newNode;
         else 
            parent.right = newNode;
        
    

（3）删除操作：

待删除结点为 cur, 待删除结点的双亲结点为 parent

• 1、cur.left == null
  （1）cur 是 root，则 root = cur.right
  （2）cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
  （3）cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
• 2、cur.right == null
  （1） cur 是 root，则 root = cur.left
  （2）cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
  （3）cur 不是 root，cur 是 parent.right，则 parent.right = cur.left
• 3、 cur.left != null && cur.right != null
  需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被
  删除节点中，再来处理该结点的删除问题

    //删除
    public boolean remove(Integer key) 
        Node cur = root;//要删除的节点
        Node parent = null;//cur 的双亲节点
        //找到要删除的元素
        while (cur != null) 
            int cmp = key.compareTo(cur.key);
            if (cmp == 0) 
                removeInternal(cur,parent);
                return true;
             else if (cmp < 0) 
                parent = cur;
                cur = cur.left;
             else 
                parent = cur;
                cur = cur.right;
            
        
        //没找到要删除的元素
        return false;
    

    private void removeInternal(Node cur, Node parent) 
        //1、要删除的结点是 叶子结点
        if (cur.left == null && cur.right == null) 
            if (cur == root) 
                root = null;
             else if (cur == parent.left)
                //要删除的结点是其父节点的左孩子
                parent.left = null;
             else 
                //要删除的结点是其父节点的右孩子
                parent.right = null;
            
         else if (cur.left != null && cur.right == null) 
            //2、要删除的结点只有 左孩子
            if (cur == root) 
                root = cur.left;
             else if (cur == parent.left)
                //要删除的结点是其父节点的左孩子,让他自己的左孩子代替他的位置
                parent.left = cur.left;
             else 
                //要删除的结点是其父节点的右孩子,让他自己的左孩子代替他的位置
                parent.right = cur.left;
            
         else if (cur.left == null && cur.right != null) 
            //3、要删除的结点只有 右孩子
            if (cur == root) 
                root = cur.right;
             else if (cur == parent.left)
                //要删除的结点是其父节点的左孩子,让他自己的左孩子代替他的位置
                parent.left = cur.right;
             else 
                //要删除的结点是其父节点的右孩子,让他自己的左孩子代替他的位置
                parent.right = cur.right;
            
         else 
            //4、要删除的结点，左右孩子都有（采用替换法删除）
            //使用 cur 的左子树中的做大值所在的结点，记作 ghost，ghost 的双亲记作 ghostParent
            Node ghost = cur.left;
            Node ghostParent = null;
            //一路向右查找，直到 ghost.right == null
            if (ghost.right != null) 
                ghostParent = ghost;
                ghost = ghost.right;
            
            //（1）替换
            cur.key = ghost.key;
            //（2）删除 ghost 结点（其右孩子一定为空）
            if (cur == ghostParent) 
                ghostParent.left = ghost.left;
             else 
                ghostParent.right = ghost.left;
            
        
    

3、二叉搜索树和 java 类集的关系：

TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set；实际上用的是红黑树，而红黑树是一棵近似平衡的
二叉搜索树，即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证