Tires树数据结构

Posted 2022-12-06 JunMain

文章目录

• Tries
• • 什么是Tries树
  • 例如
  • Trie字符串统计
  • • • 题目描述
      • 输入格式
      • 输出格式
      • 数据范围
      • 输入样例：
      • 输出样例：
      • 题解
      • 代码
  • 最大异或对
  • • • 题目描述
      • 输入格式
      • 输出格式
      • 数据范围
      • 输入样例：
      • 输出样例：
      • 题解
      • 代码

Tries

什么是Tries树

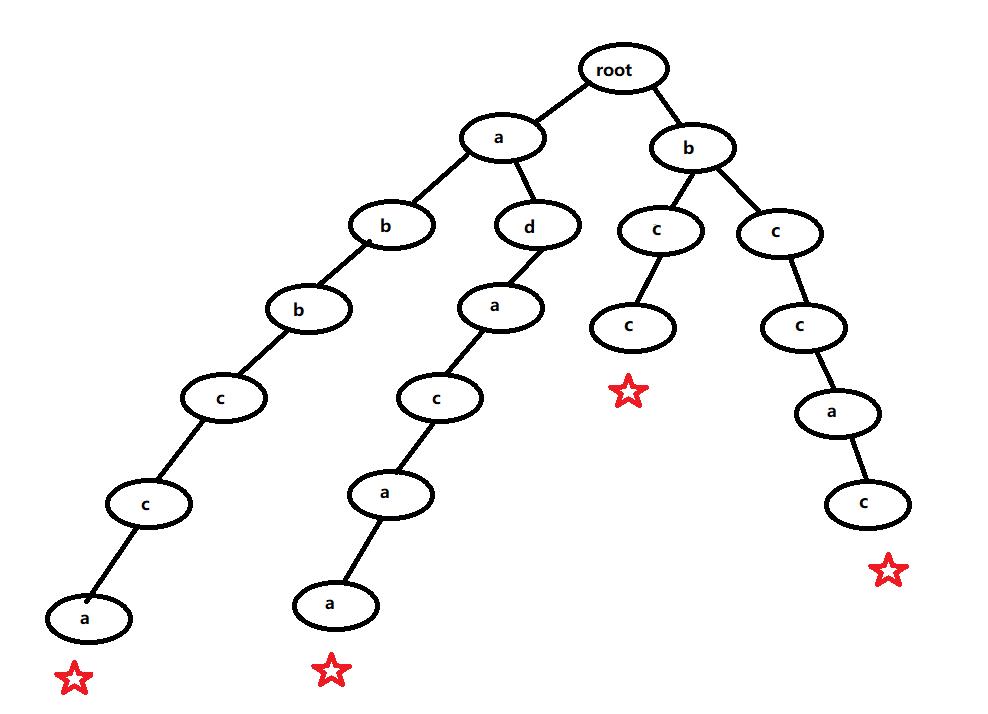
Tries树是用来高效的 存储、查找字符串集合的数据结构

例如

下面五个字符串的Tries如下
abbcca
adacaa
bcc
bccac

并且将每个字符结尾单词节点标记一下（表示存在已该点结尾的单词）

可以高效的查找一个字符串是否再集合中出现，与出现的次数
例如
查找	“bcc”
root -> b -> c -> c(有标记查找成功)

查找	“abbc”
root -> a -> b -> b -> c	(此处c节点没有标记， 不存在以c结尾的单词)	

Trie字符串统计

题目描述

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。
共有 N 个操作，输入的字符串总长度不超过 105，字符串仅包含小写英文字母。

输入格式

第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围

$1\le N\le 2\ast 10^4$

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

题解

Tries树的创建与查找关键是 两个函数以及， $son[N][26],idx,cnt[N]$这三个变量

$s[i][j]$ 的含义当前第i节点的儿子节点且存储的是第j个字母，的节点地址（理解为地址）

$cnt[i]$ 第i个节点中的单词作为结尾出现的次数（）

$idx$ 创建新的节点下标(创建新的模拟地址， 理解相当于new一个地址)

注意：root节点 == 0 为空

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 10010;

int son[N][26], idx, cnt[N];

void insert(char str[])

    int p = 0;
    for (int i = 0; str[i]; i ++)
    
        int u = str[i] - 'a';				//获取字母映射
        if (!son[p][u]) son[p][u] = ++ idx;     //如果是地址下标空的代表没有创建过， 防止重复创建
        p = son[p][u];							// p作为遍历指针， 指向刚才创建的儿子节点
    

    cnt[p] ++;				//标记最后单词结尾的节点	p是指针


int query(char str[])

    int p = 0;
    for (int i = 0; str[i]; i ++)
    
        int u = str[i] - 'a';
        if (!son[p][u])     return 0;	//如果当前p指向的儿子节点中没有改字母 则字符串不存在
        p = son[p][u];		
    

    return cnt[p];

int main()

    int n;
    cin >> n;

    while (n -- )
    
        char op[2], str[N];
        scanf("%s%s",op, str);
        if (op[0] == 'I')  insert(str);
        else    printf("%d\\n", query(str));
    
    return 0;

最大异或对

题目描述

在给定的 N 个整数 $A_1，A_2\dots \dots ,A_N$ 中选出两个进行 xor（异或）运算，得到的结果最大是多少？

输入格式

第一行输入一个整数 N。

第二行输入 N 个整数 $A_1～A_N$。

输出格式

输出一个整数表示答案。

数据范围

$1\le N\le 10^5,$
$0\le A_i<2^{31}$

输入样例：

3
1 2 3

输出样例：

3

题解

首先暴力做法$O(n^2)$

for (int i = 0; i < n; i ++)
    for (int j = 0; j <= i; i++)
    
        ans = max(ans,a[i] ^ a[j])
    

我们想办法优化内层循环

内层循环的含义：找到一个数与$a[i]$异或值最大

首先异或值最大，即从最高位开始，二进制位数相异， 每一位都如此最后找到的数字一定能是，异或a[i]最大的数字

我们把一个数字转化成二进制之后，用Tries树存下来

查找的时候用res记录查找的对应的十进制

优化过后内层从$O(n)$的时间复杂度变成了常数级别的了最坏$O(31)$

总的复杂度接近于$O(nlo{g}_n)$

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;

int son[N*31][2], idx;
int a[N];

void insert(int x)

    int p = 0;
    for (int i = 30; i >= 0; i --)
    
        int u = x >> i & 1;
        if (!son[p][u])     son[p][u] = ++ idx;
        p = son[p][u];
    


int query(int x)

    int p = 0, res = 0;
    for (int i = 30; i >= 0; i --)
    
        int u = x >> i & 1;
        if (son[p][!u])         //异或要找不同位数的、先判断该节点儿子节点!u是否存在
        
            res = res * 2 + !u;
            p = son[p][!u];
        
        else
        
            res = res * 2 + u;
            p = son[p][u];
        
    
    
    return res ^ x;

int main()

   int n, ans = 0;
   cin >> n;
   
   for (int i = 0; i < n;  i++)     scanf("%d", &a[i]);
   
   for (int i = 0; i < n; i ++)
   
       insert(a[i]);
       ans = max(ans,query(a[i]));
   
    
    cout << ans;
    return 0;